住宅价格的长记忆波动率特性实证分析
戴颖杰, 谢 燕, 冯照桢
(1. 西安交通大学 经济与金融学院, 陕西 西安 710061; 2. 中华全国工商业联合会 法律部, 北京 100035; 3. 中国人民银行 东莞分行, 广东 东莞 523000)
一、 问题的提出
LaCour-Little 等(2002)[1]指出房地产价格的波动对于资产风险管理、投资组合管理及银行的抵押贷款管理都有着至关重要的影响,科学地测度房地产价格波动给金融系统及整个宏观经济带来的风险,防范类似美国房地产市场的崩溃对全球金融稳定造成的巨大影响显得十分重要与迫切。Nelson(1990)发现,对于大多数金融资产,其条件方差往往体现出持续高度相关关系,而标准的GARCH模型则无法恰当地揭示这一特性[2]。这些模型在股票市场、债券市场及期货市场中得到了较为广泛的应用。但是,对于住宅价格的长记忆波动率特性的研究则十分少见[3]。目前,国内尚未发现对住宅价格的长记忆波动率特性的研究。因而,期望通过本文的研究填补国内这一空白。
Dolde & Tirtiroglu(1997) 对美国康涅狄格和旧金山地区的房价波动率进行了实证分析,发现存在明显的聚集效应[4]。Crawford & Fratantoni (2003) 也发现美国加利福尼亚、弗罗里达、马萨诸塞、俄亥俄和德克萨斯等州的房价波动率存在GARCH效应[5]。Miller& Peng (2006)对美国277个大中城市的房价进行了GARCH效应分析,发现17%的城市房价存在显著的GARCH效应。然而,以上实证分析都没有考虑房价的长记忆性问题[6]。
国内对于资产价格波动率长记忆特征的研究虽然比较多见,但绝大多数的研究主要围绕股票市场展开。陈梦根对股市中价格指数和个股日收益率的波动性进行分析后发现,少数个股存在长记忆性[7]。罗登跃和王玉华(2005)运用ARFIMA-FIGARCH模型对上证综合指数的波动率的长记忆特性进行了实证分析,发现其波动率过程具有显著的长记忆特性[8]。刘金全、郑挺国和隋建利分别运用ARFIMA-FIGARCH模型对我国通货膨胀率的均值过程和波动率过程的长期记忆行为进行了分析,发现通货膨胀率水平表现出长期记忆性行为[9]。耿克红和张世英提出了长记忆随机条件持续期模型(LMSCD),并针对中国股市超高频持续期序列进行了实证分析,发现中国股票市场存在长记忆性[10]。本文将对住宅价格是否存在长记忆波动率特性进行实证分析,以期对我国房地产宏观调控及房价的研究提供参考和依据。
二、 住宅价格长记忆波动率计量模型的构建
长记忆波动是指冲击对波动的缓慢衰减效应,这种现象可以通过波动指示性变量的自相关函数加以识别。本文通过住宅价格长记忆波动率模型来考察住宅市场的长期记忆特性,从而回答人们非常感兴趣的问题:我国住宅市场是否是有效市场,是否具有长记忆性?长记忆波动率特性有多强?
1. 模型ARCH效应及长记忆检验方法
一个平稳的时间序列如果具有长记忆特性,那么它的自回归函数就会衰减得很慢。这一点可以从时间序列自回归函数的特性中发现。当某一时间序列具有长记忆特性时,它的自回归函数为ρ(k)→Cρk-α,当k→∞,Cρ是一个正常数,0<α<1。从自回归函数可以发现,其按照双曲率衰减而不是按照指数形式衰减,衰减速率较慢。从时间序列的谱密度函数也可以得出类似的结论。具有长记忆特性的时间序列其自回归函数的谱密度函数如下:
f(w)=12π∑∞k=-∞ρ(k)eikw
(1)
当w→0时,f(w)→Cfwα-1,其中Cf为正常数,w为傅立叶频率。当频率等于零的时候,自回归函数的谱密度函数区域无穷大。因而,即使时间序列是平稳的,但是不能保证其自回归函数以指数形式快速衰减,序列时间仍存在长期“惯性”。但是,传统的时间序列计量方法无法解释时间序列的这一特征。
在分析一个时间序列是否具有长记忆特性和波动率聚集效应之前,应首先进行ARCH效应和长记忆效应检验。如果ARCH效应在统计上是显著的,则可以建立一个波动率方程,并对均值方程和波动率方程进行联合估计。对于长记忆效应,本文分别运用R/S检验和修正的R/S检验。R/S统计量和修正的R/S统计量分别如下:
QT=1STmax1≤k≤T∑kj=1(yi-y°)-min1≤k≤T∑kj=1(yi-y°)
(2)
其中y°=1T∑Ti=1yi;ST=1T∑Ti=1(yi-y°)2,yi如果是独立的且服从正态分布,那么1TQT⟹V,V是服从布朗桥运动的随机变量。当yi不是独立分布存在弱相关性,此时R/S统计量修正为:
T=1σ°T(q)×
max1≤k≤T∑kj=1(yi-y°)-min1≤k≤T∑kj=1(yi-y°)
(3)
2. 住宅价格长记忆波动率计量模型构建:FIGARCH模型
FIGARCH模型和一般的GARCH模型总体结构类似,由两个方程组成,一是均值方程,一是波动率方程。均值方程如下:
(4)
其中,yt为住宅价格的收益率;εt为白噪声随机项;Xt为k×1外生解释变量向量;θt为k×1相关系数向量。这一均值方程涵括了自回归AR、移动平均MA及自回归移动平均ARMA模型过程。FIGARCH模型和一般的GARCH的主要差别在波动率方程。FIGARCH模型的波动率方程结构如下:
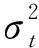
(5)
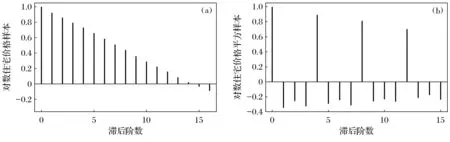
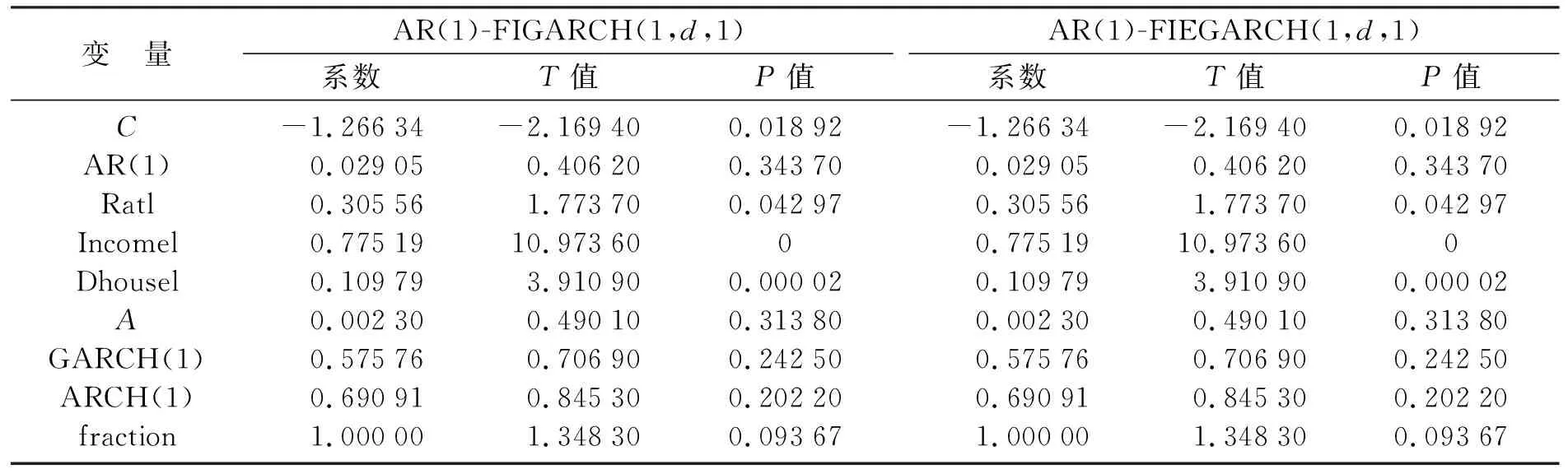
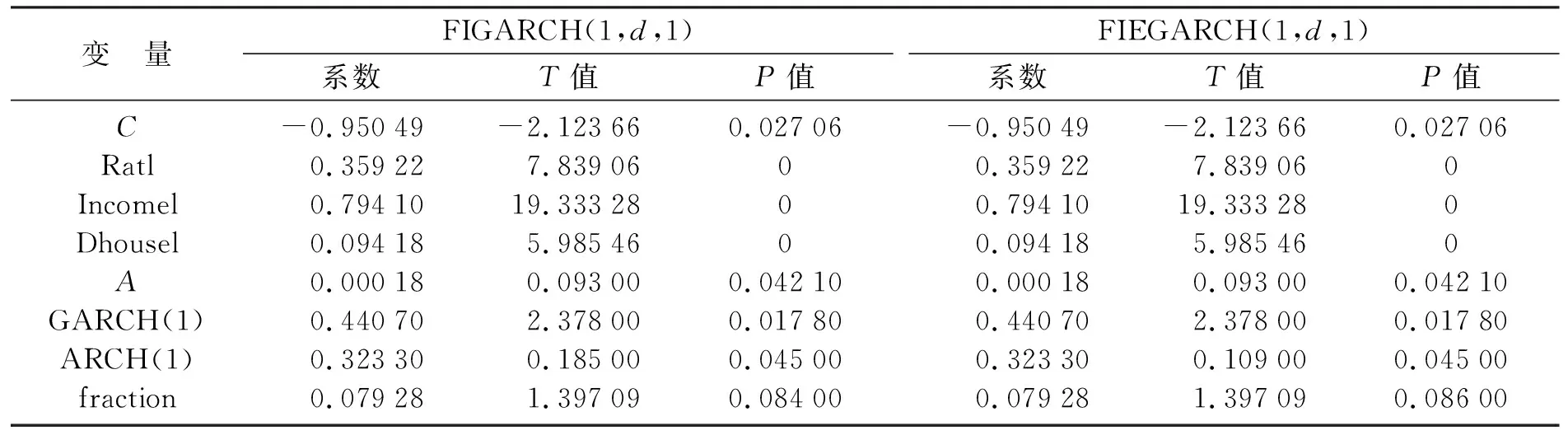
其中:Φ(L)=1-φ1L-φ2L2-…φmLm;b(L)=1-b1L-b2L2-…bqLq;d为分数滞后阶数也称理论滞后阶数,且0 建立FIGARCH模型,首先需要对均值方程的残差进行ARCH效应检验。如果均值方程不存在ARCH效应,那么就没有必要建立GARCH模型。对于住宅价格的均值方程,本文采用一个应用较多的标准房价方程,该方程的形式如下: ph=g(H/POP,Y,V,D) (6) 其中,V=r+δ-phe/ph;r、δ、phe、ph、H、POP及D分别代表利率、持有房产的税费率、房价预期、房价、房屋存量、城镇人口及房屋需求[11]。由于我国尚未开征物业税,房屋实际持有成本较低,可不考虑δ的影响[12]。预期房价很难测量,本文用住宅价格的滞后期作为预期房价的代理变量,这一点与梁云芳和高铁梅(2007)一文有所不同[13]。由于城镇人均可支配收入已经暗含城镇人口的信息,故而本文不单独考虑城镇人口对住宅价格的影响。另外,由于住宅存量数据的不可获得,同时为了反映住宅供给对住宅价格的影响,本文用当期住宅供给减去当期住宅销售作为住宅存量的代理变量。根据以上分析,在对以上变量取对数之后,住宅价格的具体均值方程如下: β4lnht+β5lnrt+εt (7) 本文所用数据主要来源于2000年以后的《中国经济景气月报》以及各年度《中国统计年鉴》,部分来源于国家统计局网站、中经网数据库等。所有数据均为季节性时间序列数据,跨度从2000年第一季度到2009年第四季度。本文在进行模型分析前对数据经过以下步骤处理:第一,季节性调整,消除季节性波动的影响;第二,消除价格因素的影响。 (1) ARCH效应及长记忆检验 首先,可以根据住宅价格时间序列的样本自相关图和对数住宅价格平方样本自相关图对住宅价格的ARCH效应作初步的描述性检验。其结果如图1所示。 从图1a可以看出,住宅价格取对数后的样本自相关系数在滞后9阶以后落入一倍标准差内,体现出对数住宅价格是平稳数列。但是,从图1b明显可以发现,对数住宅价格的平方的自相关系数有明显的聚集现象,另外在滞后9阶以后仍旧没有收敛在一倍标准差范围以内。对比图1a和图1b初步可以判定对数住宅价格存在ARCH效应。 图1 对数住宅价格时间序列样本相关图及平方样本自相关图(a)—对数住宅价格样本; (b)—对数住宅价格平方样本 然后,本文运用Splus 8.0软件,对住宅价格的ARCH效应和长记忆效应检验进行统计检验。具体检验结果见表1。 表1 ARCH效应和长记忆效应检验结果 注: *、**分别表示在0.05、0.01水平上显著。 从ARCH效应及长记忆效应的检验结果来看,在5%的显著水平下ARCH效应的检验统计值为27.941 1,大于21.03,拒绝了住宅价格均值方程没有ARCH效应的原假设。这说明住宅价格建立ARCH模型是可行的。根据R/S和修正的R/S检验结果来看,不管在5%的显著水平还是在1%的显著水平下,均说明住宅价格存在长记忆效应。通过这两种检验说明,对住宅价格建立长记忆波动率模型是具备可行性的。 (2) 住宅价格FIGARCH模型估计结果 本文首先在AR(p)模型的基础上,根据AIC信息准则对均值方程中住宅价格的滞后期进行定阶。然后,再建立AR-FIGARCH(p,d,q),并对其估计比较,从而选择较为合适的FIGARCH模型。 根据表2可以看出,住宅价格滞后两阶时,AIC值最小。因而,本文分别估计AR(1)-FIGARCH(1,d,1)模型和AR(1)-FIEGARCH(1,d,1)模型,以便在这两个模型中选择较优的一个。这两个模型的估计结果见表3。 表2 均值方程滞后阶数的确定 注: 在Splus 8.0软件中,AIC最小的值设置为0。 表3 AR(1)-FIGARCH(1,d,1)和AR(1)-FIEGARCH(1,d,1)估计结果 [注:C和A为常数项;Ratl 、Incomel 、Dhousel为均值方程的解释变量,分别代表利率、收入和住宅;AR(1)为一阶滞后相关性;GARCH(1)为广义自回归条件异方差模型;ARCH(1)为自回归条件异方差模型;fraction为理论差分系数。 从表3所示的模型估计结果来看:第一,AR(1)-FIGARCH(1,d,1)模型估计的结果和AR(1)-FIEGARCH(1,d,1)模型估计的结果几乎没有差异;第二,这两个模型估计的系数,除了均值方程中常数项(C)及外生解释变量的系数在5%的显著性水平下显著外,其他系数并不显著;第三,根据以上两个模型的估计结果,理论差分系数d(fraction)=1,但是统计值并不显著。综上,以上建立的这两个模型设定不当,需进一步改进修正。 根据模型简化性原则,本文首先剔除均值方程中住宅价格的滞后项,将利率、收入和住宅需求作为均值方程的解释变量,然后再分别估计比较FIGARCH(1,d,1)模型和FIEGARCH(1,d,1)模型。 从表4可以发现:第一,FIGARCH模型和FIEGARCH模型估计结果几乎没有差异;第二,均值方程及波动率方程的系数均在5%的显著性水平下显著,所有系数的P值都小于0.1;第三,从波动率方程的系数来看,GARCH(1)和ARCH(1)系数之和为0.764<1,说明波动率方程稳定;第四,理论差分系数d(fraction)小于0.5,即0 表4 FIGARCH(1,d,1)和FIEGARCH(1,d,1)估计结果 [注:C和A为常数项;Ratl 、Incomel 、Dhousel为均值方程的解释变量,分别代表利率、收入和住宅;AR(1)为一阶滞后相关性;GARCH(1)为广义自回归条件异方差模型;ARCH(1)为自回归条件异方差模型;fraction为理论差分系数。 本文利用2000年第一季度到2009年第四季度的数据,对我国商品住宅价格的波动率特性进行了实证分析,对我国住宅价格及其调控有以下几点启示和建议: 我国商品住宅价格具有长记忆波动率的特性说明,我国的住宅市场并非有效的市场。目前有效市场假说前提下的资产定价是研究住宅价格的主流研究方法之一,那么根据本文的实证分析结果,这种主流研究方法存在根本的缺陷,对于商品住宅价格的研究应当注重市场主体的非理性行为对住宅价格的影响。 人均可支配收入对住宅价格有一定影响,支持了国内外对于房价影响因素的相关性研究。但是根据FIGARCH和FIEGARCH模型均值方程中人均收入的系数可以发现,住宅价格对人均可支配收入的弹性系数约为0.79,弹性系数小于1。弹性系数小于1说明住宅价格对人均可支配收入缺乏弹性,进而在一定程度上证实了住宅价格脱离了居民可支付能力,住宅价格存在一定程度的泡沫。 目前运用利率对住宅价格进行调控的效果其实并不理想。2004年10月28日、2005年7月21日及2006年4月27日,央行提高利率以后,房地产价格并没有出现下降,反而出现了当期房地产价格上涨的异常现象。笔者认为,这与住宅具有投资属性有关,住宅价格的波动具有长记忆性,相对于其他资产而言短期收益率较高,进而引致投资资金流向房地产,从而推动了住宅的投资性需求,进而导致住宅价格的上升。所以建议对住宅价格的调控应当更加注重数量型工具,价格性调控工具实际效果往往会适得其反。 对于目前商品住宅价格的调控而言,应当注重政策的稳定性和长期性,因为政策在短期内无法对商品住宅价格作出有效的调控,而这一点过去没有引起调控当局的足够重视。2008年9月以前,国家对房价的调控以稳定房价为主要目标,而2008年9月至2009年11月,政策又以刺激房地产需求,鼓励和推动房地产业为导向,2009年11月后政策又以抑制房价过快上涨为目标。在某种程度上讲,国家对房价调控的效果不理想的部分原因就在于政策缺乏连续性,没有注重政策的稳定性和长期性。 资产回报的波动是影响VAR测度的主要因素之一,在度量VAR值时候不仅要注意资产回报的波动存在异方差性[14],而且更要注意到市场冲击对回报的条件方差有着持续性影响, 回报的波动具有长期记忆性[15]。住宅价格波动的聚集效应和长记忆性说明,住宅价格的风险具有异质性,并非长期稳定不变。因而,在同方差假定条件下对住宅价格风险进行的评估是不科学的,在一定程度上降低了对住宅价格风险的评估,所以金融机构应当不定期地对房产信贷风险作出评估。 参考文献: [1][LaCour-Little M, Marschoun M, Maxam C. Improving Parametric Mortgage Prepayment Models with Non-Parametric Kernel Regression[J]. Journal of Real Estate Research, 2002,24:299-328. [2][Nelson D. Stationarity and Persistence in the GARCH(1, 1) Model[J]. Econometric Theory, 1990,6:318-334. [3][Miles W. Long-range Dependence in U.S. Home Price Volatility[J]. Journal of Real Finance and Economics, 2011,42:329-347. [4][Dolde W, Tirtiroglu D. Temporal and Spatial Information Diffusion in Real Estate Price Changes and Variances[J]. Real Estate Economics, 1997,25:539-565. [5][Crawford G, Fratantoni M. Assessing the Forecasting Performance of Regime-switching ARIMA and GARCH Models of House Prices[J]. Real Estate Economics, 2003,31:223-243. [6][Miller N, Peng L. Exploring Metropolitan Housing Price Volatility[J]. Journal of Real Estate Finance and Economics, 2006,37:5-18. [7][陈梦根. 中国股市的长期记忆效益实证研究[J]. 经济研究, 2003(3):70-78. [8][罗登跃,王玉华. 上海股市收益率和波动性长记忆特征实证研究[J]. 金融研究, 2005(11):65-66. [9][刘金全,郑挺国,隋建利. 我国通货膨胀率均值过程和波动过程中的双长记忆性度量与统计检验[J]. 管理世界, 2007(7):14-21. [10][耿克红,张世英. 中国股市超高频持续期序列长记忆性研究[J]. 中国管理科学, 2008(2):7-13. [11][Stevenson S. Modeling Housing Market Fundamentals: Empirical Evidence of Extreme Market Conditions[J]. Real Estate Economics, 2008,36:1-2. [12][余华义. 经济基本面还是房地产政策在影响中国的房价[J]. 财贸经济, 2010(3):116-122. [13][梁云芳,高铁梅. 中国房地产价格波动区域差异的实证分析[J]. 经济研究, 2007(8):35-37. [14][Alexander J M, Rudiger F. Estimation of Tail- related Risk Measures for Heteroscedastic Financial Time Series: An Extreme Value Approach[J]. Journal of Empirical Finance, 2000,3(7):271-300. [15][Ping T W,Shwu J S. Value-at-risk Analysis for Long-term Interest Rate Futures: Fat-tail and Long Memory in Return Innovations[J]. Journal of Empirical Finance, 2007,10(14):248-259.3. 住宅价格均值方程
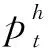
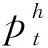
三、 实证分析
1. 数据来源及说明
2. 实证结果


四、 结论与对策
1. 我国的住宅市场并非有效的市场
2. 当前我国的住宅价格存在一定程度的泡沫
3. 对住宅价格的调控应当更加注重数量型工具
4. 注重政策的稳定性和长期性
5. 金融机构应当不定期地对房产信贷风险作出评估

