不同车流对桥梁静三分力及局部风压影响的风洞试验研究*
韩艳,刘书倩,宋奎,蔡春声,2,何旭辉
(1.长沙理工大学桥梁工程安全控制省部共建教育部重点实验室,湖南长沙 410114;2.美国路易斯安那州立大学土木与环境工程,美国路易斯安那州,巴吞鲁日 70803;3.中南大学土木工程学院,湖南 长沙 410075)
我国目前已经修建和正在修建的跨深山峡谷和海峡的桥梁越来越多,桥梁结构向大跨径,轻柔化发展,对风的敏感性愈发突出;此外,随着国民经济的快速增长,桥上行驶车辆不断增加,速度不断提高,大量车辆在桥梁上的行驶改变了桥梁的局部动力特性,风-车-桥系统的耦合响应更为突出。因此,准确预测风—车—桥耦合系统的桥梁风致响应和评价车辆安全、舒适性至关重要。风-车-桥系统的气动特性的准确测量是预测风—车—桥耦合系统风致响应的前提。目前越来越多的学者在研究车辆和桥梁间的相互气动影响。葛玉梅等[1]通过节段模型风洞试验测试了有静止车辆的桥梁断面和列车的气动参数,研究了静止列车和桥梁间相互气动影响。李永乐等[4]等采用交叉滑槽系统,通过组合节段模型试验分别测试了车-桥系统中车辆和桥梁的气动力,并利用线性结构气动力的余弦规则来考虑车辆运动对气动力的影响。李永乐[4]等还研究了车辆和车道间的相对几何关系对车辆和桥梁的气动特性影响。韩艳等[5-7]采用数值计算方法和风洞试验对风-车-桥耦合系统的车辆和桥梁气动特性进行了研究,分析了静止车辆对桥梁静气动力的影响以及风场的紊流性对车桥静气动力的影响。以上研究虽然都考虑了个别车辆与桥梁间的相互气动影响,但在实际运营状况中,公路桥梁车流荷载具有较强的随机性,受时间、环境及地方经济等众多因素影响。为了考虑实际运营状态下随机车辆对桥梁断面气动力的影响,本文模拟了4种不同车流状态,分别研究了不同车流下车辆对桥梁断面三分力以及局部风压的影响,以便为以后车辆对桥梁三分力影响的修正系数的提供便利。
1 风洞试验简介
1.1 试验测试模型与装置
模型缩尺比为1∶60,为了方便测压点的布置,桥梁节段模型由有机玻璃板制作而成,长度为1.54 m,如图1所示。选用2种典型的车型(小轿车和大型客车),如图2所示。将模型悬挂于湖南大学开发的强迫振动置上,同时可以利用该装置测试无车时桥梁断面的三分力,风洞中悬挂模型的测试装置示意图如图3所示。

图1 桥梁节段模型断面示意图Fig.1 Bridge model geometry and overall dimensions
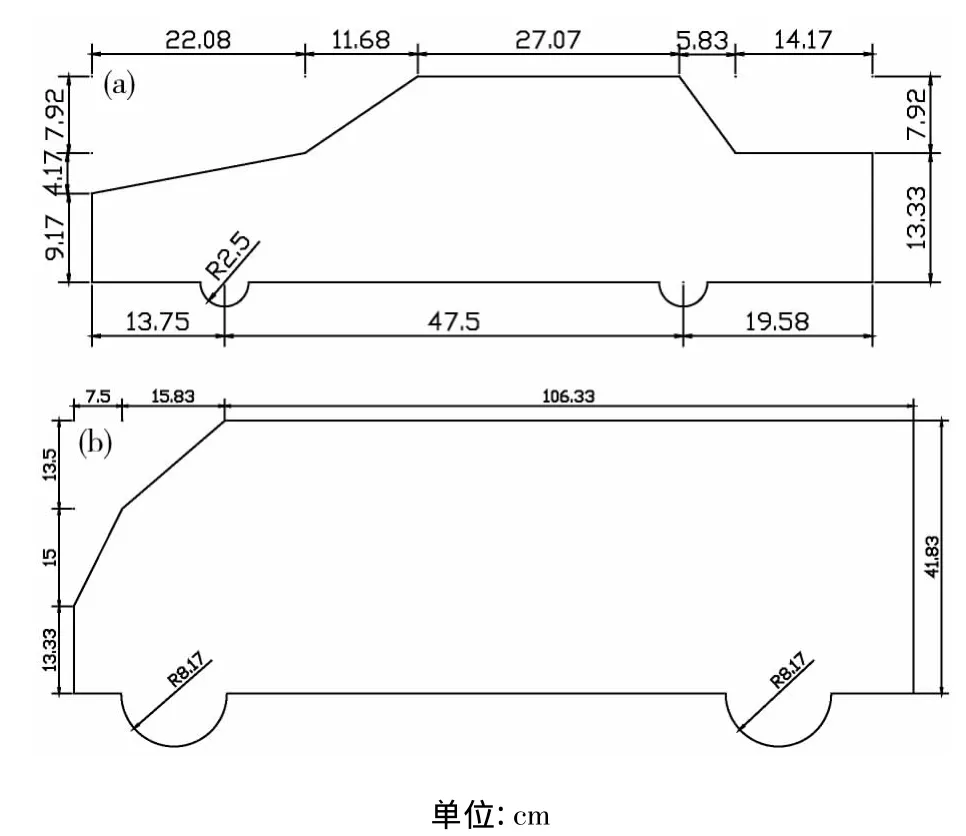
图2 两种车辆的外形示意图Fig.2 Vehicle models geometry and overall dimensions

图3 风洞中悬挂模型的测试装置示意图Fig.3 Experimental device with testing model in wind tunnel
1.2 测试断面及测孔布置
为了分离测试桥梁和车辆的气动力,采用测压法测试桥梁的气动力。另外,为了验证测压法的正确性,分别采用测力法和测压法测试了桥上无车时的桥梁断面气动力。桥梁测试模型共布置8个测压断面(A-H断面),每个断面布置54个测孔,如图4所示。
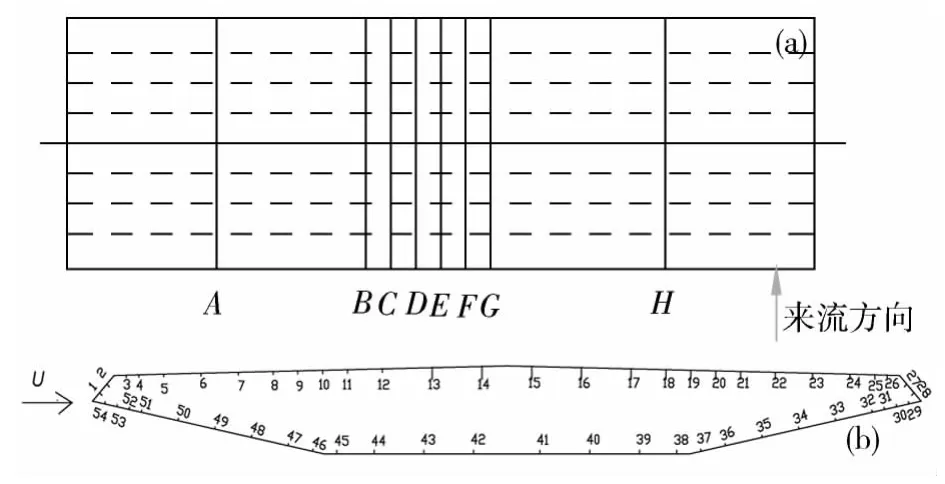
图4 桥梁节段模型测压断面与测压孔布置示意图Fig.4 Layout of the measuring sections and pressure points on measuring sections
1.3 不同车流模拟与测试工况
为了考虑不同车流对桥梁断面气动力的影响,模拟了4种交通状况即自由行驶状态、中等繁忙状态、繁忙状态和堵车状态。由于实验条件以及测点布置等因素的局限,难以完全模拟实际状况中的随机车流状况,各种交通状态的车辆布置如图5所示。针对这4种交通状态,分别测试了-6°,-4°,-2°,0°,2°,4°和 6°攻角下的桥梁断面表面风压,具体的测试工况如表1所示。
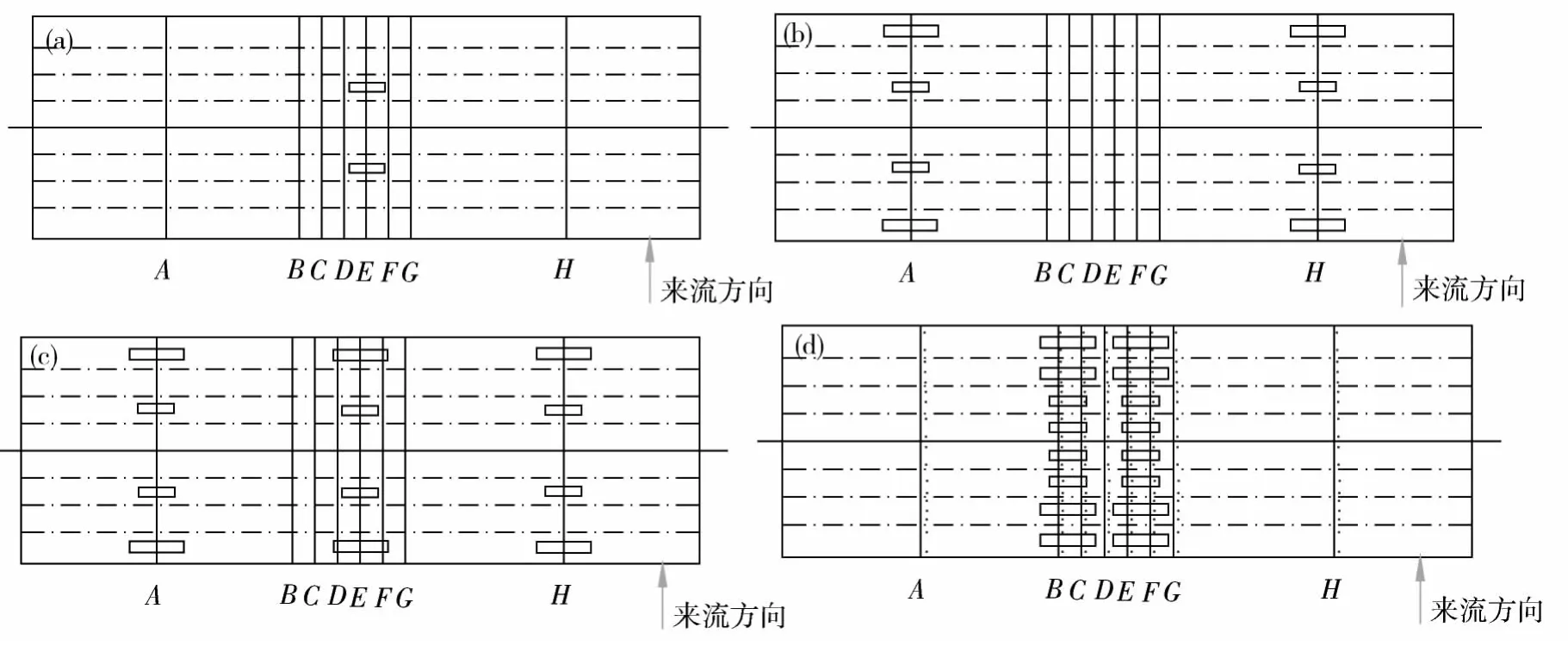
图5 4种交通状态下车辆布置示意图Fig.5 Vehicle arrangement under four kinds of traffic condition

表1 测试工况Table 1 Test conditions
对于桥上无车情况下,桥梁断面的气动力分别通过测力法和测压法测量得到,对于4种交通状态下,桥梁断面的气动力通过测压法测量得到。采用测压法时,通过积分得到每个桥梁断面的体轴坐标系下的气动力为:

其中:FHj,FVj和Mj分别为第j断面体轴坐标系下作用于断面形心的阻力、升力和升力矩,其方向如图6所示;¯pij为第j断面上第i测点的压力平均值;ΔLij为第j断面上第i测点的压力积分长度;θij为第j断面上第i测点的压力与体轴竖向坐标的夹角,其正方向如图6所示;dHij和dVij分别为第j断面上第i测点的正阻力分量对截面形心的力臂和正升力分量对截面形心的力臂。
测力法得到的气动力是风轴坐标系下的气动力,而测压法得到的气动力是体轴坐标系下的气动力,为了使得两种方法的结果统一,将体轴坐标系下的结果转化为风轴坐标系下的结果,转化公式为:

式中:Dj,Lj和Mj分别为风轴坐标系下作用于第i桥梁断面形心的阻力、升力和升力矩,其方向如图6所示;α为风攻角,如图6所示。
将每个桥梁断面的三分力沿桥长方向求和之后取平均即为该节段模型桥梁断面的三分力。由于实验条件的限制,无法测得每一个桥梁断面的三分力,故利用测得的A~H 7个断面的三分力根据就近相等原则近似计算作用于桥梁断面形心的阻力D、升力L和升力矩M,也就是靠近布车断面有效范围内按布车断面三分力求和,其余按无车断面三分力求和,然后,在考虑的模型长度上取平均。
计算桥梁断面三分力系数时,参考宽度取主梁断面宽度B,则桥梁断面气动力系数定义为:

式中:ρ为空气密度;U为平均风速度;α为风攻角;B为桥梁断面宽度;l为考虑的模型长度,对于无车和工况1~3,其为桥梁模型总长1.5 m,对于工况4,如果考虑的模型长度为模型总长,那么需要布置更多的测压断面,受试验条件限制,考虑的模型长度只能缩短,取中间布车影响的有效长度;CD,CL和CM分别为桥梁断面的阻力系数、升力系数和升力矩系数;D,L和M分别为风轴坐标系下作用于桥梁断面形心的阻力、升力和升力矩,其方向定义如图6所示。
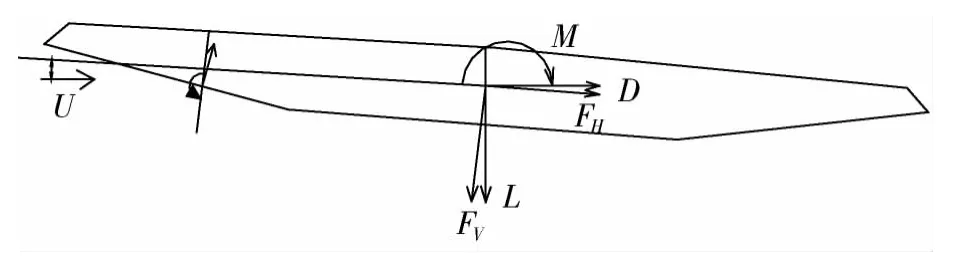
图6 风轴坐标系下桥梁断面气动力方向示意图Fig.6 The direction of the aerodynamic forces of bridge under wind axis coordinates
2 试验结果及分析
图7所示为桥上无车情况下分别采用测力法和测压法得到的桥梁断面三分力系数。从图7可看出:采用测压法和测力法得到的升力系数和升力矩系数吻合得较好,而测力法的阻力系数较测压法的系数要大。Ricciardelli等[8-9]等也曾尝试过用测力法和测压法来测定单幅桥面桥梁的三分力系数,发现2种方法测得的升力系数和升力矩系数吻合得较好;而阻力系数测压法得到的结果只是测力法结果的2/3左右,该误差是桥面栏杆等附属物上无法布置测压孔、压力积分阻力中不包括风对桥面栏杆等附属物的阻力造成的。测力法和测压法的风洞试验结果对比基本上说明了本试验结果的可靠性。
图8所示为5种工况下采用测压法得到的桥梁断面三分力系数。表2~4所示为不同工况下桥梁断面三分力系数及对比情况。从图8和表2~4可以看出:不同交通状态下车辆对桥梁断面三分力系数的影响程度不同,在堵车情况下,车辆对其影响最大,使阻力系数和升力矩系数显著减小,尤其在0°攻角时,使阻力系数减小了21%,使升力矩系数减小了11倍。在堵车情况下,车辆使升力系数增大,在2°攻角时,增加将近1倍。由此可见:在风-车-桥耦合振动分析中,车辆对桥梁气动力的影响不容忽视。

图7 桥上无车时桥梁断面的三分力系数Fig.7 Static aerodynamic coefficients of the bridge with no vehicle
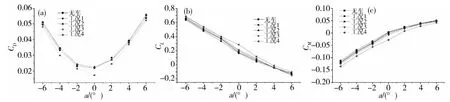
图8 不同工况下的桥梁断面三分力系数Fig.8 Static aerodynamic coefficients of the bridge under different traffic flows
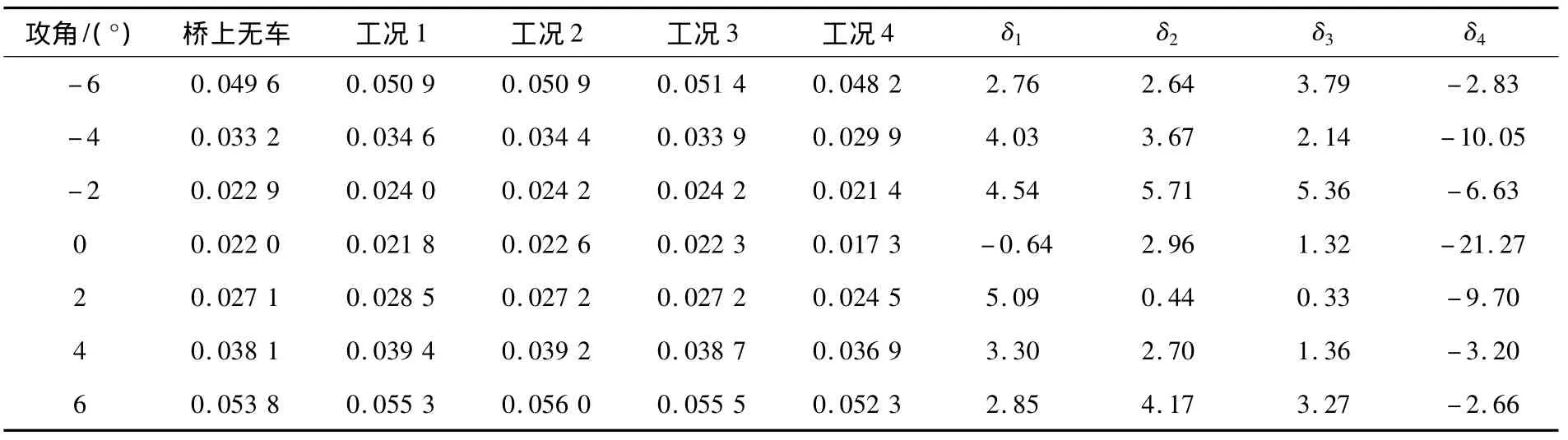
表2 阻力系数的对比情况Table 2 Drag coefficients in different cases

表3 升力系数的对比情况Table 3 Lift coefficients in different cases
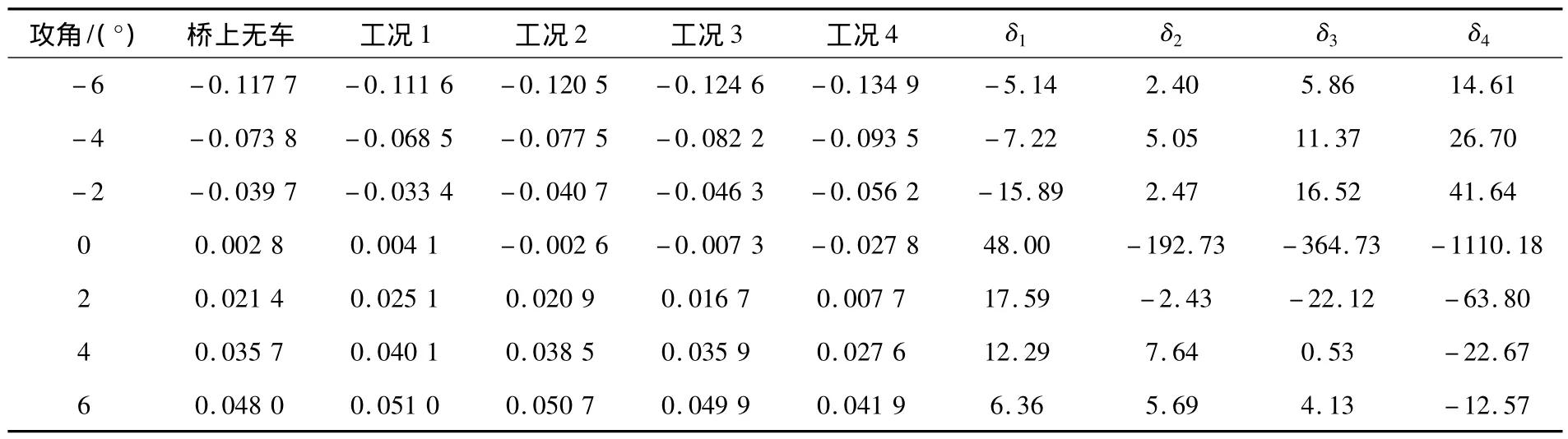
表4 升力矩系数的对比情况Table 4 Pitching moment coefficients in different cases
3 桥梁断面风压分布研究
利用测压法得到的数据,计算各个截面单个测点平均压力系数,计算公式为

其中:Ci和Pi分别为第i个测点的平均压力系数值和平均压强,ρ为空气密度,U为平均风速。
图9所示为桥梁典型断面测压点与车辆相对位置示意图。图10所示为0°,-6°和6°风攻角下的桥梁典型断面平均压力系数分布图,其中平均压力系数以指向桥面外侧为负,内侧为正。考虑到平均压力系数远小于实际的桥梁断面尺寸,图10中的平均压力系数均乘了1 000的放大因子。
图10所示是4个典型断面分别为无车、工况1的E断面(布置2辆车)、工况2的A断面(布置4辆车)、工况4的B断面(布置8辆车)。由图10可知:风攻角、桥上无车和有车以及车辆数量和车辆位置对断面测点压力值均有不同程度的影响。
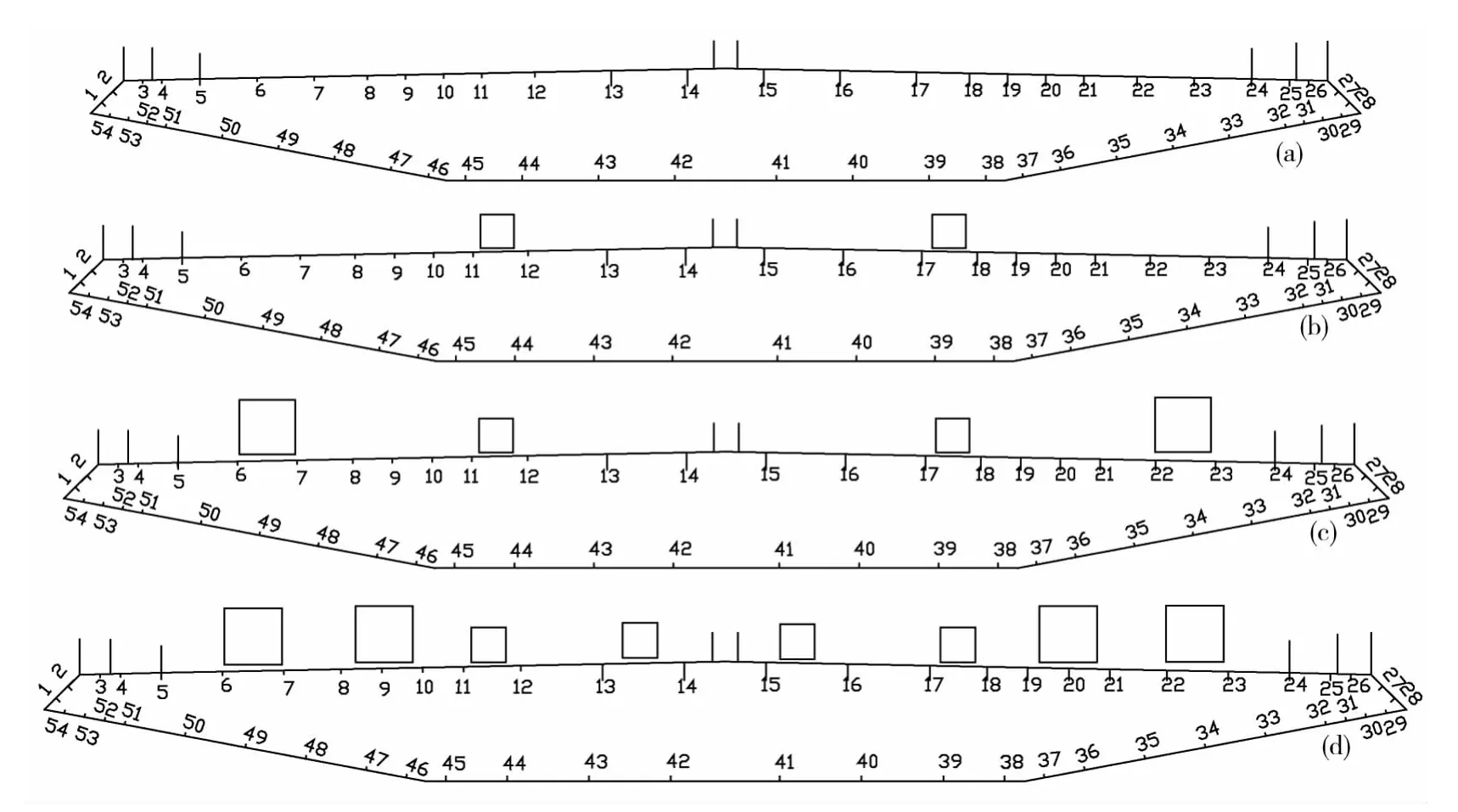
图9 桥梁典型断面测压点与车辆相对位置示意图Fig.9 The relative position of the vehicle and pressure points on typical bridge scetions
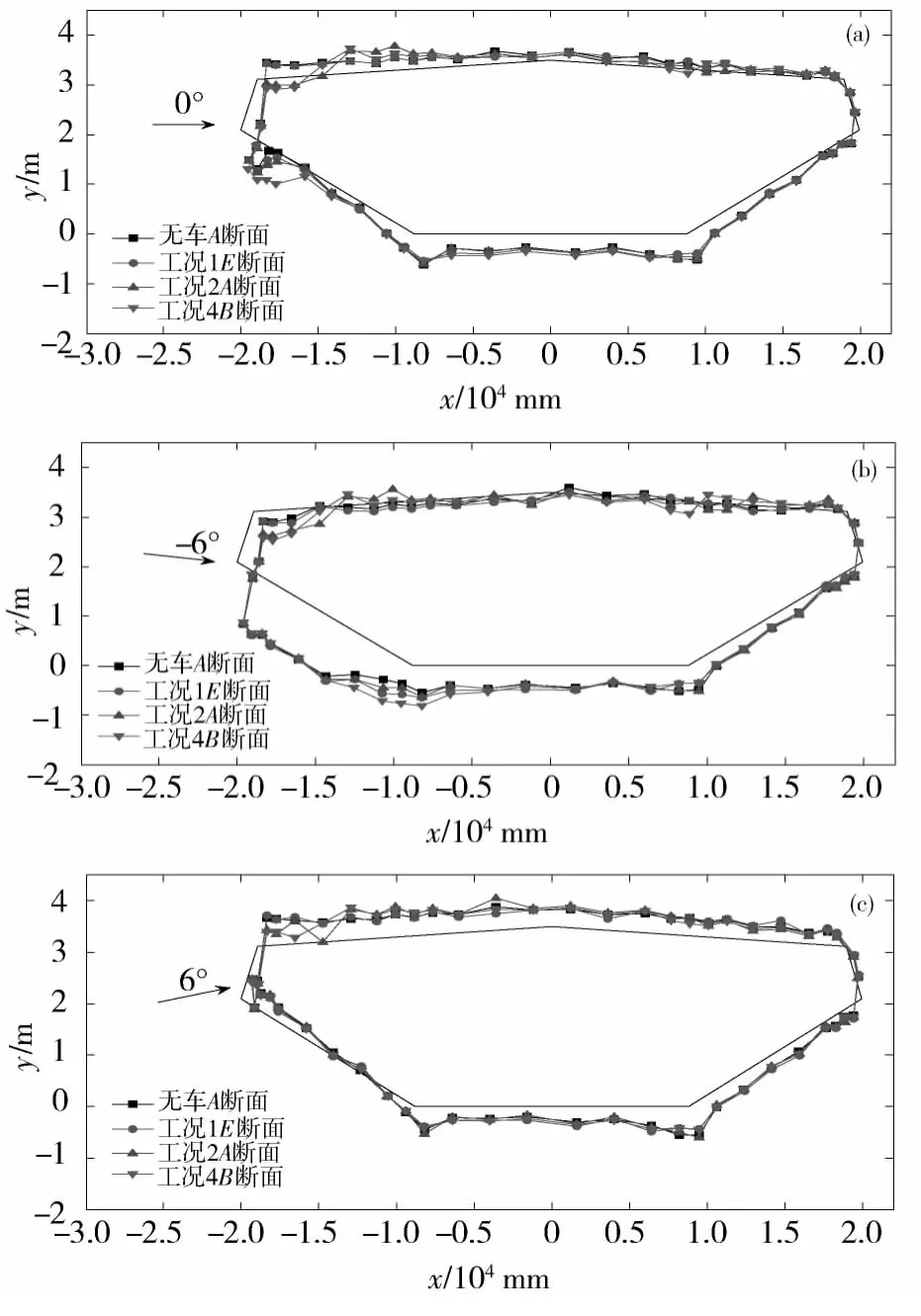
图10 桥梁典型断面压力系数均值图Fig.10 The mean pressure coefficient of bridge section
在0°风攻角时,无车A断面和工况1E断面顶面测点压力值为负,即测点受拉力,且由迎风侧到背风侧压力值绝对值略有减小。由于工况1E断面车辆布置较少,且相距较远,风车桥耦合效应不明显,车辆对风基本不产生阻碍作用,故此时工况1E断面的压力分布与无车时基本一致。而此时工况2A断面与工况4B断面由于车辆布置较多较密,对顶面迎风侧压力影响较大。由于车体的阻挡,风在车辆底部流动受阻,在车体迎风面一侧的区域短暂聚集并沿车体向上爬升,并在车底形成负压区,故风在流经车辆之前的压力为正值,在车辆处迅速由正变负且其绝对值略大于无车时的压力绝对值,随着距离的增大,车桥耦合风场作用减弱,压力绝对值又逐渐减小并接近无车时的压力绝对值。
在 -6°风攻角时,风对顶面的压力基本为正。迎风侧顶面压力与0°风攻角时比较均有不同程度的增大,无车A断面和工况1E断面顶面栏杆分布区更是由负压变为正压,幅值变化较大。这是由于0°风攻角时风在桥梁钝体断面迎风侧产生分离,而-6°风攻角时分离点上移,风压直接作用于迎风侧顶面致使该区域压力产生由负到正的剧烈变化。而工况2A断面和工况4B断面由于车辆的阻挡作用,在0°风攻角时与-在6°风攻角时比较迎风侧顶面压力略有增加,但相对无车A断面与工况1E断面变化较小。-6°风攻角时,在迎风侧下部形成了一个较大的负压区,且该区域负压与0°风攻角时比较急剧增大。在6°风攻角时,风在桥梁断面顶面形成一个负压区,故顶面压力均为负,且负值较大。迎风侧下部的压力由 -6°风攻角时的较大负压变为正压。
4 结论
(1)车辆的存在对桥梁气动特性影响显著,在不同交通状态下车辆对桥梁断面三分力系数及风压分布的影响程度不同。
(2)在不同交通状况下,车辆与桥道间以及不同行车位置的车辆间存在明显的气动干扰,桥梁断面迎风侧风压变化较大,而背风侧的影响不明显。而堵车时车辆对桥梁断面三分力系数影响最大,使阻力系数和升力矩系数显著减小,升力系数增大。
(3)在风—车—桥耦合振动分析中,不同交通状态对桥梁气动力及风压分布的影响不容忽略,故设计中应予以考虑,确保行车安全舒适。
[1]葛玉梅,李永乐,何向东.作用在车-桥系统上风荷载的风洞试验研究[J].西南交通大学学报,2001,36(6):612-616.GE Yumei,LI Yongle,HE Xiangdong.Study on wind -induced loads of train-bridge system by wind tunnel test[J].Journal of Southwest Jiaotong University,2001,36(6):612-616.
[2]李永乐,廖海黎,强士中.车桥系统气动特性的节段模型风洞实验研究[J].铁道学报,2004,26(3):71 -75.LI Yongle,LIAOHaili,QIANGShizhong.Study on aerodynamic characteristics of the vehicle-bridge system by the section model wind tunnel test[J].Journal of the China Railway Society,2004,26(3):71 -75.
[3]李永乐,胡明,张明金,等.侧向风作用下车-桥系统的气动特性-基于风洞试验的参数研究[J].西南交通大学学报,2012,47(2):210 -217.LI Yongle,HU Peng,ZHANG Mingjin,et al.Aerodynamic characteristics of vehicle-bridge system under cross wind:parameter studies based on wind tunnel test[J].Journal of Southwest Jiaotong University,2012,47(2):210-217.
[4]李永乐,周昱,葛世平,等.主梁断面形状对车-桥系统气动特性影响的风洞试验研究[J].土木工程学报,2012,45(7):135 -141.LI Yongle,ZHOU Yu,GE Shiping,et al.Wind tunnel test study of the effect of bridge deck cross section shape on aerodynamic characteristics of vehicle-bridge system[J].China Civil Engineering Journal,2012,45(7):135-141.
[5]韩艳,胡揭玄,蔡春声.横风作用下公路车辆与桥梁静气动力的数值模拟研究[J].铁道科学与工程学报,2012,9(1):12 -17.HAN Yan,HU Jiexuan,CAI Chunsheng.Numerical simulation on static aerodynamic forces of vehicles and bridges under cross winds[J].Journal of Railway Science and Engineering,2012,9(1):12-17.
[6]韩艳,胡揭玄,蔡春声,等.横风作用下考虑车辆运动的车桥气动特性的数值模拟研究[J].工程力学,2013,30(2):318-325.HAN Yan,HUJiexuan,CAIChunsheng,et al.Numersical simulation on aerodynamic characteristics of vehicles and bridges under cross wind with the consideration of vehicle moving[J].Engineering Mechanics,2013,30(2):318-325.
[7]YAN Han,Jiexuan Hu,Cai CS,et al.Experimental and numerical study of aerodynamic forces on vehicles and bridges[J].Wind and Structures,2013,17(2):001 -000 DOI:http://dx.doi.org/10.12989/was.2013.17.2.001.
[8]Ricciardelli F,Hangan H.Pressure distribution andaerodynamic forces on stationary box bridge sections[J].Wind and Structures,2001,4(5):399 -412.
[9]金挺,林志兴.扁平箱形桥梁断面斯特罗哈数的雷诺数效应研究[J].工程力学,2006(10):32.JING Ting,LIN Zhixing.Reynolds number effects on strouhal number of flat- box girder bridge decks[J].Engineering Mechanics,2006(10):32.
- 铁道科学与工程学报的其它文章
- 侧风下挡风墙对CRH2列车-简支梁桥气动性能的影响*

