生产线物料配送的路径优化研究
党立伟 孙小明
(上海交通大学机械与动力工程学院,上海 200240)
0 引言
自车辆路径问题被Dantzig[1]提出后,引起了国内外学者的重视。目前很多学者对带时间窗的多目标车辆路径问题[2-4]和带软时间窗的车辆路径问题[5-7]进行了研究,而有关生产线物料配送的研究比较少。Boysen[8]等研究了混流装配线的物料准时化配送。蒋丽[9]等提出以工位为中心的物料配送方案,即将物料按照工位的需求进行分类存储,并给出了车辆的配送方案。曹振新[10]等对混流装配生产线上的物料配送问题进行了研究,设计了总装车间的物料ANDON系统,在系统中设定了线旁物料的Max/Min值,当达到这个值时系统会自动报警,同时给出了物料断点的处理流程。本文研究了如何运用有限的配送车辆对生产线所需要的物料进行准时配送。
1 问题描述
设一条生产线由n个工位组成,每个工位的物料需求量为qi(i=1,2,…,n)。仓库拥有K辆容量相同的车,每辆车的容量为Q。每个工位的物料需求量不大于每辆车的容量,即qi≤Q,n个工位物料需求量之和大于K辆车的总容量,每工位所需要的物料被一辆车配送一次完成。车辆从同一仓库出发对各个工位所需要的物料进行配送,仓库与工位的距离矩阵为dij,车辆的行驶时间为t1,物料的装卸时间为t2。由于物料的总需求量大于车辆的总容量,因此车辆需要进行多次配送才能完成配送任务。配送目标是合理安排车辆服务的工位及行车路径,使物料配送的时间最短。
2 解决方案
2.1 单车辆的物料配送问题
首先研究单车辆的情况。因为只有一辆车,所以车辆总的装卸货时间是常数,求解的目标可转化为求车辆的最短行驶时间。一辆车要完成n个工位的物料配送,则最极端的情况是此辆车在工位和仓库之间往返n次完成物料配送,因此假定车次数是n。基于上述分析建立了如下的数学模型。
式中:k=1,2,…,n;1≤i≠j≤n。
式(3)表示目标函数,即总的配送时间包括车辆的行驶时间和物料的装卸时间;式(4)表示每个车次装的物料数量不能超过车辆的容量;式(5)表示每个工位只被一个车次服务;式(6)和式(7)表示车辆行驶的连续性;式(8)表示消除支路,保证车辆从仓库出发最后回到仓库;式(9)表示辅助变量。
本文采用商业优化软件Cplex对上述模型进行求解。
2.2 改进的遗传算法
对于多车辆的物料配送问题,总的配送时间就是所有车辆中配送时间的最大值,求解目标是使车辆的最大配送时间最小化。对此,本文提出了改进的遗传算法。首先将工位分配到车辆,分配的原则是每辆车运送的物料数量基本相同,则所需要的装卸货时间也就相同了,只需要对车辆的行驶时间进行优化即可,此问题就转化为了单车辆的物料配送问题。
2.2.1 初始解的生成本文运用自然数进行编码,具体的编码过程如下。①根据每辆车配送物料数量基本相同的原则,将工位分配给车辆。
②将每辆车所服务的工位代入到单车辆的物料配送模型中,运用Cplex软件进行求解,确定每辆车所要配送的次数、每次配送的工位次序和配送的时间。
例如有10个工位需要物料配送,由车辆A和B为其服务,每辆车的容量是10,具体配送信息如图1所示。染色体编码表示工位2、5、3、7、4、6 由车辆 A 服务,车辆A需要往返两次,第一次配送工位2、5、3,配送的次序是2→5→3,第二次配送7、4、6,配送的次序是7→4→6;车辆B只需要配送一次,配送的工位次序是 8→1→9→10。

图1 配送信息Fig.1 Delivery information
2.2.2 评价的目标函数
本文选取总的配送时间作为目标函数值,该目标函数值包括车辆的行驶时间和物料的装卸时间。总的配送时间越短,染色体的适应度越好,染色体对应的解越优。每个染色体对应的总的配送时间就是所有车辆中配送完成时间的最大值。
本文采用轮盘赌策略选择染色进行交叉和变异。假设种群的规模是psize,具体的选择过程如下。
①计算种群的总的适应度函数值F,其表达式为:

式中:eval(Xh)为第Xh个染色体的适应度函数值,即配送的总时间。
②计算每个染色体Xh被选择的概率Ph,其表达式为:
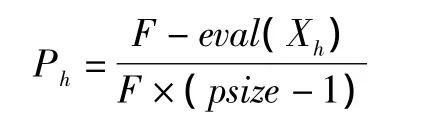
式中:h=1,2,…,psize。
③ 计算每个染色体Xh的累积概率密度
④ 生成一个随机数r∈(0,1]。
⑤ 如果qh-1<r≤qh,则选取染色体Xh进行遗传操作。
2.2.3 交叉和变异
本文采用顺序交叉法,两个父代进行交叉产生两个子代,保证种群规模的不发生变化。具体的交叉过程如图2所示。
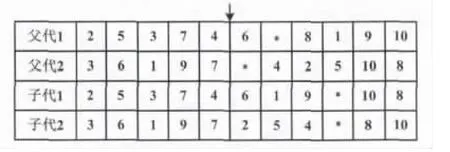
图2 交叉机制Fig.2 Crossover mechanism
变异操作能够扩大解的搜索空间,增强解的多样性,避免解过早陷入局部最优。本文采用反转变异,具体实施过程如图3所示。

图3 变异机制Fig.3 Mutation mechanism
2.3 三阶段启发式算法
本文设计的启发式算法分3个阶段,每个阶段建立了相应的数学模型,运用Cplex软件对模型进行求解。
①第一阶段
根据工位的需求信息和车辆的容量,计算出车次的分配方案。此阶段的目标函数是最小化车次数,给出每个车次配送的具体工位,将此配送方案作为第二阶段输入,数学模型如下。

式中:qi为工位的物料需求;i=1,2,…,n;Q为车辆的容量限制。
式(12)表示从仓库派出的车次数最少;式(13)表示每个工位需要一个车次为其提供物料;式(14)表示每个车次配送的物料数量不能超过车辆的容量限制。
②第二阶段
对第一阶段车次的分配方案进行优化,优化的目标是使每个车次的行驶时间最短,求出每个车次对所服务的工位进行配送的先后次序;并将此车次的行驶时间和装卸货时间进行合并,求出此车次的配送完成时间作为第三阶段的输入。
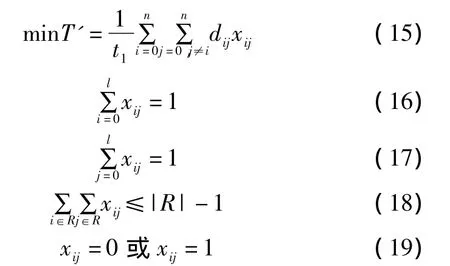
式中:i=0,1,…,l;j=0,1,…,l;R⊆{1,2,…,l}。
式(15)表示目标函数求车次的行驶时间最短;式(16)和式(17)表示每个工位只需要一个车次为其服务;式(18)表示消除支路;式(19)表示决策变量的取值。
③第三阶段
对车次进行合并,用有限的车辆完成所有车次的配送,要求车辆中最大的配送时间最小。设R={R1,R2,…,Rm},表示 m 个车次的集合;K={K1,K2,…,Kk}表示k(k≥2)辆车的车辆集合;车次Ri的配送完成时间为 Ti(i=1,2,…,m)。Ci(i=1,2,…,k)表示第i辆车的配送完成时间,表示总的配送完成时间,表示最优方案的总的配送完成时间。

式中:i=1,2,…,m;j=1,2,…,k。
式(20)表示目标函数,要求总的配送完成时间最短;式(21)表示每个车次只需一辆车完成配送;式(22)表示每辆车配送完成时间;式(23)表示决策变量。
3 算例分析
现有一条生产线由15个工位组成,工位和仓库的信息如表1所示。仓库中有3辆相同的车辆为这些工位进行配送物料,车辆的最大容量是18,行驶速度是0.75 m/s,每单位物料的装卸货时间是60 s。

表1 工位和仓库的信息Tab.1 Information of work positions and inventories
3.1 遗传算法求解
设遗传算法求解的参数为:psize=30,MAXGEN=100,PXOVER=0.8,PMUTATION=0.1。采用 Visual C#编程实现,计算机共需要运行296 s,计算结果如表2所示。车辆1需要完成两个车次的配送,需要的配送时间是3 004 s;车辆2需要完成3个车次的配送,需要的配送时间是2 880 s;车辆3需要完成两个车次的配送,需要的配送时间是2 916 s;完成所有工位的物料的配送取3辆车的最大值3 004 s。

表2 遗传算法计算结果Tab.2 Calculation result of genetic algorithm
3.2 三阶段启发式方法求解
采用三阶段启发式方法在Cplex平台上对此算例进行求解,计算机共需要运行28 s。第一阶段计算得到完成配送至少需要6个车次;第二阶段计算得到每个车次的最小的配送时间及每个车次的配送工位的次序;第三个阶段对车次进行了合并,每辆车需要完成两个车次的配送,车辆完成所有的物料配送所需要的最短配送时间是3 083 s。三阶段的计算结果如表3所示。

表3 启发式方法的计算结果Tab.3 Calculation result of heuristic method
3.3 两种方法的比较
从以上计算可以看出,改进的遗传算法得到的目标函数值是3 004 s,而三阶段启发式算法得到的目标函数值是3 083 s,改进的遗传算法要优于三阶段启发式算法;且三阶段启发式算法的计算速度优于改进的算法。
4 结束语
通过上述算例的计算,证明了算法能够有效地解决生产线中物料的配送问题,提高物料配送的效率,防止生产线因为物料供应不及时而停顿,有效保证了流水线的连续性生产。
[1] Dantzig G B,Ramser J H.The truck dispatching problem[J].Management Science,1959(6):80 -91.
[2] Ghoseiri K,Ghannadpour S F.Multi-objective vehicle routing problem with time windows using goal programming and genetic algorithm[J].Applied Soft Computing,2010,10(4):1096 -1107.
[3] Donati A V,Roberto M,Norman C,et al.Time dependent vehicle routing problem with a multi ant colony system[J].European Journal of Operational Research,2008,185(3):1174 -1191.
[4] Anbuudayasankar S,Ganesh K,Lenny K S C,et al.Modified savings heuristics and genetic algorithm for bi-objective vehicle routing problem with forced backhauls[J].Expert Systems with Applications,2012,39(3):2296-2305.
[5] Qureshi A G,Taniguchi E,Yamada T.Exact solution for the vehicle routing problem with semi soft time windows and its application[J].Procedia-Social and Behavioral,2010,2(3):5931 -5943.
[6] Müller J.Approximative solutions to the bicriterion Vehicle routing problem with time windows[J].European Journal of Operational Research,2010,202(1):223 -231.
[7] 祁文祥,陆志强,孙小明.带软时间窗的集货与送货多车辆路径问题节约算法[J].交通运输工程学报,2010,10(4):99 -103.
[8] Boysen N,Bock S.Scheduling just-in-time part supply for mixedmodel assembly lines Original Research[J].European Journal of Operational Research,2011,211(1):15 -25.
[9] 蒋丽,丁斌,臧晓宁.以工位为中心的生产物流配送优化[J].计算机集成制造系统,2009,15(11):2154 -2159.
[10] 曹振新,朱云龙.混流轿车总装配线上物料配送的研究与实践[J].计算机集成制成造系统,2006,12(2):285-291.

