考虑城市堵车信息的出租车调度系统

姚仲敏，龙昭鹏，李 强

(齐齐哈尔大学通信与电子工程学院，黑龙江齐齐哈尔161006)

1 引 言

目前出租车调度系统主要是在调度中心接收到乘客的调度请求后，选择最合适的出租车为乘客提供乘车服务.一定程度上缓解了乘客“打车难”、“人找车，车找人”的现象，也一定程度上降低了出租车的空载率［1-4］.但是没有考虑实时的城市道路交通状态，使得原本最合理的调度(路程最短)，因为调度的出租车可能需要经过堵车区域，不能及时为乘客提供服务，甚至进一步加重了该区域的道路拥堵.随着城市车辆的不断增加，堵车成为现今交通重大难题［5］.考虑城市道路堵车状况的出租车调度系统，具有重要的意义和价值.

2 系统结构

系统主要包括三部分:GPS手机、GPS出租车和调度中心.GPS手机用于定位乘客当前位置经纬度信息，向调度中心发送调度出租车请求.GPS出租车向调度中心发送堵车信息和节点更新信息.调度中心用于接收乘客的调度请求信息和出租车发送的信息，并调度最佳出租车为乘客提供乘车服务.系统结构如图1所示.

图1 系统结构Fig.1 System structure

3 系统节点

出租车的调度需要知道乘客所在位置，空载出租车位置以及城市道路分布.本系统是根据乘客所在位置，向周围扩展寻找空载出租车.所以，源节点为乘客所属的城市道路节点，城市道路节点代表城市交叉路口，目的节点需要调度之后才能确定.各城市道路节点的分布、连通性和直接距离即可反映城市道路分布情况.

3.1 城市道路节点

本系统中，城市道路节点为固定节点，节点属性如表1所示.

表1 节点属性Table 1 Node attributes

NodeGPS:城市道路节点经纬度信息，表示节点所在交叉路口的具体位置.

neighborNode:邻居节点，记录了本节点和各邻居节点的位置关系和距离.

nodeList:一个排序的链表，记录了到最大调度范围内各节点的最短距离，及经过节点的数量.

hasTaxi(n):有出租车信息，表示附近正开往该节点的空载出租车数量.

tJamCounter(c):堵车计数器，用来描述该节点的堵车状态.

Weight(w):权重，值在0-1之间.表示该节点在城市交通中的重要性.越繁华的街道节点，其权重值越大.

Loss(l):出租车经过该城市道路节点时的损耗.

3.2 源节点和目的节点

本系统中，源节点即乘客所在城市道路节点.用适当的矩形代表某城市，矩形左上角经纬度为［x1，y1］，右下角经纬度为［x2，y2］.本系统的网格大小为［ptl×(x2-x1)，ptl×(y2-y1)］，其中ptl表示该城市的交叉路口密度.系统依据乘客所在位置，快速定位乘客所在网格，并确定一个距离乘客最近的城市道路节点作为源节点.

当出租车经过一个交叉路口(城市道路节点)时，根据GPS数据和城市道路节点属性，分析出正在开往和离开的城市道路节点，发送这两个城市道路节点的hasTaxi属性更新信息至调度中心.

3.3 堵车信息

正常通车时，车辆即使因路口红灯不能及时通过交叉路口，在连续两个红灯期间也会有一段行驶距离.所以，当出租车引擎开启，在一段时间tg(tg大于红灯时间)内出租车车速始终低于城市最低行车速度且行驶距离小于固定距离(如40 m)时，才向调度中心发送道路堵车信息，以防止出租车位于交叉口停车(停车时间不长，一般小于tg)和正常通车造成的误报.调度中心接收到堵车信息，堵车计数器值c增加，c主要是靠出租车数量和堵车时间的积累，即使偶尔出现一两辆出租车误报的情况对系统的影响很小，c的计算方法如下:

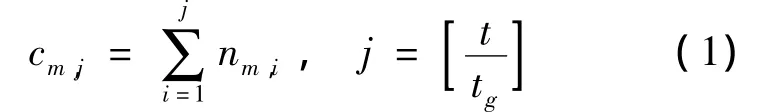
式中 cm，j表示在j时间段内m节点的堵车计数器值;nm，i表示i时间段内被堵于m节点的出租车数量;t表示堵车时间;tg表示更新堵车信息的时间间隔.当堵车计数器值c不为0时，出租车经过节点所在区域会有额外损耗，额外损耗计算方法如下:

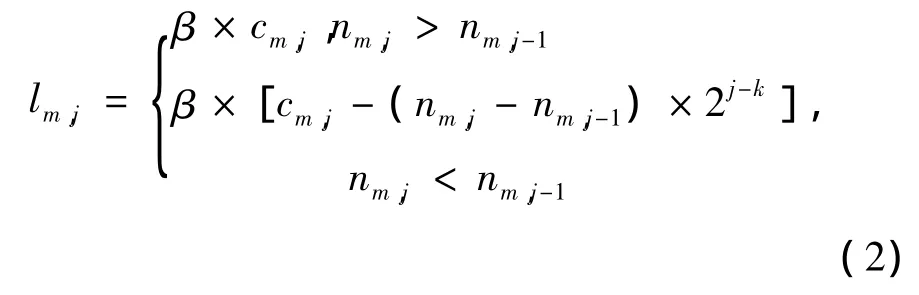
式中 lm，j表示在j时间段内经过m节点的额外损耗(m)，为非负数，lm，j＜ 0时，计为0;β 表示单位额外损耗(一个堵车计数器值所带来的额外损耗)，k表示该区域堵车情况开始出现缓和的时刻，此时堵车数量开始减少.出租车经过城市道路节点m时的损耗的计算方法如下:

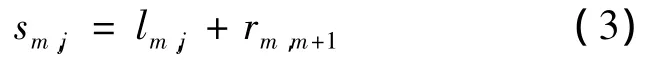
式中 sm，j表示出租车在j时间段内经过节点m的损耗(m)，rm，m+1为城市道路节点m到其下一节点(m+1)的距离.而出租车与乘客之间的路程为出租车经过的各节点的损耗之和，即

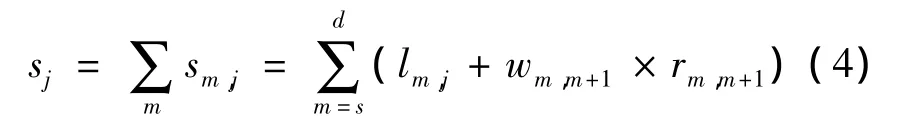
式中 sj表示j时段内的乘客与出租车之间的路程(m)，s表示乘客所属节点;d表示出租车所属节点;wm，m+1表示城市道路节点m到其下一节点(m+1)所在道路的权重.

4 调度算法

本系统采用Dijkstra算法结合堵车信息进程出租车调度.Dijkstra算法是求最短路径的经典算法，采用Dijkstra算法调度出租车，确定乘客到调度范围内各空载出租车的最短距离，从中选择距离最短的出租车作为调度对象.

Dijkstra算法的基本思路是:每次新扩展一个距离最短的点，更新与其相邻的点的距离.当所有边权都为正时，由于不会存在一个距离更短的没扩展过的点，所以这个点的距离永远不会再被改变，因而保证了算法的正确性.假设每个点都有一对标号(dn，pn)，其中dn为m到n的最短路径;pn为m到n的最短路径中n的前一节点.求解m到终点n的最短路径的步骤如下［6］:

Step 1 初始化.设起点m的标号dn=0，pn为空.其他所有节点的标号设为dn= ，pn为空.标记起始点m，记k=m，其他所有节点为未标记节点.

Step 2 检验从所有已标记的点k到与其直接连接的未标记的点n的距离，设dn=min{dn，dn+lkn}，式中lkn为点k到与其直接连接点n的距离.

Step 3 从所有dn中选取最小的点i，di=min{dn，所有未标记的点n}.则点i被选为最短路径中的一点，并设定为已标记.

Step 4 考察所有点，如果都已经标记，则退出算法，否则记k=i，返回Step 2.

Dijkstra算法中每一个节点需要计算到其它所有节点的距离，搜索具有盲目性，算法时间复杂度较高为O(n2)，其与城市道路节点数n成指数增长，所以减少搜索节点数量是降低算法时间复杂度的重要方法，目前研究的热点是通过限制搜索区域，如方向夹角［7］、直线加速法［8］、矩形区域算法［9］等.这些算法在导航(即知道目的节点情况下的搜索)中性能突出.而本系统中目的节点(空载出租车)在发起调度时不确定，上述算法不适用.为减少搜索节点数，本文提出在最大调度范围内进行出租车调度，从出租车司机的经济利益考虑，司机不会接受距离太远的调度请求，而且，这种过远距离的调度会浪费能源，调度失去意义.

本系统发起调度时，以乘客所属节点S为源节点，将S周围处于调度范围(r)内的所有节点加入集合H，同时将有空载出租车的节点加入集合D.只需在集合H中采用Dijkstra算法计算到集合D中所有节点的距离.其时间复杂度为O［card(H)×card(D)］，其 中 card(D)＜ card(H)＜ ＜ n，card(D)、card(H)分别表示集合D和集合H中元素个数.此方案很大程度上降低了原Dijkstra算法的时间复杂度.系统具体调度步骤如下:

Step 1 H=∅;

Step 2 确定乘客所属城市道路节点(S)，H:={S}，将S作为指定元素;

Step 3 依次查看指定元素的各邻居节点，根据式(4)计算S到邻居节点的路程(s)，若s＜r，H:={指定元素邻居节点}，若指定元素邻居节点的hasTaxi属性值(v)大于零，D:={指定元素邻居节点};

Step 4 若非集合H中的最后一个元素，则将下一个元素作为指定元素，返回Step 3;

Step 5 根据集合H中的元素，采用Dijkstra算法计算S到集合D中各元素的最短距离;

Step 6 将得到的最短距离排序后放入到节点的nodeList属性表中;

Step 7 按nodeList表依次调度出租车，有出租车司机同意则结束调度，否则调度失败.

5 实验结果

以齐齐哈尔市区龙沙区内部分主干道为基础进行仿真，由于都是主干道，权重w都为1，且该选定区域内共有21个节点，在Visual C++6.0中采用邻接表实现Dijkstra算法，采用21×21的二维数组表示选定区域内各城市道路节点之间的距离.邻接矩阵如图2所示.

图2 邻接矩阵图Fig.2 Adjacency matrix

实验仿真时，堵车情况和堵车节点随机出现，在一次具体的仿真中，节点3出现堵车，具体的堵车情况和经过节点3的额外损耗如图3所示.图3中给出了堵车数量n和β分别为10，30，50时额外损耗(l)的变化曲线，其中，所堵出租车数量n的变化情况为

节点3处堵车时系统调度结果如表2所示.表2中，S为乘客所在节点，D为出租车所在节点;J为堵车节点;t表示堵车时间;s为调度需要行驶的路程;P为调度出租车行驶的路径.由表2知，从节点6调度出租车至节点17，当β分别为10、30、50时，系统分别在节点3发生堵车的第6、4、3 min后改变调度路径，所改变的调度路径中不再包含节点3，从而规避堵车区域，在第13 min(正常通车)恢复正常调度.而从节点6调度出租车至节点11，当β为10时，调度结果始终保持不变，没有改变调度路径.经查，节点11地处较为偏僻地带，交通道路少，改变路径消耗很大.但是，当 β分别为30、50时，系统分别在第5、4 min后可以改变调度路径，规避堵车区域，在第13 min(正常通车)恢复为正常调度.可见系统调度直接受β的影响，不同的β值对堵车的灵敏度不同，设置合适的β值能提高系统规避堵车区域的成功率，如表2中β=20的调度结果比较理想.而未考虑城市道路堵车情况的出租车调度系统(即，目前的调度系统)，其调度结果与没有发生堵车的调度结果一样，并保持不变，不能规避堵车区域.

图3 β为10，30，50时l的变化曲线图Fig.3 Curves of l when β is 10，30，50

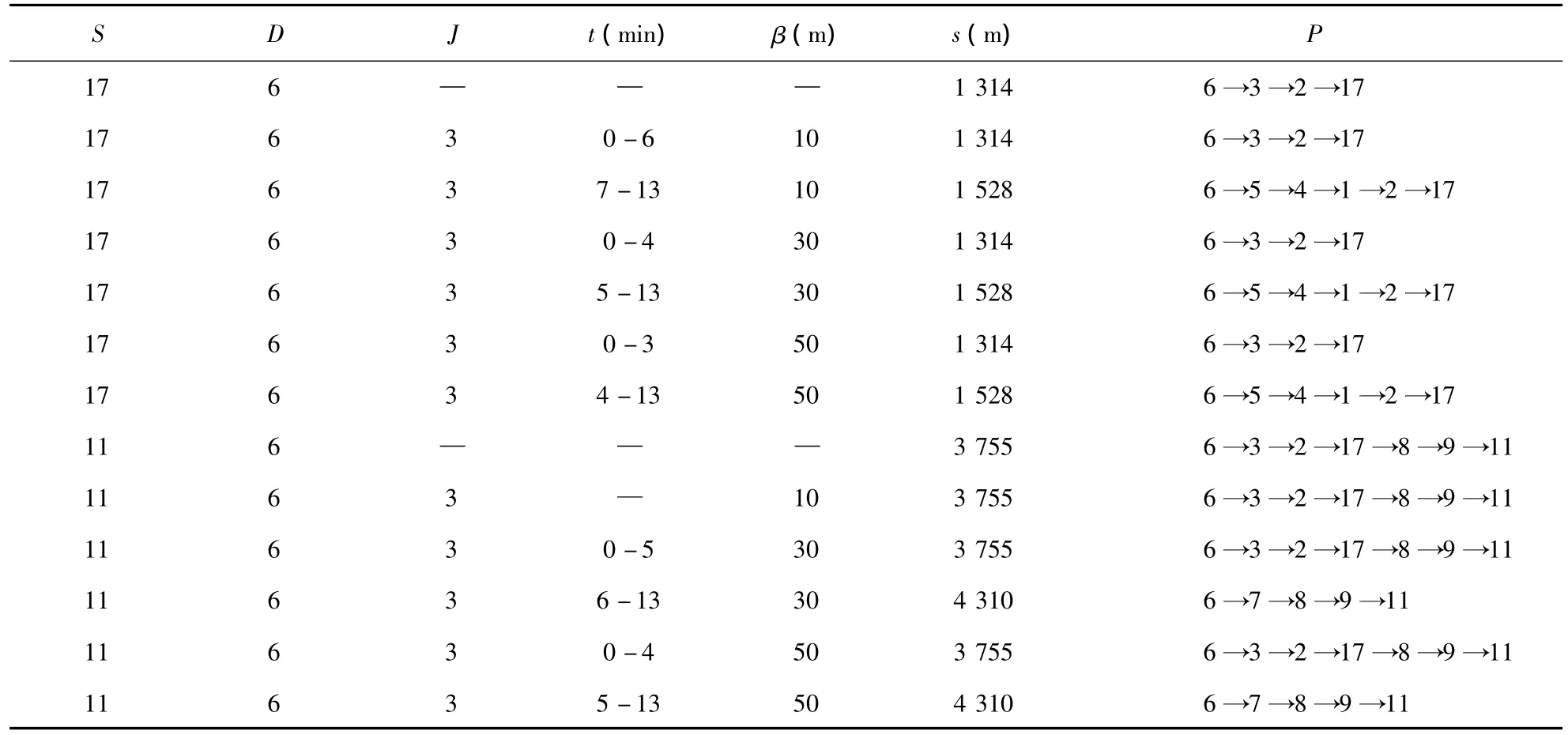
表2 调度结果Table 2 Scheduling results

6 研究结论

在城市堵车越来越严重的情况下，目前的出租车调度系统没有考虑城市堵车状况，调度的出租车可能需要经过堵车区域，不能及时解决乘客需求.本文提出了一种考虑城市堵车信息的出租车调度系统，当发生堵车时，通过增加车辆经过该区域损耗的方法，实现出租车避开堵车区域.不同的β值，对应系统对堵车的不同灵敏度，通过实验仿真，设置合理的β值，系统可根据堵车情况的严重程度，合理规划调度出租车的行驶路径，避开城市堵车较严重区域.

［1］俞斌，朱海清，黎美丽.基于GPS/GIS/GSM的出租车调度系统［J］. 城市公共交通，2010，4:41-44.［YU B，ZHU H Q，LI M I.Taxi dispatch system based on GPS/GIS/GSM［J］.Urban Public Transport，2010，4:41-44.］

［2］周先春，石兰芳，周杰.一种出租车调度中心系统的设计［J］. 电子技术应用，2012，38:136-138.［ZHOU X C，SHI L F，ZHOU J.A design of taxi dispatch center system［J］.Application of Electronic Technique，2012，38:136-138.］

［3］周晓敏，赵红玉，俞建新.基于GPS的出租车呼叫与调度系统［J］.计算机工程与设计，2009，30(21):4995-4997.［ZHOU X M，ZHAO H Y，YU J X.Taxi calling and scheduling system based on GPS［J］.Computer Engineering and Design，2009，30(21):4995-4997.］

［4］杨宏业，张跃.一种新的GPS出租车调度系统的设计与实现［J］.电子技术应用，2002(6):44-46.［YANG H Y，ZHANG Y.Design and implementation of a new GPS taxi dispatch system［J］.Application of Electronic Technique，2002(6):44-46.］

［5］魏卓新.城市道路何时不再拥堵［J］.江淮，2012(7):47-48.［WEI Z X.When the city road is not jam traffic ［J］.Jiang Huai，2012(7):47-48.］

［6］冯欣欣.Dijkstra算法在嵌入式GIS中的优化实现［J］. 北京理工大学学报，2009，29(10):873-876.［FENG X X. Efficient implementation ofdijkstra algorithm in embedded GIS［J］.Transactions of Beijing Institute of Technology，2009，29(10):873-876.］

［7］董俊，黄传河.改进Dijkstra算法在GIS导航应用中最短路径搜索研究［J］.计算机科学，2012，39(10):245-247.［DONG J，HUANG C H.Research on shortest path search of improved dijkstra algorithm in GIS navigation application［J］.Computer Science，2012，39(10):245-247.］

［8］倪怡，邱成龙，杨皓然.面向行车诱导的最优路径算法研究［J］.自动化与仪器仪表，2012(3):145-149.［NI Y，QIU C L，YANG H R.The study of the optimal path algorithm for driving induction［J］.Automation ＆Instrumentation，2012(3):145-149.］

［9］周影，曹菡，李军霞.一种限制区域的最短路径查找算法［J］.微电子学与计算机.2007，24(8):110-112.［ZHOU Y，CAO H，LI J X.A Shortest route-planning algorithm within a restricted area［J］.Microelectronics＆ Computer，2007，24(8):110-112.］