经编网眼织物工艺参数对力学性能的影响*

肖伟发 张 磊 蒋金华，3 陈南梁，3

(1.上海经纬〔集团〕有限公司，上海，200021;2.东华大学纺织学院，上海，201620;3.东华大学产业用纺织品教育部工程研究中心，上海，201620)

随着经济及技术的发展，经编产品在产业方面的优势越来越被人们所重视，经编网眼织物便是其中之一。经编网眼织物具有网眼大小可控、无结头、表面光滑、耐磨损、质轻、形状稳定等优点［1］，目前被广泛用作建筑、运输及娱乐设施的防护网［2］，农业用捆扎网、遮荫网［3］、防风网以及渔业用渔网［4-7］等，甚至在航天航空领域，网眼织物也得到了很好的应用［8］。近年来，随着产业用网需求的增加，网眼织物的力学性能受到越来越多的关注［9］。本文从经编拉舍尔网眼织物编织过程中的牵拉密度和送经量两个工艺参数方面，对网眼织物的力学性能加以探讨。

1 材料及试验

1.1 试样材料

本文采用一种两梳栉一穿一空的四列开口经缎编织的菱形网眼织物为试样，其线圈结构［10］见图1。原料为江苏恒力化纤股份有限公司提供的75D/36f的涤纶低弹丝，在E16的拉舍尔经编机上通过改变不同的牵拉密度和送经量织出不同网眼大小的5块织物。这5块织物的编号和结构参数如表1所示。

图1 经编网眼织物线圈结构

1.2 试验仪器及方法

本文主要对由不同工艺参数织制的经编网眼织物进行纵向和横向拉伸试验。目前，我国还没有相关的经编网眼织物的测试标准，因此，为了取得相对规范的测试结果，现参照GB/T 4925—1985《合成纤维渔网片断裂强力与断裂伸长率试验方法》。测试仪器为上海华龙测试仪器有限公司WDW-20型微机控制电液伺服万能实验机，其最大载荷为20 kN，最大量程为1 200 mm，拉伸速度为0.5～500 mm/min，试样在夹具间的有效长度为100 mm，宽度为10目(见图2)。试验时，将网片试样平整地夹入上夹具，并使目脚互相靠紧，夹入下夹具内，然后进行试验，测得断裂强力与断裂伸长。

表1 不同密度经编网眼织物编号和结构参数

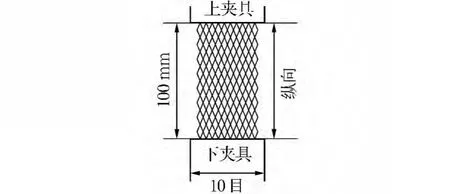
图2 单向拉伸示意图

1.3 试验结果

将 A、B、C、D、E 5 块试样自由松弛3 d，然后分别对它们进行纵向和横向的拉伸试验。所得测试数据如表2所示。

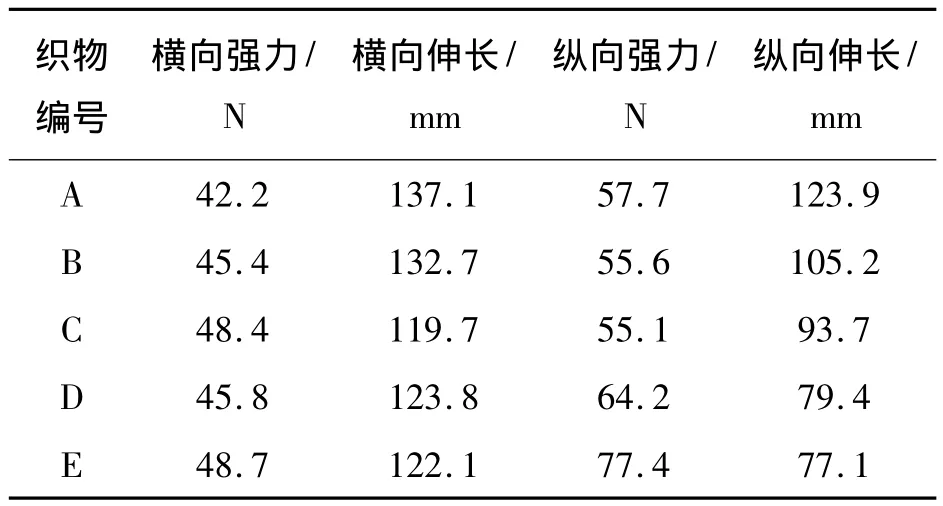
表2 不同织物的拉伸测试结果

2 结果与讨论

2.1 牵拉密度对网眼织物力学性能的影响

2.1.1 牵拉密度与断裂强力的关系

图3为牵拉密度与网眼织物纵、横向强力之间的关系。从图3中可以看出，纵向强力始终比横向强力大，而且它们两者与牵拉密度都呈二次函数的关系，只是牵拉密度与纵向强力的关系曲线为一凹曲线，而牵拉密度与横向强力的关系曲线为一凸曲线。因此，必然存在一种牵拉密度使得网眼织物的纵向和横向强力的差距最小，使织物的各向同性性能得到改善。经过分析计算，得到两条曲线的拟合方程。

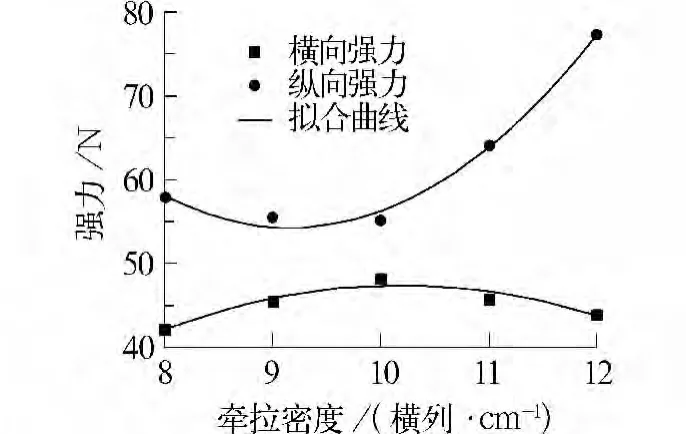
图3 牵拉密度与网眼织物纵、横向强力之间的关系

牵拉密度与网眼织物纵向强力的关系方程:

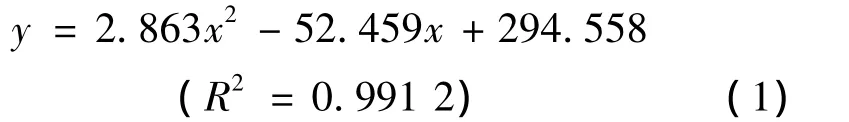
牵拉密度与网眼织物横向强力的关系方程:

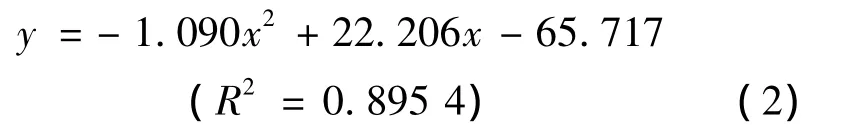
2.1.2 牵拉密度与断裂伸长的关系

图4为牵拉密度与网眼织物纵、横向断裂伸长之间的关系曲线。由图4可知，织物的纵、横向伸长与牵拉密度成一次函数的关系，并且随着牵拉密度的增大，断裂伸长减小。这主要是因为牵拉密度增加，织物线圈长度减小，网孔变小，织物受拉伸后，线圈转移长度也变小，从而使得织物的拉伸断裂伸长减小。此外，织物的横向伸长始终大于纵向伸长，而且随着牵拉密度的增加，它们两者之间的差距会越来越大。

2.2 送经量对网眼织物力学性能的影响

2.2.1 送经量与断裂强力的关系

图5为送经量与网眼织物纵、横向断裂强力之间的关系曲线。由图5可知，送经量与网眼织物纵、横向强力之间的关系同牵拉密度与纵、横向强力之间的关系类似。它们的关系曲线都是二次函数曲线，而且也存在某一种送经量能使网眼织物的各向同性性能提高。只是两种拟合曲线的方程式存在差异。经过分析计算，得到两条曲线的拟合方程。

图4 牵拉密度与网眼织物纵、横向伸长的关系

图5 送经量与网眼织物纵、横向强力的关系

送经量与网眼织物纵向强力的关系方程:

送经量与网眼织物横向强力的关系方程:

2.2.2 送经量与断裂伸长的关系

图6为送经量与网眼织物纵、横向断裂伸长之间的关系曲线。由图6可知，织物的纵、横向伸长与送经量成一次函数的关系，并且随着送经量的增大，断裂伸长逐渐增大。这是因为送经量增加，织物每个线圈的长度也随之增大，织物受拉伸时，线圈的圈弧和圈柱之间的转移长度也增大，从而使得织物的拉伸断裂伸长变大。

2.3 经编网眼织物的力学各向同性的优化工艺

通过对不同牵拉密度和送经量与网眼织物纵、横向力学性能的探讨，得出了它们之间关系的拟合方程。从这些方程出发，经过计算和实际的比较发现，当牵拉密度为9.4横列/cm，送经量为2 722 mm/480横列时，所织出的网眼织物的纵、横向力学性能的差异最小，极大地提高了经编网眼织物的各向同性性能。

图6 送经量与网眼织物纵、横向伸长的关系

3 结语

(1)通过试验发现，经编网眼织物的纵向强力始终比横向强力大，而且它们两者与牵拉密度都呈二次函数的关系。织物的纵、横向伸长与牵拉密度则成一次函数的关系，并且随着牵拉密度的增大，断裂伸长减小。

(2)送经量与网眼织物纵、横向强力之间的关系也是二次函数曲线。织物的纵、横向伸长与送经量也呈一次函数的关系，随着牵拉密度的增大，断裂伸长逐渐增大。

(3)经过优化计算得出，牵拉密度为9.4横列/cm，送经量为2 722 mm/480横列时，网眼织物的纵、横向力学性能的差异最小，经编网眼织物的各向同性也最好。

［1］蒋高明.现代经编工艺与设备［M］.北京:中国纺织出版社，2001.

［2］邱红娟，徐燕娜.经编防护网的产品开发及性能探讨［J］.针织工业，2005(9):1-3.

［3］夏风林，梅德山.经编农用遮荫网遮光率测定与分析［J］.产业用纺织品，2003，21(12):26-28.

［4］ANDERSON T W，CARR M H.BINCKE:A highly efficient net for collecting reef fishes［J］.Environmental Biology of Fishes，1998，51(1):1

［5］BARTHEL B L，COOKE S J，SUSKI C D，et al.Effects of landing net mesh type on injury and mortality in a freshwater recreational fishery［J］.Fisheries Research，2003，63(2):275-282.

［6］石建高，王鲁民，汤振明，等.超高分子量聚乙烯和锦纶经编网片的拉伸力学性能比较［J］.中国水产科学，2004，11(Z1):40-44.

［7］石建高，王鲁民，徐君卓.高强度聚乙烯菱形网目经编网片的力学性能初步研究［J］.中国海洋大学学报:自然科学版，2006，36(3):410-414.

［8］蒯斌.用于可调伞形天线的网眼织物的发展［J］.国外纺织技术:针织服装分册，1992(2):33-35.

［9］刘晓明，陈南梁，冯勋伟.经编网格织物工艺参数对强力的影响［J］.针织工业，2007(6):20-22.

［10］龙海如.针织学［M］.北京:中国纺织出版社，2008.