非线性聚集生长理论的研究及其应用

梁坚生，陈 乐

（玉林师范学院，广西 玉林 537000）

非线性聚集生长是一种常见的不可逆自然现象，如大气颗粒物的形成过程、固体沉积物的凝聚、液体悬浊物的沉淀、点阴极下金属的电沉积、准晶体的生长等过程，该类过程的一个显著特点就是生长得到的凝聚物（聚集物）大多具有分形结构[1－5]，如图1所示。为了研究非线性聚集生长过程的物理机制及其相关的物理特性，1981年美国物理学家Witten和Sander就提出了著名的扩散限制凝聚模型（Diffusion－limited aggregation，简称DLA模型 ），该模拟最初用于研究悬浮在溶液或大气中的煤灰烟尘和粉末等微粒对凝聚过程。DLA模型及在DLA基础上发展的多种模型（如1983年由物理学家P.Meakin在DLA模型基础上提出的集团—集团凝聚模型，简称CCA模型）均已成为研究非线性聚集生长的重要模型[6－7]。

图1 从实验获得的烟雾颗粒物的放大图像

由于DLA模型相对简易，且模拟得到的凝聚物与实验得到的电化学沉积物在形态、结构上又非常相似，所以在过去的30多年里面，人们利用DLA模型及其相关模型模拟研究了自然界中大量聚集过程，探索了凝聚物形成的物理机制、过程特点及影响凝聚的各种因素。实验研究方面，由于电化学沉积物与DLA模型模拟得到的凝聚物在形态上较为相似，人们便将电沉积过程的研究与DLA模拟的研究密切地联系起来。长期以来，人们利用计算机模拟与实验研究相结合的方法对非线性聚集生长的理论进行了大量的研究并取得了丰富的成果。另外，非线性聚集生长的理论研究成果还在实际凝聚生长研究方面有着广泛的应用。例如，非线性聚集生长的计算机模拟能较好地模拟自然中大气颗粒物的形成过程，这有利于研究固体沉积物的物理性质和沉积的生长过程。其最大的优点就是可以通过计算机的方法，轻易地实现非线性聚集生长过程的模拟，通过改变模拟的参数探索不同条件下凝聚物的生长，以及不同条件下形成凝聚物的结构特征，分析形成的物理机制以及凝聚物的分形维数等方面的信息。非线性聚集生长理论还在薄膜生长方面有着广泛的应用，对于探索不同条件下薄膜的生长，以及形成薄膜的特性等方面，具有良好的应用前景。

本文将介绍非线性聚集生长计算机模型与生长规则和非线性聚集生长的实验原理与装置，阐述了计算凝聚物分形维数的模拟方法和实验计算方法，以及非线性聚集生长理论在大气颗粒物、薄膜生长方面的应用研究，这对于全面了解非线性生长理论及其应用有一定帮助。

1 二维DLA模型的计算机模拟与生长规则

P.Meakin最先在文献[8]中给出了二维传统DLA模型的计算机模拟与生长规则，其基本思想如下：

（1）将二维正方形平面分割成许多相同小方格，形成点阵，在点阵的正中心放置一个粒子，称为种粒子。

（2）在以种粒子为圆心，半径足够大的圆周上随机释放一个粒子，并在点阵内作无规行走，步距为一个小方格的边长。如果粒子抵达种粒子（或凝聚集团其它粒子）的最近邻（或次近邻）格点，则停止运动并固定成为集团的一个组成部分。

（3）如果粒子行走到与种粒子距离过远时，取消该粒子。重复（2）过程。

（4）不断重复（2）和（3）过程，则可形成逐渐长大的DLA凝聚集团。

模型如图2所示，由该模型所得到的一个粒子数凝聚物如图3所示，凝聚物具有统计自相似性的分形特征和开放性的树枝状结构。

图2 DLA模型的计算机模拟图

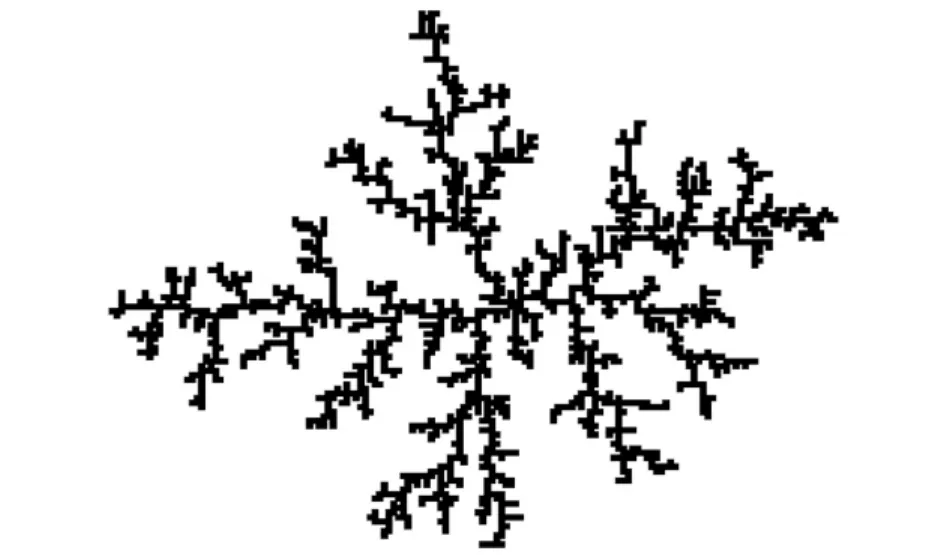
图3 随机模拟得到粒子数的凝聚物

2 非线性聚集生长的实验原理与装置

通过在硫酸锌、硫酸铜溶液中极进行电解沉积的方法，可以得到在形态、结构上与二维DLA模拟凝聚物相似的沉积物，该类沉积物还具有DLA凝聚物相似的分形特征。通过控制或者选取不同的溶液浓度、不同的电场强度和不同的电极形状等，可以得到不同形状和结构的沉积物。

在文献[9]中，实验将ZnSO4溶于蒸馏水中配成0.5mol／L的 水溶液。实验装置如图4所示，环绕培养器（直径约为6cm）边缘的细铜薄片作为阳极，培养器中心区域上方悬挂的细铅笔心作为点阴极，实验中以滤纸作为载体进行，如图5所示。通过该实验，选取合适的电压，即可以很快得到Zn的电沉积物。从沉积物的形态来看，沉积物与模拟凝聚物非常相似，具有开叉性的树状结构。

图4 电沉积Zn实验装置图

在传统的DLA模型中，随机扩散是粒子凝聚过程中起主导作用的生长动力，利用扩散理论对凝聚物生长形成的物理机制进行了深入研究，并在随机扩散理论的框架内对随机生长进行了大量的计算机模拟，取得了丰富的理论成果，且大大加深了对非线性聚集生长形成机制的认识。然而，相对于电解沉积生长的实验而言，仅靠扩散动力并不能有效地形成沉积生长，必须在溶液内部通以电流，以便形成合理的电场分布，电场力在沉积物的形成过程中发挥了至关重要的作用。正是由于电场力的作用，使得沉积物的生长过程及沉积物的形状与电场线的分布有关，所以电解沉积物的形状与电极的形状有关，不同的阴极形状将会得到不同形状的沉积物[9]，如图6和7所示。

图5 点形阴极沉积物生长花样

图6 线形阴极沉积物生长花样

图7 圆形阴极沉积物生长花样

3 凝聚物分形维数的计算

分形结构是非线性聚集生长凝聚物的一个重要特征，通过分形维数可以定性地描述凝聚物的分形特征。自从DLA模型问世以来，人们曾做了大量的工作来确定凝聚集团的分形维数。其中，在计算机模拟上较为常用的方法是“密度相关函数法”[6]和“回转半径法”[8]等，在理论上较为常用的则是物理学家M.Muthukumar利用“平均场理论”（Mean－Field Theory）导出的计算DLA集团分形维数的方法[10]。虽然方法各异，但它们得到的结果却基本一致，都认为较为理想的计算了DLA集团的分形维数。

对于回转半径法，一般令DLA凝聚集团的回转半径为[8]：

其中：N为凝聚集团的粒子数，ri为第i个粒子离种粒子的距离。则Rg与N的标度关系为：

式中Df为凝聚集团分形维数。由上式，如果以lnRg为横坐标，lnN为纵坐标，作出Rg与N的双对数曲线lnRg～lnN，则Df为该曲线的斜率。通过计算机模拟容易得到[11]，二维DLA凝聚集团，其维数Df≈5／3，三维DLA凝聚集团，Df≈2.50。

对于实验得到沉积物，由于实验难以实现对沉积物“回转半径”的计算，所以对于实验沉积物分形维数的计算，一般利用电镜拍下沉积物的生长图并导入计算机，然后通过编写计算机程序对沉积物的分形维数进行计算。目前该方法大多采用“盒维数”的思想计算其分形维数，该方法的基本思想如下：

（1）将沉积物的图像导入计算机程序中，然后对图像进行二值化处理，即使图像上每一个像素点为黑或白两种颜色，如图6所示。

（2）采用二维的正方形网格对图形进行覆盖，然后把二值化图像转化成数据文件，其行列数分别对应于二值图的行列数，每一个数据取值1或0，如果是黑色，则对应的数据取1，否则取0。

（3）在正方形网格的中心选择一点，并以该点为圆心作一系列等间隔的圆（用R表示圆的半径），形成一系列的同心圆环。

（4）以lnR为横坐标，lnN为横坐标，N为圆半径R范围内的像素数（即将二值图内的所有的1值相加），做出R和N的双对数曲线lnR～lnN，则该曲线的斜率为凝聚物的分形维数，如图7所示。利用该方法，得到图5、6、7沉积物的分形维数分别为1.721、1.749和1.759[9]。该结果与 DLA模拟结果1.67的值相差不大。

图8 分形图的二值化处理

图9 半径R与像素数N的双对数曲线

4 非线性聚集生长理论的应用研究

4.1 在大气颗粒物研究中的应用

大气颗粒物的形成过程就是一种常见的非线性聚集生长过程[12－14]。目前利用非线性聚集生长理论研究大气颗粒物方面，主要包括利用聚集理论探索大气颗粒物的形成过程，分析大气颗粒物的分形特征和物理结构，推断大气颗粒物的粒子来源，分析粒子来源的种类等。研究表明，许多大气颗粒（如煤烟、灰尘）的形成过程与DLA模型或CCA模型的形成过程相似，形成的颗粒物通常具有分形结构。因此，通过分析大气颗粒物的分形特征，不但可以深入探讨大气颗粒物形成的物理机制，还可以了解不同颗粒物的相关物理特性，如大气颗粒物的粒度分布、表面特征等。研究还表明，不同条件下凝聚得到颗粒物，虽然一般具有分形特征，但其分形维数和分形结构却不完全相同[12]。因此，通过比较不同颗粒物的分形维数和分形结构等方面的差异，有助于推测颗粒物的形成环境，了解颗粒物粒子源的相关信息等。另外，大气颗粒物对人体的危害与其分形结构有关，因此，通过对颗粒物的分形特性的分析还有助于了解颗粒物的致毒效应等。

4.2 在薄膜生长研究中的应用

薄膜生长也是一种常见的非线性生长过程，薄膜形成的早期阶段一般包括粒子在衬底上的沉积、簇或岛的形成和长大，以及相互连接形成的连续性结构，其中形成薄膜的晶粒尺寸、晶粒对电子迁移阻力的大小等，都对薄膜的生长过程以及薄膜性能的好坏产生重要影响。因此，非线性生长理论的研究对于揭示薄膜生长的物理过程有着重要的指导意义。主要表现在于以下几个方面[15－18]：（1）从原子或者分子的尺度模拟薄膜的结构和行为，动态显示薄膜的生长过程；（2）分析环境因素对成膜生长的影响；（3）从原子、分子的尺度分析各种环境中成膜生长的物理机制；（4）在一定程度上有助于了解由于实验条件所限造成的薄膜生长过程中的“黑箱”生长，揭示实验中影响薄膜生长的各种客观因素，从而能更好地开展实验工作，节约实验成本和提高实验效率。

[1]谢云霞，罗文峰，李后强.大气颗粒物的分形特征[J].世界科技研究与发展，2004，26（6）：24－29.

[2]杨维，麻凤海，于广明.污水聚合物形成的分形动力学行为[J].辽宁工程技术大学学报，2003，22（5）：714－716.

[3]谢刚，张郑，陈书荣，等.点阴极下金属电沉积过积枝晶二维生长的计算机模拟[J].科学权术与工程，2003，4（3）：343－346.

[4]黄琼，赵珊茸.枝晶研究有发展现状[J].人工晶体学报，2002，31（5）：486－489.

[5]刘方昀.基于 Monte Carlo方法横拟薄膜生长[J].大学物理实验，2008，30（2）：4－7.

[6]T.A.Witten and L.M.Sander.Diffusion－Limited Aggregation a Kinetic Critical Phenomenon[J].Phys Rev Lett，1981，47（19）：1400－1403.

[7]P.Meakin.Formation of Fractal Clusters and Networks by Irreversible Diffusion－Limited Aggregation[J].Phys Rev Lett，1983，15（13）：1119－1122.

[8]P.Meakin.Diffusion－controlled cluster formation in 2－6dimensional space[J].Phys Rev A，1983，27（3）：1495－1507.

[9]陈乐，庞寿全.阴极形状对电解沉积生长影响的实验研究[J].广西物理，2011，32（4）：14－17.

[10]M.Muthukumar.Mean Field Theory for Diffusion－Limited Cluster Formation[J].Phys Rev Lett.1981，50（11）：839－842.

[11]P.Meakin.Diffusion－controlled cluster formation in two there and four dimensions[J].Phys Rev A1983，27（3）：604－607.

[12]疏学明，方俊，申世飞，等.火灾烟雾颗粒物凝并分形特性研究[J].物理学报，2006，55（9）：4466－4471.

[13]谢云霞，罗文峰，李后强.大气颗粒物的分形结构[J].世界科技研究与发展，2004，12：24－28.

[14]陈乐，翁甲强.局部区域粒子源与凝聚集团关系的模拟[J].计算物理，2012，30（5）：161－169.

[15]蒋良俊.计算机模拟半导体薄膜生长的初步研究[D].浙江大学，2001.

[16]杨春，李言荣.薄膜生长模型与计算机模拟[J].功能材料，2003，3（34）：247－249.

[17]胡昌奎.光学实验计算和仿真平台的构建[J].大学物理实验，2011（1）：69－73.

[18]刘丽君.数字像面全息与同轴全息实验研究[J].大学物理实验，2011（6）：19－21.