电力系统稳定器对低频振荡抑制效果的研究

李昂

（陕西理工学院 电气工程学院，陕西 汉中 723003）

电力系统运行时，在负荷突变等小扰动的作用下，发电机转子之间会发生相对摇摆，这时电力系统如果缺乏必要的阻尼就会失去动态稳定。由于电力系统的非线性特性，动态失稳表现为发电机转子之间的持续的振荡，同时输电线路上功率也发生相应的振荡，影响了功率的正常输送。由于这种持续振荡的频率很低，一般在0.2～2.5 Hz之间，故称为低频振荡。低频振荡在国内外均有发生，通常出现在远距离、重负荷的输电线路上，或者互联系统的弱联络线上，在采用快速响应高放大倍数励磁系统的条件下更容易出现。

目前，电力系统普遍采用在励磁调节器上附加电力系统稳定器（PSS）的附加励磁控制方案。它能有效地增强发电机励磁系统的阻尼，抑制低频振荡的发生，是提高电力系统动态稳定性的最经济和最有效的的措施。PSS在国内外得到了广泛应用，我国新投运的大中型发电机组都要求安装PSS[1]。本文介绍了低频振荡的产生机理及发电机附加励磁控制对低频振荡的抑制原理，通过对一个典型的单机—无穷大系统在不同扰动方式下的动态过程仿真，说明了附加励磁控制对电力系统动态稳定性的影响。

1 低频振荡产生机理

一般认为，发生低频振荡的主要原因是现代电力系统中大容量发电机的标幺值电抗增大，造成了电气距离的增大，再加之远距离重负荷输电，造成系统对于机械模式（其频率由等值发电机的机械惯性决定）的阻尼减少了；同时由于高放大倍数的快速励磁系统提供的附加励磁电流在相位上滞后于转子角的变化，进一步加重了负阻尼的状况，即对振荡的阻尼起了相反的作用，也就是所谓的“负阻尼”作用。

大型同步发电机励磁系统一般由励磁功率单元和励磁控制部分（励磁调节器）两部分组成。由于励磁调节器按照发电机端电压偏差进行调节，也称为自动电压调节器（AVR），它是励磁主控制器。随着自动化技术的发展，调节器的调压精度越来越高，励磁电源的响应也越来越快。快速励磁系统的确能够改善同步转矩，从而提高系统在第一摇摆周期的暂态稳定性。然而，快速励磁系统一般是高放大倍数的负反馈系统，它对第一摇摆周期以后系统振荡的阻尼影响很小，有时甚至减小系统对振荡的阻尼。在系统呈现负阻尼特性时，快速励磁系统（特别是高放大倍数时）通常是增大负阻尼，从而恶化系统的运行情况[2]。

并不是所有励磁装置都产生负阻尼，理论和实践都证明，在远距离重负荷输电的单机—无穷大系统完整的线性模型（又称Phillips-Heffron模型，如图1所示）中，由于可能变负值，并且由于高放大倍数快速响应励磁系统的存在，可能导致系统中的阻尼为负，一旦此负阻尼比发电机阻尼绕组、励磁绕组的正阻尼和机械正阻尼还强，则系统在频率扰动下可能出现振荡失稳。这时如果实际存在的发电机电气的和机械的正阻尼较小，则该系统可能发生低频振荡[3]。

图1 单机-无穷大系统Phillips-Heffron模型Fig.1 Phillips-Heffron model of single machine-infinite bus system

式中：xe、vc分别为发电机与系统间的联系电抗、系统母线电压；其余为发电机参数和运行变量。

2 电力系统稳定器的工作原理

重负荷、高放大倍数的快速励磁系统是引起低频振荡的主要原因。因此，当出现低频振荡，可以通过减少输送容量，增强网架结构（使K5>0），或者退出快速励磁系统，改用手动或常规励磁调节器来处理。但前者不经济，后者不利于大扰动下的暂态稳定，因此最根本的方法是设法引入一个附加的阻尼力矩，这可以通过设置电力系统稳定器PSS来解决。

PSS是一种附加励磁控制，其实质是提供励磁系统一个附加信号，通过励磁系统去增加发电机的阻尼转矩。它可以使用发电机转子速度、加速功率或系统频率，以及这些信号的组合作为输入信号。PSS具有物理概念清晰、现场调试方便、现场工作人员易于接受掌握等优点。

图2给出PSS传递函数框图。PSS装置包括信号处理单元、隔直单元、超前—滞后单元、放大单元和限幅单元。系统中的振荡信号通过PSS时经信号处理单元滤波后接入隔直单元；隔直单元滤掉小于等于0.01 Hz的直流次要信号，该单元只有输入的频率大于0.01 Hz时才输出信号，否则自动闭合，处于待命状态；超前—滞后单元补偿传感器、高频滤波器及其它单元对主要信号所造成的相位滞后，该单元根据需要可以有不同的级数；放大单元将补偿后的信号放大；限幅单元的作用是防止故障时发电机的机端过电压。

图2 PSS通用框图Fig.2 Ordinary block diagram of PSS

图中：K 为增益，Tw为隔直环节的时间常数，T1、T2、T3、T4为超前—滞后环节的时间常数。

若取Δω为PSS输入信号，其传递函数为GPSS（s）=GPSS＜ΦPSS。PSS输出VPSS作为励磁附加控制信号，由图1可知附加的阻尼力矩为

若使 GPSS（s）的超前相位 ΦPSS恰好等于式（2）分母的相位Φ3，则

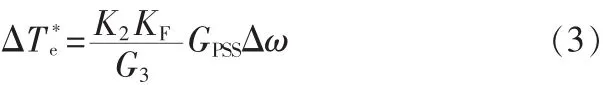
以Δω为输入信号的PSS使用的是超前网络，超前网络在高频段增益变大，所以对发电机扭动振荡极为敏感，使扭动振荡更加严重。以ΔP作为输入信号，检测方便，所需超前角度小，稳定性好，已得到广泛应用，但存在反调现象。以ΔP和Δω同时为输入信号，它们可以相互补偿，减小反调现象的影响[4]。本文就以ΔP和Δω同时作为输入信号的PSS（如图3所示，图中Kp为功率增益、KΔ为频率增益）加以探讨。

图3 输入信号为ΔP+Δω的PSS框图Fig.3 Block diagram of PSS in ΔP+Δω input

图4 PID励磁控制传递函数框图Fig.4 Transfer function of PID excitation control

3 附加励磁控制对抑制低频振荡的仿真

3.1 励磁控制系统模型

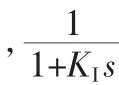
为了保证问题研究具有普遍性，本文选择了典型的单机一无穷大电力系统，如图5所示。该系统由发电机组、变压器、双回输电线路、厂用电负荷和无穷大系统组成。其中发电机系统由同步发电机、励磁控制系统（AVR+PSS）构成；无穷大系统由12 000 MVA电源和500 MVA负荷复合而成。同时依据问题研究的侧重点，忽略原动机的出力变化，供给同步发电机恒定的机械功率。选择Step（阶跃）函数作为信号源；PID环节、限幅环节、PSS环节为封装子系统。仿真参数设置：Start time为 0，Stop time为 30；Solver options为 Variable-step和 ode23tb（stiff/TR-BDF2）；Relative tolerance 为 1e-3，其他参数为默认参数。

图5 单机-无穷大系统模型Fig.5 Single machine-infinite bus system

3.2 暂态过程仿真

搭建好图5所示的仿真模型后，并将故障功能模块参数设置后，对系统在大扰动和小扰动下的稳定运行能力进行模拟仿真。

3.2.1 小扰动仿真

在t=14 s时，发电机机端电压参考值阶跃5%，进行小扰动仿真。如图6所示的仿真波形来看，励磁控制器表现出了很好的静态稳定性能，功角和转速的扰动波动幅度很小，功角4 s后趋于稳定，功角8 s后趋于稳定。

3.2.2 大扰动仿真

在t=15 s时，升压变压器出线端三相短路，0.1 s后故障切除，进行大扰动仿真。

如图7所示的仿真波形来看，功角在短路故障（大扰动）时迅速减小，故障消除后，由于励磁控制器的调节作用迅速恢复稳定运行（8 s后），转子间的转速也很快趋于同步（15 s后），功率振荡较快平息，低频振荡得到有效抑制。

3.3 仿真结果分析

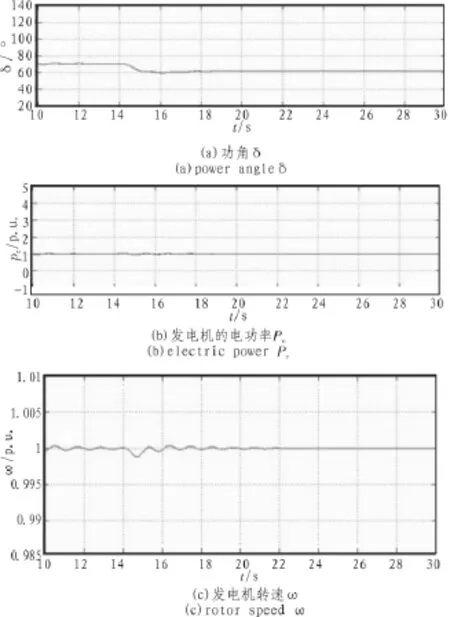
图6 机端电压参考值阶跃时的仿真波形Fig.6 Simulation waves when adding disturbance of 5%

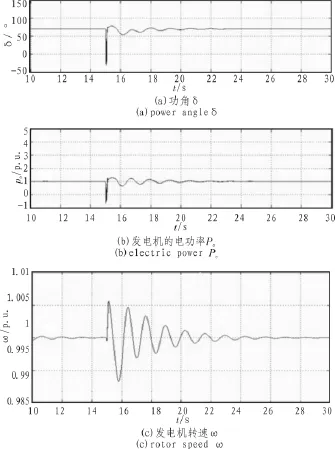
图7 三相短路故障时的仿真波形Fig.7 Simulation waves when fault of three-phase short circuit

由上可见PSS有明显的提高阻尼的作用。无论小干扰还是大干扰，都可以使负阻尼（或弱阻尼）变为强阻尼，且有很好的适应性（鲁棒性），可以满足在各种运行方式下稳定运行的需要。PSS的作用使得发电机产生了附加电磁功率，该附加功率增强了系统的阻尼，使第一次功角振荡回摆的幅度明显减小，明显改善了发电机的运行特性。

4 结束语

电力系统稳定器PSS对于电力系统稳定性的作用程度主要取决于 2点：1）PSS的安装位置；2）PSS的参数[7]。 文中采用以和同时为输入信号的PSS作为励磁附加控制系统，通过对单机—无穷大系统在大扰动和小扰动下的稳定运行能力进行模拟仿真，定性的分析了励磁控制系统对于稳定性的影响。从仿真结果可以看出，PSS可以提供足够的正阻尼，有效克服AVR的负阻尼作用，提高了系统动态稳定性。但是在复杂多机系统中，型号及配置地点的选择是相当复杂且重要的。若选择不当，甚至会使系统低频振荡更为严重[8]。

[1]张茂盛.大型发电机励磁系统浅析[J].山西电力，2007（6）：51-54.

ZHANG Mao-sheng.Analysis of large-scale unit of excitation system[J].Shanxi Electric Power，2007（6）：51-54

[2]王锡凡，方万良，杜正春.现代电力系统分析[M].北京：科学出版社，2003.

[3]姚强.电力系统低频振荡及其抑制方式的研究与仿真[J].电工电气，2010（12）：1-6.

QIANG Yao.Studyand simulation oflow frequency oscillation for power system and its inhibition method[J].Diangong Dianqi，2010（12）：1-6.

[4]楚文斌，刘觉民，刘军志，等.具有新型PSS的励磁系统建模与仿真[J].电机与控制应用，2009（12）:6-25.

CHU Wen-bin，LIU Jue-min，LIU Jun-zhi，et al.Modeling and simulation about included new PSS of excitation system[J].Electric Machines&Control Application，2009（12）:6-9.

[5]李维波.MATLAB在电气工程中的应用[M].北京：中国电力出版社，2006.

[6]相伟，马幼捷，周雪松，等.PID励磁控制对比例式励磁调节效果的改善[J].天津理工学院学报，2004（2）:5-7.

XIANG Wei，MA You-jie，ZHOU Xue-song，et al.The limitation of proportional control and the improvement of PID control of the excitation systems[J].Journal of Tianjin Institute of Technology，2004（2）:5-7.

[7]张帆，李剑峰，王伟，等.基于MATLAB的PSS和SVC对电力传输稳定性的仿真[J].电气开关，2009（1）:40-42.

ZHANG Fan，LI Jian-feng，WANG Wei，et al.The simulation of PSS and SVC to stability of electric power pransmission based on MATLAB[J].Electric Switchgear，2009（1）:40-42.

[8]倪以信，陈寿孙，张宝霖.动态电力系统的理论和分析[M].北京：清华大学出版社，2002.