一种新型粒子滤波算法及其在航天器交会对接相对导航中的应用
李 科,张 骞,龚 彬,刘 伟
(西安卫星测控中心厦门测控站,厦门361023)
1 引言
激光雷达由于激光本身波束窄、相干性好、工作频率高等优点,能在交会对接过程中,提供高精度的相对距离、速度、角度和角速度的测量,因此,激光雷达作为一种光学敏感器常被用作航天器相对导航。然而,光学敏感器的测量噪声大多呈现厚尾分布的特点,目前相对导航中常采用的EKF[1-3]、UKF 和 GKF[4]等基于线性高斯分布的方法具有一定局限性,对于这种非线性和非高斯分布的测量模型,有可能会引入较大的模型误差。
近年来,基于粒子滤波的方法被频繁引入到航天器导航方面[5-7]。粒子滤波可以用一组加权的随机粒子样本来近似状态的后验密度函数,适用于任何非线性非高斯系统。相比其他方法,粒子滤波在解决航天器导航问题方面具有明显的优势,但是粒子滤波算法仍然存在粒子退化和贫乏问题,国内外许多学者就这方面展开了深入地研究。文献[8]利用传统遗传算法对粒子滤波进行了优化,但是传统遗传算法容易出现早熟现象,从而影响滤波性能;文献[9]在无迹卡尔曼滤波(Unscented Kalman Filter,UKF)中引入量子遗传算法,以减轻粒子匮乏现象对无迹粒子滤波的影响。本文则利用一种云遗传算法和UKF对粒子滤波进行改进,应用在航天器交会对接相对导航中,通过解决迭代过程中的粒子贫乏和退化问题来提高估计精度。
2 基于激光雷达测量的系统方程
激光雷达可以实时测量目标航天器相对于追踪航天器的距离、仰角和方位角。为得到两航天器的相对位置和相对速度的估计值,本文在粒子滤波器的框架内,以UKF作为建议分布,云遗传算法进行重采样,然后进行状态估计。
考虑理想的二体运动情况,即假设地球为均匀圆球体,目标航天器运行于圆形轨道,不考虑轨道摄动,追踪航天器和目标航天器均看做质点,建立如图1所示的相对导航坐标系Oxyz(O1x1y1z1):
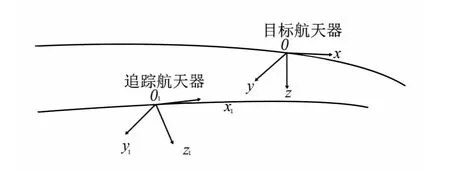
图1 目标航天器和追踪航天器的垂直坐标系Fig.1 Vertical coordinate systems of target spacecraft and tracking spacecraft
其中原点为目标航天器质心,z轴指向地球质心,x轴垂直于z轴,指向轨道角速度方向,y轴与z、y轴构成右手系。追踪航天器相对于目标航天器的运动Hill方程如式(1)所示:
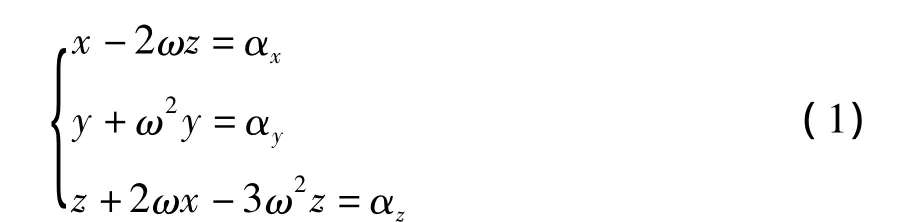
由式(1)得到系统的状态转移矩阵:

系统的状态方程为:
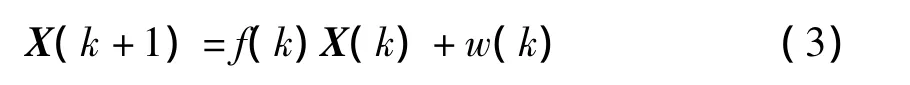
其中w(k)为过程噪声。
激光雷达可提供目标航天器与追踪航天器在01x1y1z1坐标系下的相对距离ρ和相对视线仰角α以及视线方位角β,系统的测量方程为:
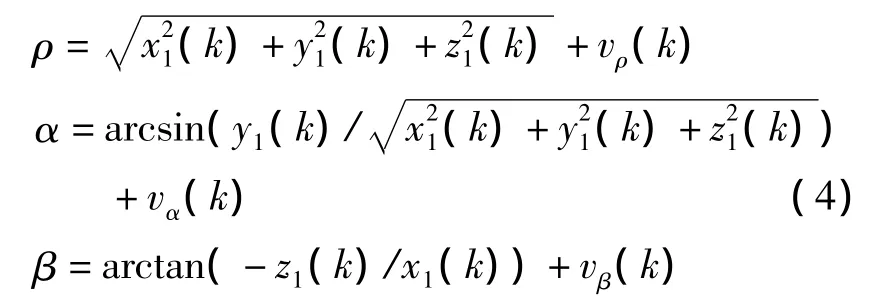
其中vρ(k),vα(k),vβ(k)为测量噪声,服从厚尾分布:

由于系统的状态方程和状态变量是在01x1y1z1坐标系下,而测量方程是在01x1y1z1坐标系下,需要将两个方程中的变量进行统一。考虑到两航天器之间的距离较近(1 km以内),可以认为两个航天器的坐标系是相互平行的,有x=-x1,y=-y1,z=-z1。则系统的非线性测量方程变为:
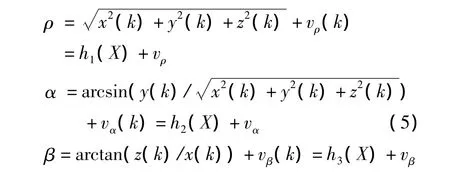
令z(X)=(ρ,α,β)T,v(k)=(vρ(k),vα(k),vβ(k)T则系统的测量方程为:

其中h(X)=(h1,h2,h3)T。
3 UKF算法
在粒子滤波器的框架内,以UKF作为建议分布,充分利用了当前观测数据,使样本与真实后验分布产生的样本更相近,即使似然函数位于系统状态转移概率密度函数的尾部,而且观测精度要求较高时,也能很好地逼近真实后验分布。假设k-1时刻系统的状态及相应协方差的估计分别为和,计算SIGMA点:
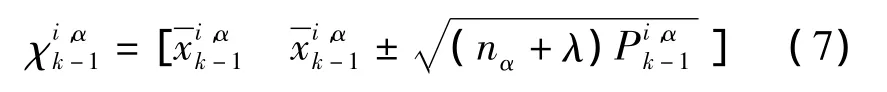
时间更新:

其中和是第j个SIGMA点的权值,nα=nx+nv+nu。
更新预测状态估计量:

其中K=Px~k,z~k为卡尔曼增益,按下面公式计算得到:
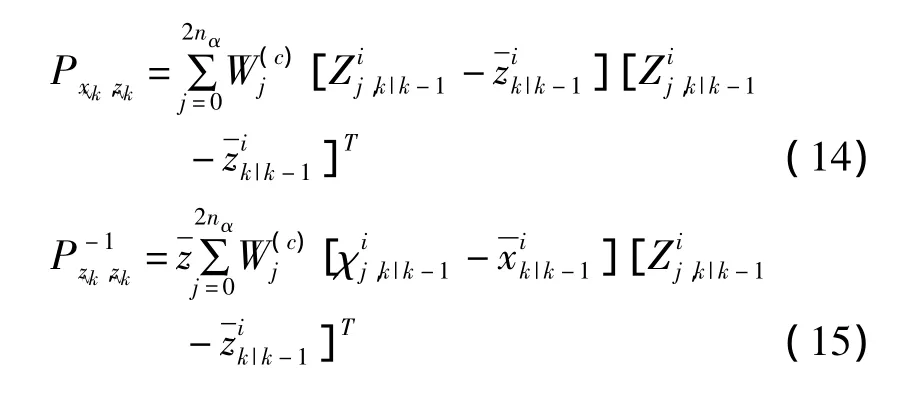
4 云理论与云遗传重采样算法
云遗传重采样从原理上来说,是在粒子滤波的重采样过程中应用云遗传算法中的选择、交叉、变异等操作步骤,对粒子进行优化。常规的GA改进的PF算法,在遗传迭代过程中通过个体之间随机交叉、变异来达到优化的目的,忽略了种群整体的遗传特征。事实上,当前优秀个体的周围往往有存在更加优秀的个体的可能性。云遗传算法[10-11]则利用了正态云模型的随机性和稳定性特点,在考虑当前粒子的观测信息的情况下,利用它发现优胜个体的规则,并利用这个规则指导进化过程,能够提高交叉、变异操作的效率,加快遗传进化的速度,使得遗传进化在群体收敛性和个体多样性之间取得平衡。
4.1 云理论
定义1:假设C属于定量论域U内的定性概念,若定量值x∈U是C上的一次随机实现,且x对C的确定度 μ(x)满足:U→[0,1],∀x∈U,x→μ(x),则在论域U上的分布成为C的隶属云。
当μ(x)服从正态分布时,称为正态云模型。它是随机数的集合,隐含了三次正态分布规律,具有稳定倾向,可以用期望值Ex,熵En,超熵He三个数值特征来表示。

正态云模型是一种泛正态分布,满足N3(Ex,En,He),呈现“中间多,两头少”的特点,即随机性和稳定倾向性,这种分布特点能更近似地描述大部分的客观实际,李德毅等[12]证明了这种正态云模型的普适性。此外,重采样后粒子存在的随机性和倾向后验概率密度峰值的特点,这与云模型云滴具有的随机性和稳定倾向性的特点不谋而合,因此本文采用云模型来近似地对粒子集的后验分布进行描述。
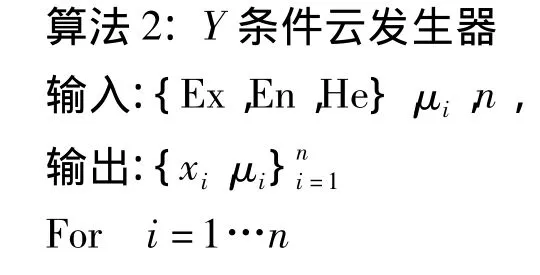
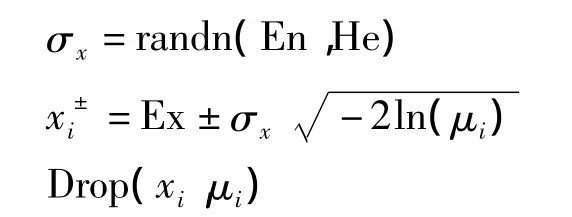
4.2 云遗传重采样算法
在计算交叉概率Pc时,将式(16)中条件输入正态云发生器,生成一个云滴(xi,uc),则这两个个体的交叉概率为Pc=uc。
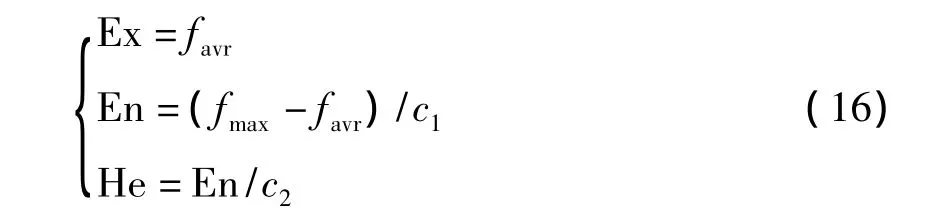
其中:favr为种群平均适应度;fmax为最大适应度;c1、c2为控制参数。
算法3:变异算法
①Ex取原个体;En=变量搜索范围/c3;He=En/c4;μi由个体适应度值确定。其中c3和c4为控制参数,按经验值可取c3=3~6,c4=3~5。
②执行算法2获得和,选择两者中适应度值大的个体作为新个体。
从算法2中可知确定度决定了个体的搜索范围。下面用个体的适应度值通过线性变换来获得其相应的确定度:
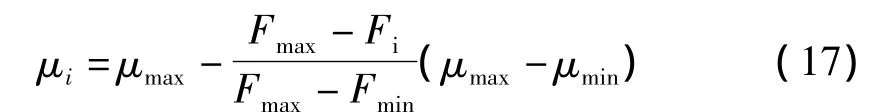
式中:Fmax和Fmin分别表示种群中适应度值最高和最低的个体;Fi和μi分别为第i个个体的适应度值及其确定度;μmax和μmin分别为最大确定度和最小确定度,由经验值决定,本文中μmax=0.95,μmin=0.2。
算法4:云遗传重采样
步骤2.适应度函数计算。将每个粒子的观测概率作为适应度函数,即Fi=p(|)。
步骤3.选择、交叉操作。
步骤4.变异操作。通过MH算法选择可接受粒子:
①在u~[0,1]区间随机均匀抽样;
②随机选取一个旧粒子执行算法3,获得新粒子(t),计算变异后粒子的观测概率p(zk|(i),计算变异粒子接受概率:

③如果u≤α(,(i)),则接受移动:=);否则拒绝移动:=。这样获得新粒子集合
④逐步增大参数和,重复遗传操作,直到误差精度符合要求,令=1/N。
5 基于激光雷达测量的粒子滤波器
假设目标航天器位于轨道高度为380 km左右的圆形近地轨道,轨道角速度很小,噪声之间的耦合可以忽略不计,根据式(3)中给出的系统状态转移矩阵和式(6)给出的测量方程,给定目标的状态空间模型如式(18)。

算法的总体流程图如图2所示:
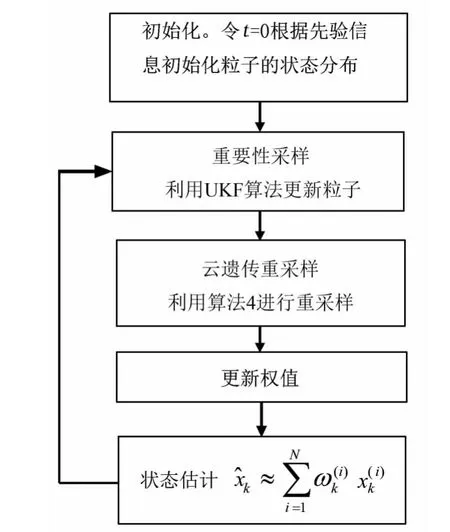
图2 基于激光雷达测量的粒子滤波总体流程图Fig.2 Particle filter overall flow chart based on ladar measurement
具体步骤如下:
步骤1.初始化。根据先验信息p(x0)初始化粒子状态分布
步骤2.重要性采样。fori=1,…,N,根据UKF算法更新粒子:
步骤2.2根据方程 (8)~(11)即式(18),向前传递SIGMA点得到状态及协方差的预测值,根据方程(10)得到状态估计量,根据方程(12)得到预测的测量值的均值;
步骤2.3根据式(14)~(15)求取卡尔曼增益K后,根据方程(13)修正一步预测估计值,获得修正的状态估计。

步骤4.利用算法4进行云遗传重采样。
6 实验与仿真
系统参数设置如下:目标的初始状态X(0)=(2 500,200,5 000,10,-3,1)T,系统的过程噪声协方差为:Q=diag(100,100,100,0.1,0.1,0.1)。
假设测量噪声分布服从厚尾分布,满足:


图3 4种算法的RMSE曲线Fig.3 RMSE curves of four kinds of algorithm

表1 目标位置、速度均方根误差Table 1 Location and speed RMSE of the target

其中,ζ=0.2。
仿真中取粒子数目N=1500;蒙特卡罗仿真次数M=100。图 3 给出了 PF、RPF[6]、UPF、GAPF和CGAPF的相对均方根误差(Root Mean Square Error,RMSE)曲线,表1给出了5种算法的平均RMSE性能评价,从图3和表1可以明显看出:CGPF性能优于PF和RPF、UPF以及GAPF。其中RMSE和平均RMSE定义分别如式(19)与(20)所示:
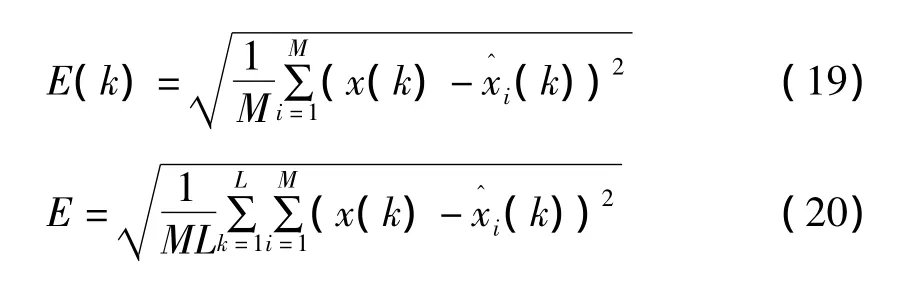
7 结论
本文将UKF和云遗传粒子滤波算法相结合,采用UKF作为建议分布,得到更接近真实的近似分布,在重采样过程中,由于云模型具有的随机性和稳定倾向性特点,对粒子进行了较好地优化,有效地化解了粒子的有效性和多样性之间长期存在的矛盾,提高了跟踪精度,为交会对接相对导航问题提出了一种新的解决方法,但是,由于星载计算机计算能力有限,粒子滤波算法庞大的计算量使得将其应用于航天器自主导航等实际系统中仍然存在困难。
[1] 马鹏斌,王丹.基于EKF和多信息源融合的空间交会对接过程实时定轨方法[J].载人航天,2011,17(3):7-30.
[2] 吴伟仁,王大秩,胡海霞,等.一种环月交会对接航天器的自主导航方法[J].中国科学,2012,42(5):548-555.
[3] 张剑峰,曾国强.扩展卡尔曼粒子滤波在编队卫星相对轨道确定中应用[J].航天控制,2010,8(4):40-45.
[4] Ienkaran A,Simon H.Discrete time nonlinear filtering algorithms using Gauss-Hermite quadrature[J].IEEE,2007,95(5):953-977.
[5] 刘雪奎,孙兆伟,张健,等.基于粒子滤波的通信保障航天器相对导航方法[J].哈尔滨工业大学学报,2012,44(11):27-30.
[6] 周翟和,刘建业,赖际舟,等.Rao-Blackwellized粒子滤波在SINS/GPS深组合导航系统中的应用研究[J].宇航学报,2009,30(2):515-520.
[7] 刘涛,解永春,胡海霞.粒子滤波及其在航天器交会对接相对导航中的应用[J].空间控制技术与应用,2011,37(6):19-27.
[8] 陈善静,杨华,曾凯,等.基于遗传算法的粒子滤波跟踪算法[J].光电工程,2010,37(10):16-21.
[9] 李金,于虹,周璐璐,等.基于量子遗传和无迹粒子滤波的人体运动跟踪[J].系统仿真学报,2008,2(18):4867-4871.
[10] 韩勇,曹兴华,杨煜普.一种改进的自适应云遗传算法[J].计算机仿真,2011,28(10):191-195.
[11] 张飞舟,耿嘉洲,程鹏.基于云遗传算法的公交车辆智能调度[J].武汉大学学报,2010,35(8):905-908.
[12] 李德毅,刘常昱.论正态云模型的普适性[J].中国工程科学,2004,6(8):28-34.

