仓库选址问题的一种混合算法

杨 立

（运城学院公共计算机教学部，山西运城 044000）

仓库选址问题的一种混合算法

杨 立

（运城学院公共计算机教学部，山西运城 044000）

对于一些大型企业来说，科学的仓库布局以及合理的配送方案可以减少物流营运成本，提高企业效率。针对此问题，本文提出一种基于和谐搜索算法和遗传算法的混合算法，并通过实验验证了该算法的可行性和高效性。

选址；分配；和谐搜索算法；遗传算法

伴随着经济的迅速发展和竞争压力的不断增强，企业逐渐意识到，合理地建立分销网络，加强对分销环节的管理，是在当前客户驱动的竞争环境下，提高客户满意度，增强企业竞争力的重要途径[1]，这类选址—分派问题越来越引起大量研究者的关注，而随着计算机技术的高速发展，大规模计算成为可能[2]，很多研究者采用遗传算法[3]、拉格朗日松弛法[4]、模拟退火算法[5]等算法来求解。本文将传统遗传算法与和谐搜索算法相结合，针对问题设计有效的编码方案和遗传算子对此问题进行求解。

1 模型设计

仓库选址及配送方案问题需考虑的现实因素有很多，例如，仓库与分销点之间的距离、地价租金、交通状况、商品运输成本等。本文为方便对问题进行求解，将仓库与分销点之间的距离、交通状况、运输成本等因素量化为配送每单位重量所需要的费用，并进行假设：(1)从已知的若干个备选点中选取其中的某些建设成仓库；(2)一个仓库可以为多个分销点配送；(3)一个分销点仅由一个仓库为其配送；(4)各个分销点的需求量已知。数学模型为：

约束条件：

其中，m为仓库的个数；n为分销点的个数；xij为从仓库i到分销点j配送每单位货物所需费用；yy为从仓库i到分销点j的运输量；ui为第i个仓库的启动费用；Ri为第i个仓库的容量。

式(1)表示总费用最少；式(2)表示对仓库需求量应小于等于其容量；式(3)表示每个分销点仅由一个仓库配送；式(4)表示仓库应覆盖所有分销点。

2 和谐搜索算法简介

和谐搜索算法是2001年提出的、用于求解连续优化问题的一种新颖亚启发式算法，可模拟音乐家在音乐表演过程中探寻优美乐谱的过程[6]。和谐搜索算法试图找到一个能够使目标函数达到最值的解向量，算法参数为和谐记忆大小、和谐记忆选择概率、调节概率par、带宽及调节步长等。算法执行步骤为：

步骤1初始化设置，随机产生和谐记忆矩阵：

其中，N是决策变量的个数。

步骤2 产生新的解向量，x′i=(x′i1，…，x′id，…，x′iD)，其中 x′id遵循以下规则产生：

步骤3 更新和谐记忆矩阵。将新产生的和谐向量的目标函数值与和谐记忆中最差的目标函数值进行比较，若新值优于最差值，则进行替换。

步骤4 循环执行步骤2和步骤3，直到满足结束条件。

3 基于和谐搜索算法和遗传算法的混合算法

遗传算法的整体搜索策略和优化搜索方法不依赖于梯度信息，因此，它提供了一种求解复杂系统问题的通用框架[7]，而和谐搜索算法不依赖变量的初始值，是一种随机搜索算法，且每次迭代中，新的解向量均从所有解向量中产生，算法具有良好的遍历性[8]，故本文将遗传算法与和谐搜索算法相结合。混合算法主要流程如图1所示。

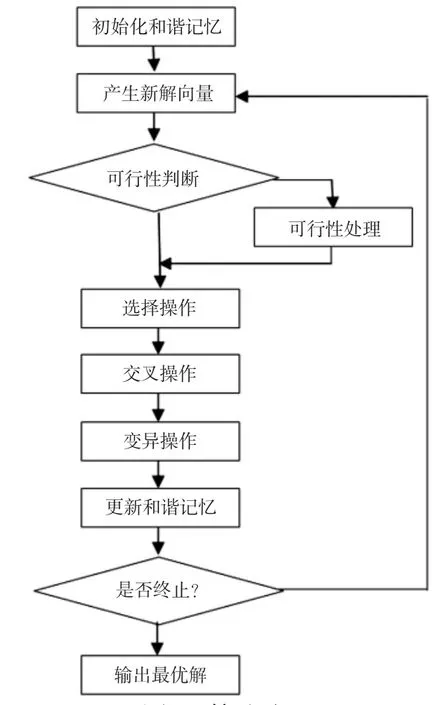
图1 算法流程

3.1 编码方案设计

笔者对传统的编码方案进行改进，传统编码经常采用的是二进制编码，针对仓库选址问题以及相应的分配方案问题，本文采用一种具有双重功能的整数编码方案，即从编码上不仅可以直接得到哪些备选的仓库被选中，而且还可以直接得到分配方案，即哪个仓库为哪些分销点供货。例如，若要从5个备选的仓库中选择其中的若干个为10个分销点进行配货服务，假如得到的解向量为：5-1-4-5-4-4-1-4-5-5，则不仅可以得知1号、4号、5号仓库被选中，而且可以得知分配方案：1号为2号、7号分销点供货，4号为3号、5号、6号、8号供货，5号为1号、4号、9号、10号供货。

3.2 可行性处理方法

对于产生的新的解向量要判断其是否满足本问题的约束条件，若不满足，则要进行可行性处理，具体方法为：首先根据解向量得到具体的仓库编号以及相应的分配方案，然后判断所选仓库的容量是否能够满足分销点的需求量，若不满足，则对分配方案进行调整，将所对应的分销点分配给配货时单位重量花费最少、已被选中且没有达到最大容量的仓库。

3.3 更新解向量

由于和谐搜索算法经常用于求解连续优化问题，而仓库选址问题具有一定的离散性，故在更新解向量时采用遗传算法中的选择、交叉、变异操作进行实现。

4 算例验证

某大型连锁超市要在某市建立若干货物仓库为其分布在市内的50个分销点进行供货服务，经过前期市场考察，已经确定10处备选的仓库地点，并对仓库与分销点之间的距离、地价租金、交通状况、商品运输成本等进行综合考虑，将这些因素量化为从仓库到分销点供货时每单位重量所需费用，并统计出了每个分销点的需求量，如表1所示。每个仓库的容量及相应的建设费用如表2所示。现要确定选择哪些备选地点进行建设以及相应的分配方案，使得总费用最少。

表1 需求量及单位货物运输费用

表2 容量及经费

对于该问题，本文采用以上设计的混合算法，在MATLAB平台下编程实现，参数设置为：最大代数MAXGEN=500，和谐记忆大小HMS=30，和谐记忆概率HMCR=0.6，选择概率PS=0.7，交叉概率PCc=0.7，运行后得到的最优解向量如表3所示，相应的分配方案如表4所示。

表3 最优解向量

表4 分配方案

表5 最优平均值比较

另外，将本文算法与遗传算法分别独立运行10次，并统计得到最优解的平均值，结果如表5所示。可以看出，本文算法的计算效果明显优于遗传算法，其原因在于它不仅具有遗传算法不依赖于问题的具体领域、对问题的种类有很强的鲁棒性等特点，而且具有和谐搜索算法良好遍历性的特点。

5 结语

本文根据仓库选址问题以及分配方案问题，将和谐搜索算法和遗传算法的主要算子进行有机结合，形成一种针对此问题的混合算法，通过算例可以证明，该算法可以有效地解决问题。

[参 考 文 献]

[1]税文兵,叶怀珍,张诗波.物流配送中心动态选址模型及算法研究[J].计算机应用研究,2010,27(12):4476-4479.

[2]王喆.基于组合遗传算法的铁路危险货物办理站点整合优化[J].计算机应用,2010,30(9):2301-2304.

[3]周兴龙,金鹏飞.基于遗传算法的单点物流选址问题探析[J].物流工程与管理,2010,3(27):39-42.

[4]王文峰,刘新亮,郭波.综合多准则决策的保障设施选址—分派方法[J].系统工程理论与实践,2008,28(5):148-155.

[5]秦进,史峰.物流设施选址问题的双层模拟退火算法[J].系统工程,2007,25(2):36-40.

[6]韩毅,蔡建湖,周根贵,等.废弃物处理站选址问题的和谐搜索算法[J].计算机科学,2011,38(6):255-258.

[7]侯晓峰,薛惠锋.遗传算法在城市污水处理厂污泥处理处置项目选址中的应用[J].上海交通大学学报,2011,45(7):1080-1084.

[8]骆乾坤,王佩,朱国荣.水文地质参数识别的快速和谐搜索算法[J].水文地质工程地质,2011,38(4):14-19.

A Hybrid Algorithm for the Problem of Warehouse Location

YANG Li

(Public Department of Computer Teaching,Yuncheng University，Yuncheng Shanxi 044000，China)

For some large enterprises,scientific warehouse layout and reasonable distribution scheme can reduce logistics operation cost,and improve the efficiency of enterprises.In view of this question,this paper proposes a hybrid algorithm which is based on the harmony search algorithm and genetic algorithm,and show that the algorithm is feasible and efficient by experiments.

location；distribution；harmony search algorithm；genetic algorithm

TP301.6

A

1008-178X(2013)01-0021-04

2012-12-23

2011年运城学院院级项目（YQ-2011076）。

杨 立（1978-），男，山西运城人，运城学院公共计算机教学部讲师，硕士，从事计算机应用与人工智能研究。