由Langmuir方程计算标准吸附平衡常数*

周学永 周鑫

(1天津农学院食品科学系 天津300384;2华中师范大学化学学院 湖北武汉430079)

Langmuir方程是由美国物理化学家Langmuir根据分子运动理论和单分子层吸附的假定推导得出的［1］，其表达式为:θ=bp/(1+bp)。Langmuir方程是描述吸附平衡行为的一种应用最广泛的模型［2］，其使用范围已由当初的气-固吸附逐渐推广至液-固吸附过程，涉及环境、材料、催化等众多研究领域。在Langmuir方程中，参数b被定义为吸附速率常数ka与解吸速率常数kd的比值，即吸附平衡常数。长期以来，人们习惯用吸附平衡常数b进行吸附热力学参数计算，常用公式为:

本文作者认为，这种计算方法是不正确的，理由有如下两点。第一，Langmuir方程中的b虽然是吸附平衡常数，但b不是无量纲量(量纲一的量)［6］。因此它不是标准吸附平衡常数，当然也就不能用于热力学参数的计算。根据国际纯粹与应用化学联合会(IUPAC)的规定，标准平衡常数的定义为:KƟ=exp(-ΔGƟ/RT)［7］，式中 ΔGƟ、R 和 T 的单位依次为 J·mol-1、J·mol-1·K-1和 K，显然，KƟ应是无量纲量(量纲一的量)。第二，从数学的角度而言，在超越函数(如对数、指数、三角函数等)运算中，只有在参数为无量纲量(量纲一的量)时才有意义［8］。由于Langmuir方程中的b不是无量纲量，因此，ln b这种表示方法在数学上没有意义。

由于b是否为无量纲量的问题长期被忽略，导致b的单位在文献中有多种表述，而在进行热力学参数计算时却忽略了这些单位的差别。例如，有文献将 b(有时也写作 Kb)的单位表示为 L·mol-1［9-10］、L·mmol-1［11-12］、L·g-1［13-14］或 L·mg-1［15-16］。而用这些不同单位的 b 计算得出的标准自由能，其单位却都用kJ·mol-1表示，这显然是不应该的。如Bulut等［9］研究了榛子壳和杏仁壳对重金属离子的吸附，利用Langmuir方程对吸附数据进行拟合，获取不同温度下的参数b，采用ΔGƟ=-RT ln b计算吸附热力学常数，结果列于表1。

表1 榛子壳和杏仁壳吸附Ni(Ⅱ)的热力学参数(引自文献［9］)

在298K条件下，榛子壳吸附Ni(Ⅱ)的ΔGƟ计算过程列举如下:

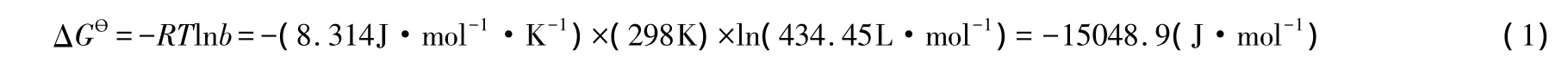
由于b不是无量纲量，故式(1)不符合IUPAC的规定，也不符合数学原理，因此，这种运算方式是错误的。

又如于丽娜等［11］研究了球状壳聚糖树脂对重金属离子的吸附热力学，用Kb代替b进行热力学计算，结果列于表2。在303K条件下，吸附自由能的计算过程如下:

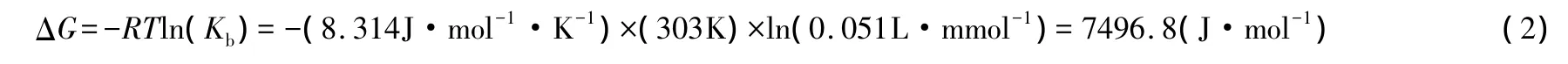
在式(2)中，平衡常数的单位为L·mmol-1，因此，表2中ΔG的计算结果是错误的。

表2 球状壳聚糖树脂对重金属离子的吸附热力学(引自文献［11］)

再如Unuabonah等［13］研究了改性高岭土对Pb(Ⅱ)和Cd(Ⅱ)的吸附特性，吸附平衡常数b和吸附自由能ΔG的计算结果汇于表3。

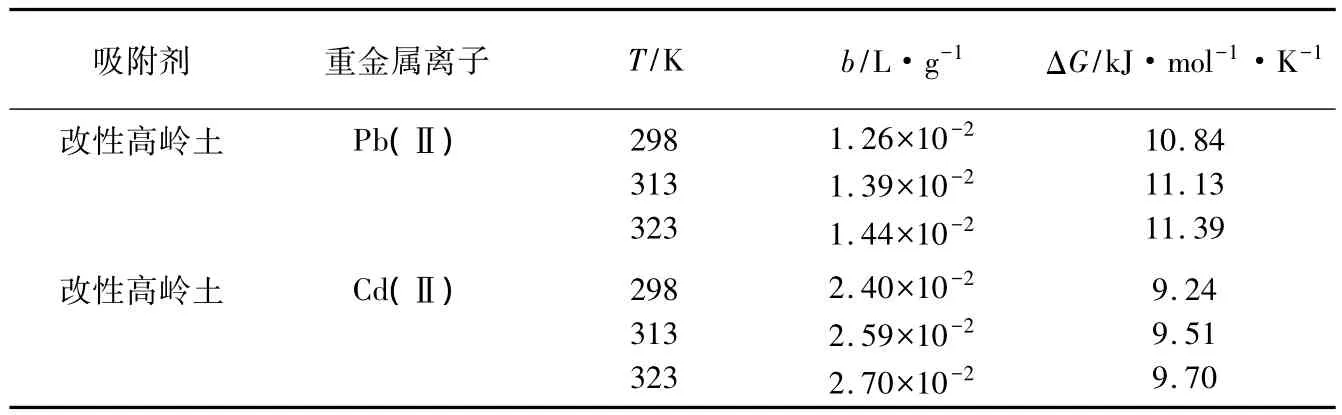
表3 改性高岭土吸附Pb(Ⅱ)和Cd(Ⅱ)的热力学参数(引自文献［13］)

由表3可知，原文作者将ΔG的单位误写成kJ·mol-1·K-1。接下来我们再核查他们的计算过程。在298K条件下，改性高岭土吸附Pb(Ⅱ)的自由能按下式计算:

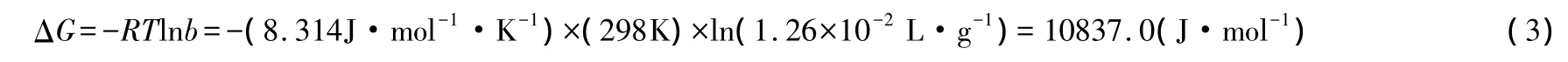
由于b的单位是L·g-1，故表3给出的计算结果是错误的。

除上述所列举实例外，在文献中还发现了其他两种表示平衡常数K的方式。文献［17］用Kb表示Langmuir方程中的经验常数，而计算自由能时却用Kb的倒数表示平衡常数K，即:ΔG=-RT ln K，K=1/Kb，K的单位是 mg·mL-1。文献［18］则用 Langmuir方程中的平衡吸附量 qe(mg·g-1)与b(L·mg-1)的乘积表示平衡常数Ka，并利用下式计算自由能:的单位是L·g-1。

在文献中，类似的错误还有很多。通过上述例证分析可知，b的单位在文献中使用得非常混乱。对于一个特定的吸附过程而言，b用L·mol-1、L·mmol-1、L·g-1或L·mg-1表示，在数值上会有很大差别，计算得出的自由能也会有很大不同，因此，不加限定地使用b进行热力学参数计算，是不妥的。本文从Langmuir方程的推导入手，通过量纲分析阐述参数b是经验吸附平衡常数而不是标准吸附平衡常数的根据。在此基础上，提出利用Langmuir方程计算标准吸附平衡常数的方法，可解决吸附热力学参数计算过程中存在的量纲问题。

1 Langmuir方程的推导及量纲分析

经典Langmuir方程是由气体在纯净固体表面发生吸附这一假定条件下推导得出的，在吸附达到平衡之前，固体吸附剂表面存在空白位点，气体分子可以直接与空白位点结合而发生吸附:

式中A代表气体，S代表固体表面;ka和kd分别为吸附和解吸速率常数。

若以θ表示任一瞬间固体表面被气体分子覆盖的分数，以N代表固体表面具有吸附能力的总的吸附位点数，则吸附速率与气体压力p及固体上的空位数(1-θ)N成正比，吸附速率ra的表达式为［19］:

为了比较转移支付在中国教育水平趋同中的作用，下文将采用β绝对收敛、β条件收敛对中国以及东、中、西部地区间的教育水平进行研究，以揭示西部地区受教育水平差异及缩小的内在原因。中国各省的教育水平和转移支付都存在显著的空间效应，因此本文借助空间经济收敛模型，构建教育水平的空间β绝对收敛(式2～式3)和条件收敛的空间面板自相关模型和空间面板滞后模型(式4～式5)，以考察转移支付条件下教育水平增长与初期发展水平的关系。鉴于教育发展程度除了受国家财政支持力度的影响外，还取决于当地的经济发展水平，因此将经济发展水平也作为必要条件纳入β条件收敛模型。

气体的解吸速率与被吸附的气体分子数目Nθ成正比，即:

当吸附达到平衡时，吸附速率与解吸速率相等，解得:

式(7)即为Langmuir方程，其中p为气体压力，单位为Pa;b=ka/kd，为吸附平衡常数，单位为Pa-1。

同理，将单分子层吸附这一假定应用于液-固吸附过程，便可推导出描述该过程的Langmuir吸附等温式:

式中c为溶质浓度，在不考虑溶液标准态的情况下，c可以用ρ(质量浓度)代替;b为吸附平衡常数，其单位为L·mol-1(使用浓度时)或L·g-1(使用质量浓度时)。

2 由Langmuir方程计算标准吸附平衡常数的方法

标准吸附平衡常数与经验吸附平衡常数之间存在着密切联系，如果将式(7)变形，即可求得气-固吸附过程中经验吸附平衡常数b的表达式:

对一个特定的气相反应来说，标准平衡常数KƟp可以用下列通式表示:

式中B代表反应过程中的任一组分，νB为化学计量系数，pƟ是气体的标准状态压力(101.3kPa)。

依据上述原理，将气体的标准状态压力引入式(9)，即可求得气-固吸附过程中标准吸附平衡常数bƟ的表达式:

对式(11)进行整理，得:

式(12)为考虑气体标准状态时的Langmuir方程，bƟ为标准吸附平衡常数，为无量纲量。

同理，将溶液标准态引入液-固吸附过程，可以得到修正的Langmuir方程:

式中c为溶质浓度，单位为mol·dm-3;cƟ为溶液的标准态浓度(1mol·dm-3);bƟ为标准吸附平衡常数，单位为1。值得指出的是，当考虑溶液的标准态时，须使用浓度(单位为mol·dm-3)，这就相当于对溶质浓度的单位进行了规范和限定。

3 讨论

如何利用Langmuir方程中的参数进行正确的热力学计算，是化学工作者应当认真考虑的问题。这个问题本来并不困难，可能是由于受思维定式的束缚以及习惯引用他人文献的做法，不少人忽视了Langmuir方程中原有的某些假定条件，致使出现了将经验平衡常数误用为标准吸附平衡常数的现象。在经历了较长时间的探索后，我们认识到，忽略平衡常数的量纲是导致自由能误算的根本原因，这促使我们写出本文，推导用Langmuir方程计算标准吸附平衡常数的公式。

［1］Langmuir I.J Am Chem Soc，1918，40:1361

［2］Rossi C G，Heil D M，BonumàN B，et al.Environ Model Software，2012，38:40

［3］Donnaperna L，Duclaux L，Gadiou R，et al.J Colloid Interface Sci，2009，339:275

［4］Vinod K G，Imran A，Vipin K.J Colloid Interface Sci，2007，315:87

［5］张再利，况群，贾晓珊.生态环境学报，2010，19(12):2973

［6］Zhou X，Liu N，Gao J，et al.Int J Chem Reactor Eng，2011，9:A5

［7］International Union of Pure and Applied Chemistry Physical Chemistry Division.Quantities，Units and Symbols in Physical Chemistry.2nd ed.London:Blackwell Science Ltd，1993

［8］陈长植.工程流体力学.武汉:华中科技大学出版社，2008

［9］Bulut Y，Tez Z.J Hazard Materials，2007，149:35

［10］Das D P，Das J，Parida K.J Colloid Interface Sci，2003，261:213

［11］于丽娜，汪东风，胡维胜，等.中国海洋大学学报，2008，38(1):27

［12］Huang Y H，Hsueh C L，Huang C P，et al.Sep Purif Technol，2007，55:23

［13］Unuabonah E I，Adebowale K O，Olu-Owolabi B I，et al.Hydrometallurgy，2008，93:1

［14］Adebowale K O，Unuabonah E I，Olu-Owolabi B I.Chem Eng J，2008，136:99

［15］Sakkayawong N，Thiravetyan P，Nakbanpote W.J Colloid Interface Sci，2005，286:36

［16］lmeida C A P A，Debacher N A，Downsc A J，et al.J Colloid Interface Sci，2009，332:46

［17］孙培宾，陈江，尹进华，等.化学与生物工程，2011，28(4):62

［18］雒和明，曹国璞，张建强，等.应用化学，2010，27(2):211

［19］Atkins P W.Physical Chemistry.Oxford:Oxford University Press，1978