Thermal Error Analysis in Machine Tools Based on Generalized Interval Bays’rule
XIE Fengyun
School of Mechanical and Electronical Engineering,East China Jiaotong University,Nanchang 330013,China
1.Introduction
Thermal errors affect the accuracy of the workpiece which is produced by on the metal-cutting machine tools considerably.Peklenik proposed the percentage of error from thermal effects will account from 40%to 70%.Recently,plenty of research has been done on thermal errors,such as thermal error compensation,thermal error modeling,and prediction of thermal deformation[1 -2].Although these methods are processed by precise value or precise probability,it does not differentiate aleatory uncertainty that is arised from the physical indeterminacy of the world and epistemic uncertainty is extracted from the uncertain knowledge about its actual state.Recently,a generalized interval Bays’rule(GIBR)[3]which is based on the model interval was proposed.In GIBR,aleatory uncertainty is represented as probability measure;epistemic uncertainty is captured by interval.Model interval can solve aleatory uncertainty and epistemic uncertainty simultaneously,and the calculation could be simplified in applications by Kaucher arithmetic[4].
In this paper,the method to analyze thermal error based on model interval probability is proposed.The prior probability of temperature of machine tools bearing is obtained by experiments in some interval.The posterior probability of unobservable thermal error of machine tools bearing can be obtained by GIBR in some interval.The result is a form of the model interval probability that can improve the reliability of making decision.
2.Generalized interval Bayes’rule(GIBR)
GIBR in the context of the model interval(generalized interval)theory is an extension of the classical Bayes’Rule.Model interval[5 -6]and it is an extension of the classical interval with better algebraic based on the Kaucher arithmetic.A model interval is not constrained by lower and upper probability.For instance,in classical interval,[4,7]is valid interval and called proper,[7,4]is invalid interval and called improper.However,they are allowable in model interval.The relationship between proper and improper intervals is established with the operator du-al as dual.The GIBR is stated that

Where,Ei(i=1,…,n)are mutually disjoint event partitions of sample space Ω andand the boldface symbols are stated the form of model interval probability.
Based on the GIBR,the problem of information assimilation can be solved.Prior probabilities and likelihoods are constructed or solicited.If data are available,we may calculate interval probabilities by statistical methods.If no data are available,domain experts may give estimates of interval probability.If no knowledge is available at all,p=[0,1]can be used.
Suppose the states of one or more variables x1,…,xlat Scale X are not directly observable.Instead,the system can be observed via the variable Y corresponding to the unobservable y at Scale Y.Then p(x1,…,xl|Y)is obtained as:
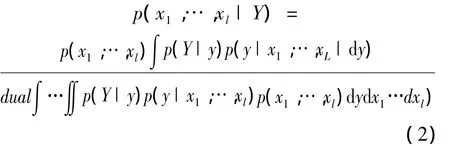
Where,p(y|x1,…,xl)for variables x1,…,xlat scale X and y at scale Y,p(Y|y)for observable Y corresponding to y,and the prior estimate for p(x1,…,xl)[3].
3.Thermal error experiments
In order to experimentally study the thermal error for machine tools bearing,a quasi high-speed feed system experimental bench(HUST-FS-001)was set up.AVM182 linear grating scale with a resolution of 0.5 μm is preferred to measure positioning errors of different positions of the bearing.The Pt100 thermal resistance with a measuring range of 0~150℃and corresponding intelligent thermal resistance modulators are used to measure the temperatures of measuring points.The experimental testing system is shown in Fig.1.
The signals of temperature sensors are obtained by Advantech PCI1716L DA&C cards.Thermal errors were evaluated by the ACCOM software,which was integrated with the VM182 grating scale provided by the Heindenhain Company[7].Experimental data was processed by wavelet de-noising.The temperature of bearing housing and the thermal error of bearing are shown Fig.2 and Fig.3,respectively.

Fig.1 Schematic diagram of testing system

Fig.2 Temperature of bearing housing

Fig.3 Thermal errors of bearing
4.Thermal error model and result analysis
According to formula 4 we can obtain that

where,the posterior probability for p(e|T),the prior thermal error estimate for p(e),the prior conditional probability for p(t|e)and p(t|ec).p(ec)=1-dualp(e),p(tc|e)=1-dualp(t|e),p(tc|ec)=1-dualp(t|ec).
The temperature is divided into two intervals(-∞,8]and(8,+∞),the thermal error is divided into other four intervals,(- ∞,30],(-∞,50],(50,60]and(70,+∞).For ex-ample,assume the observed temperature is T > 8,and thermal error is e>70,the problem is how to calculate p(e>70|T>8)and p(e>70|T>8).
According to the classical Bayes’rule,the data was divided into 10 group of uniform spacing as shown in Fig.2 and Fig.3,p(e>70|T >8)could be obtained as shown in Tab.1.
According to the GIBR,the posterior model interval probability p(e>70|T>8)is calculated by formula 3 and the results are shown in Tab.2.In Tab.2,Interval division‘1’is made of group 1 and group 2 from Tab.2.Interval division‘2’is made of group 1,3 and group 2,3 from Tab.2.Interval division‘3’is made of group 1,3,4 and group 2,3,4 from Tab.2.The prior interval probability and likelihoods will be obtained by the same cyclic iteration.

Tab.1 p(e>70|T >8)based on precise probability

Tab.2 p(e >70|T >8)based on model interval probability
Compare the results between Tab.1 and Tab.2,the amplitude of variation of posterior probability by GIBR is smaller,and thermal error of the posterior probability is more accurate than that of the traditional Bays’rule.In addition,with the group increasing,p(e>70|T>8)is close to real posterior probability value 0.464 8 that can be obtained by recorded data.In addition,the posterior probability p(e|T)will be updated instantly close to true value via GIBR while more prior data are being collected.Furthermore,the posterior probability also will be closer to the true value of engineering while prior interval probability and likelihoods are segmentation.The posterior probability calculation of thermal error is useful for real-time monitoring of the system health and reliability.
5.Conclusions
Uncertainties widely exist in processing of thermal error problem.The traditional thermal error calculation by precise probability has some limitations,such as representing epistemic uncertainty,and inconsistency in the context of subjective probability.In this paper,the proposed model interval is to characterize thermal error of machine tools bearing.Model interval has a capable of processing epistemic uncertainty and aleatory uncertainty simultaneously.To demonstrate the proposed model interval,the posterior probability of machine tools bearing is calculated by GIBR.The results show that the proposed method has a better performance to calculate the posterior probability of thermal error.With two uncertainty components considered simultaneously,model interval form can improve reliability of the results and provide reliable basis for engineering decision-making.In future work,some new algorithms of processed prior data are required,for instance,based on model interval and Hidden Markov model(HMM)may be considered.
[1] XIE Fengyun.A Characterization of Thermal Error for Machine Tools Bearing Based on HMM [J].Machine Tool& Hydraulics,2012,40(17):31 -34.
[2] ZHANG Ting,LIU Shihao.Overview of Thermal Error Compensation Modeling for Numerical Control Machine[J].Machine Tool & Hydraulics,2011,39(1):122-127.
[3] WANG Y.Multiscale Uncertainty Quantification Based on a Generalized Hidden Markov Model[J].ASME Journal of Mechanical Design,2011,133(3):1 -10.
[4] Kaucher E.Interval analysis in the extended interval space IR[J].Computing Supplementa,1980,2:33-49.
[5] Gardenes E,Sainz M A,Jorba L R,et al.Modal intervals[J].Reliable Computing,2001(2):77 -111.
[6] HU Y M,XIE F Y.An Optimization Method for Training Generalized Hidden Markov Model based on Generalized Jensen Inequality[C]//Proceedings of the 9th International Conference on Informatics in Control,Automation and Robotics(ICINCO 2012).2012:268-274.
[7] JIN Chao,WU Bo,HU Youmin.Wavelet Neural Network Based on NARMA-L2 Model for Prediction of Thermal Characteristics in a Feed System[J].Chinese journal of mechanicalengineering,2011,24(1):33-41.
- 机床与液压的其它文章
- Experimental Study on Mechanical Properties of Low Carbon Steel with Ultrasonic Vibration Tensile
- Finite Element Analysis for a New Friction-based Limited-slip Differential Housing
- Precision Measurement of Series Motor Housing Based on CMM
- Wavelet Analysis Fault Information and Realization in Virtual Instrument
- Synchronous Motion Servo-control of Biaxial Cross Coupling Based on Intelligence Fusion Strategy
- Simulation and Optimization Analysis of Circuit Breaker Operating Mechanism

