基于P MA C的步进电机伺服系统的P I D算法研究
张云鹏
(中国电子科技集团公司第四十五研究所,北京 100176)
基于P MA C的步进电机伺服系统的P I D算法研究
张云鹏
(中国电子科技集团公司第四十五研究所,北京 100176)
阐述一种基于PMAC(Programmable Multi-Axis Controller)控制卡的步进电机构成的伺服系统PID(Proportion Integral Derivative)算法。详细的介绍了系统的组成和工作原理,以及PID参数的调节原理和调节方法。我们借助PEW IN TUNING软件,通过分析系统响应曲线,观察系统的稳态特性和动态特性。
可编程多轴控制器;比例、积分、微分(PID);PID算法;伺服系统
在现代工程中,比例、积分、微分控制是一种应用的最为广泛的调节器控制规律,简称PID控制,又称PID调节。PID调节在工业生产过程中的应用自20世纪40年代至今已有70多年的历史,无论结构,原理都十分简单,稳定性好,可靠性高,参数调整方便,已经成为工业控制的主要技术之一。当我们无法正确掌握被控对象的结构和参数,又无法建立准确的数学模型时,其他的控制理论很难得以应用,这时最适合采用PID控制技术。PID调节器引入自整定,根据系统的误差,利用P(比例),I(积分),D(微分)计算出控制量进行控制的。不仅如此,PID调节的鲁棒性可以在一个很宽的范围内变化,保证系统的稳定性,所以在目前得到广泛的应用。但是随着对控制系统的控制精度和响应速度要求的提高,传统PID控制调节对日趋复杂的运行环境缺乏很好的适应性,还有传动机构的扰动,负载的变化等因素的影响,很难得到令人满意的结果。这时人们将PID和模拟自适应,前馈等相结合形成符合控制要求的控制方式。这种组合式的控制算法更能满足各种实际情况的控制要求。本文将阐述一种基于PMAC控制卡的步进电机构成伺服系统的PID算法。
1 系统组成及算法
Deltu Tau Data System公司的可编程多轴运动控制卡Ⅱ型(PMAC2),是一个高性能伺服运动控制器,通过数字信号处理器(DSP),以及灵活的高级语言最多可控制八轴同时运动。PMAC2给多轴控制器提供前所未有的性价比,Motorola的DSP56002是PMAC2的CPU,处理所有八轴的计算。
我们的运动控制系统主要是由工控机,PMAC运动控制卡,步进电机驱动器,步进电机,编码器和运动平台组成。数据处理和驱动控制都由PMAC卡完成,驱动由德国的TRINAMIC步进电机驱动器及其配套电机组成,机械结构为X,Y,Z,θ四向运动平台,反馈检测器件是德国海德汉的旋转编码器。形成了一个由步进电机形成的伺服系统。机构框图如图1所示。

图1 系统结构框图
PID控制,又称PID调节,就是根据系统的误差,利用比例、积分、微分计算出控制量进行控制。模拟PID控制器的原理框图如图2所示,其中r(t)为系统给定值,c(t)为实际输出,u(t)为控制量。调节PID的参数,可以实现在系统稳定的前提下,兼顾系统的带载能力和抗干扰能力,同时在PID控制器中引入了积分项,系统增加了一个零积点,这样系统阶跃响应的稳态误差为零。

图2 模拟PID控制系统原理框图
PID控制器的输入输出关系为:

式中:e(t)为系统偏差,e(t)=r(t)-c(t);
Kp为比例系数;
TI为积分时间常数;
Td为微分时间常数;
比例环节:即时成比例地反应控制系统的偏差信号e(t),偏差一旦产生,调节器立即产生控制作用以减小偏差。
积分环节:主要用于消除静差,提高系统的无差度。积分作用的强弱取决于积分时间常数TI,TI越大,积分作用越弱,反之则越强。
微分环节:能反应偏差信号的变化趋势(变化速率),并能在偏差信号的值变得太大之前,在系统中引入一个有效的早期修正信号,从而加快系统的动作速度,减小调节时间。
目前PC控制系统中所使用的是数字PID控制器,是一种离散的采样控制。通过将模拟PID表达式中的积分、微分运算用数值计算方法来逼近,便可实现数字PID控制。见表1。

表1 模拟PID控制规律的离散化
数字PID控制器的差分方程:

目前数字PID控制器的控制算法通常可以分为位置式PID控制算法和增量式PID控制算法,但是仅有PID控制是远远不够的,因为PID控制是一种反馈控制,既然是反馈控制就一定要有反馈信号,可是从反馈元件得到信号再同命令信号进行比较运算会造成延时。所以现在很多系统引进了前馈控制。采用前馈+反馈相结合的控制结构,既可以达到反馈控制对偏差的控制作用,也可以在干扰引起误差前就对它进行补偿,及时消除干扰的影响。PMAC为用户提供了一个PID位置环伺服滤波器。即PID+速度/加速度前馈+NOTCH滤波的控制环算法。由于前馈调节器不改变系统的稳定性,只对被调量起到补偿作用,因此PMAC卡PID控制加入了速度前馈调节和加速度前馈调节。加速度前馈可以补偿被控对象自身惯性所产生的跟随误差。而速度前馈能减小微分增益或电机阻尼所引起的跟随误差。图3为算法原理图。

图3 PID算法原理图
从图中我们可以看出,比例部分是误差ek与比例系数kp的乘积;微分部分是误差变化量ek
ek-1与微分系数kd的乘积;积分部分在采用了饱和限制后与积分系数ki相乘得到。系统的控制输出是比例,微分,积分这三个部分的代数和,PID算法的实际公式为:

Dout(n)为16位的伺服周期输出命令(-32768到+32767)。它被转换成-10 V到+10 V的输出。它的值由Ix69定义。
Ix08为电机的一个内部位置放大系数(通常设为 96)。
Ix09为电机速度环的一个内部放大系统。
F(n)是伺服周期n内所得的跟随误差,即为该周期内指令位置与实际位置的差值。
V(n)是伺服周期n内的实际速度,即为每个伺服周期最后两个实际位置的差值。
C(n)是伺服周期n内的指令速度,即为每个伺服周期最后两个指令位置的差值。
A(n)是伺服周期n内的指令加速度,每个伺服周期最后两个指令速度的差值。
I(n)伺服周期n的跟随误差的积分,大小为:(在所有的伺服周期内积分都起作用。当CV不等于0时,Ix34=1只关掉了积分器的输入,而没有关掉它的输出。)
2 PID参数调节与设定
通过PMAC卡为用户提供的PEW IN TUNING软件,可以对PID参数进行很方便的调节,进而获得理想的控制性能。PEW IN TUNING为用户提供了两种调节方式,在界面工具栏中点AUTO是自动调节,在工具栏中点INTER是自动调节。自动调节很方便,无需用户自己调节就可以根据运动情况自动获得调节数据,但是只能用于刚性极好的系统,对于刚性较差的,比如传动机构是皮带传动的系统,我们就需要用手动调节来获取较好的PID参数。图4为PMAC的PID调节界面。运行PEW IN软件后,点击工具菜单下的PMAC Tuning就会出现如图所示的调节界面。

图4 PMAC的PID调节界面
3 调整系统反馈增益
在线调试之前要先将I7mn0设成7,使编码器与整个系统构成闭环系统,除此之外,还需要输入ctrl+A指令,这样电机就处于闭环状态了。通过给步进电机一个阶跃信号,观察系统的响应,借助PEW IN TUNING软件得出的曲线及系统性能指标,我们可以了解到系统的响应时间,稳态误差,动态特性。
在软件界面中,包含了主要PID参数:Ix30比例增益,Ix31微分增益,Ix33积分增益,Ix32速度前馈增益,Ix35加速度前馈增益。调节PID参数时,首先应该调P比例增益,即设Ix30比例增益为2000,Ix31微分增益为 0,Ix33积分增益为 0,Ix32速度增益为0,Ix35加速度增益为0。
点Position Step选项,在右边点kill motor after step move选项,在Step move选项里使用默认值Step size(cts)为 1000,Step time(ms)为 500,然后点击Do A Step Move按钮,就会出现脉冲响应曲线。曲线1为指令信号,曲线2为实际位置响应。
从图5中我们可以看出响应曲线的响应时间很长,系统响应缓慢,实际运动曲线和理想的运动曲线位置误差很大,需要继续调试。增大比例增益,其他指标均不变。
如图6所示,当Ix30比例增益增大到8 000时,系统出现了明显的震荡,也有2.4%的超调,造成系统不稳定。虽然上升时间短,响应速度快,但依然不是我们想要得到的效果。
这时将比例增益降低到4 500时,可以看到系统的震荡消失了,超调量为零。这时的Ix30比例增益参数基本满足要求。
许多放大器接受从控制器送来的速度命令,和从电机传送来的速度反馈信号通常由一个测速计或几个旋转变压器得到。使用这些放大器的电机由放大器闭合他们的速度环,而不需要使用PMAC速度环的微分增益,所以我们在PMAC卡上可以不设置微分增益,Ix31设为0就可以了。

图5 参数调节前系统阶跃响应曲线

图6 比例增益增大为8 000时的阶跃响应曲线

图7 调节比例增益后的阶跃响应曲线
速度模式放大器的优点关键是闭合模拟速度环,它们不受量化误差和数字速度环采样频率的限制。这样它们可获得较高的速度环增益,刚性和抗干扰能力。由于这一点,它们可以在很大的切削力下保持精度被广泛地用于机床切削。因为这些高增益,PMAC的位置环比例增益要比其它类型的放大器低得多。
PMAC卡的积分器有两种方式可供选择,由Ix34决定。当Ix34设为1时,积分器在全程都起作用,尽管可以减小跟随误差,但是当运动结束时会过冲,并且系统会不稳定。当Ix34为0时,积分器只在速度为零时起作用。由于PMAC可以调节速度前馈和加速度前馈,所以一般Ix34设为0。这是因为速度前馈和加速度前馈既可以有效的减小跟随误差,又不会损失系统的稳定性。
4 调整系统前馈参数
借助PEW IN TUNING软件,我们可以通过观察正弦曲线响应,调整速度前馈和加速度前馈,进而减小甚至消除系统跟随误差,调整系统的动态特性。打开PEW IN TUNING软件后,点Parabolic velocity选项,在右边点kill motor after step move选项,然后点击Do A Step Move按钮,就会出现正弦响应曲线。
前馈参数的调整方法和比例增益,积分增益的调整方法类似。先调整速度前馈,将Ix35加速度前馈设置为0,然后从零开始,逐步增加速度前馈。
图8为前馈参数调整前的正弦响应曲线,可以看出跟随误差在170 cts(脉冲数),加大速度前馈,减小阻尼造成的跟随误差。
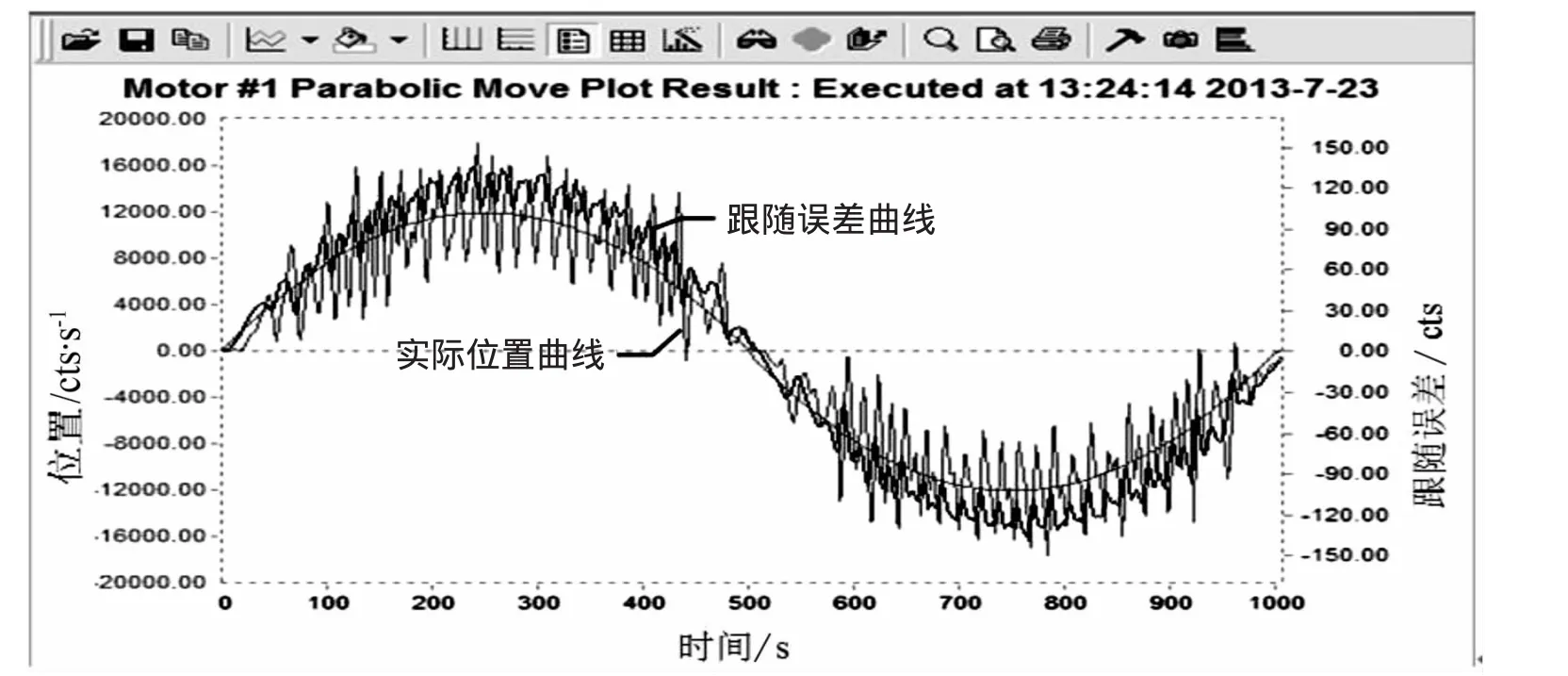
图9 速度前馈Ix32设置为1 000时的正弦波响应曲线
图9为速度前馈Ix32设置为1000时的正弦响应曲线,从图中我们可以明显看出跟随误差减小为120 cts。我们继续调整,增大速度前馈。
当速度前馈增大到6 000时,速度跟随误差出现了反相的情况,这时的速度前馈过大了,我们应该适当的减小速度前馈。
经过一系列的调整,最终将速度前馈参数设置为4 000,这时的跟随误差最小。为了减小惯性造成的影响,下一步我们调整加速度前馈参数。
经过一系列的调整,最后将Ix32速度前馈增益设置为4 000,Ix35加速度前馈设置为4 000,得到跟随误差小且分布均匀的曲线,基本满足使用要求。

图10 速度前馈Ix32设置为6 000时的正弦波响应曲线

图11 速度前馈Ix32设置为4000时的正弦波响应曲线

图12 参数调节后的正弦波响应曲线
5 结束语
整个系统的响应速度,控制精度可以通过PID参数的整定得到很大的提高,通过这种调整,我们可以获得良好的稳态性能和动态特性。借助PMAC提供的PEW IN TUING软件,可以对系统各参数进行调整,并且可以直观的看到各种调试曲线图,最终完成PID参数调整,方便用户使用。
:
[1]北京钧义志成科技发展有限责任公司.PMAC用户手册[Z].
[2]田会峰,刘文杰.基于PMAC的直线电机PID研究[J].自动化技术与应用,2007,26(11):124-126.
[3]韩金恒,潘松峰,高菲,王磊.基于PMAC伺服系统的PID-前馈算法及其参数调节[J].自动控制,2008(5):105-106.
[4]朱立达,朱春霞,蔡光起.PID调节在PMAC运动控制器中的应用[J].控制与检测.2007(2):50-53.
[5]霍罡.可编程序控制器模拟量及PID算法应用案例[M].北京:高等教育出版社.2008.
[6]PMAC/PMAC2 Software Reference Manual[Z].DELTA TAU Data Systems.Inc,2003.
[7]Tranquilla J M,Best S R.A study of the quadrifilar helix antenna for global positioning system(GPS)applications[J].IEEE Trans,AP-38,1990,38(10):1545-1550.
PID Algorithm Research on Step-up Electric Servo System Based on PMAC
ZHANG Yunpeng
(The 45thResearch Institute of CETC,Beijing 100176,China)
Abstract:This paper describes a PID(Proportion Integral Derivative)algorithm which apply to the servo system consisting of a PMAC(Programmable Multi-Axis Controller)control card and stepping motors,which specifies the composition and working principle of the system,and the adjustment principle and adjustment methodology of the PID parameter.PEWIN TUNING software is adopted to observe the static and dynamic characteristics by analyzing system response curve.
Keywords:Programmable multi-axis controller;Proportion integral derivative;PID algorithm;Servo system
2013-07-30
TM383.4
A
1004-4507(2013)11-0042-08
张云鹏(1985-)男,辽宁锦州人,助理工程师,工学学士,现主要从事半导体光刻设备的研究工作。

