考虑红利和退休的最优消费-投资和遗产问题
费为银,何丹丹,朱永王,苏 凯
(安徽工程大学 数理学院,安徽 芜湖 241000)
考虑红利和退休的最优消费-投资和遗产问题
费为银,何丹丹,朱永王,苏 凯
(安徽工程大学 数理学院,安徽 芜湖 241000)
在股票支付红利的情况下,考虑投资者遗产并结合保险,研究3种不同的借贷约束下的消费与投资问题.首先,借助随机微分方程求解投资者最优消费和投资策略的显式表达式,其次,结合数值分析,说明3种约束情形下投资占总财富比率以及消费占总财富比率对于财富的变化趋势,最后,研究了股票是否支付红利对投资比率以及消费比率的影响.
红利;最优投资策略;自由选择退休;随机微分方程;遗产
个人退休的灵活性以及是否能够对未来劳动收入进行借贷显著影响投资者的最优消费以及投资组合策略.文献[1]研究了当经济代理人存在弹性劳动供给时的最优消费投资问题,第一次将劳动闲暇决策加入跨期消费-投资组合选择模型当中,表明了人力资本对最优策略有显著的影响.文献[2]研究了偏好改变情况下的最优投资消费和退休决策问题,经济代理人能够决定酌情停止来作为退休时间,允许代理人的偏好在退休前和退休后能够改变.文献[3]研究了在时间可变的投资机会集下的完备金融市场中,个人投资者的动态消费和投资组合选择.文献[4]研究表明考虑了退休弹性以及能否对未来劳动收入进行借贷显著地影响最优消费-投资策略.
文献[5]研究了在带有习惯形成、随机机会集、随机工资和劳动供给弹性的生命周期模型下的消费-投资和闲暇选择问题,给出了投资者最优消费-投资与闲暇选择策略的显式表达式.文献[6]在Markowitz投资组合策略的框架下,用CVaR代替方差作为风险测度,用几何布朗运动来刻画股票价格过程,得出均值CVaR模型下的动态最优策略和有效前沿边界.文献[7]研究了在考虑股票派发红利的情形下,经济代理人通过不可逆退休时间选择来调整劳动时间框架下最优消费和投资问题.文献[8]考虑了股票支付红利的随机动力学模型.本文在文献[4]的基础上考虑了股票支付红利的情况下,扩展原有模型,得出了在3种约束情形下,考虑保险、红利和退休的消费和投资模型.
1 问题的描述
本文试图建立一个模型,用来分析各种关于消费、投资、退休以及保险的问题.选择问题时做了许多在连续时间金融模型中常见的假设,例如不变的无风险利率、对数正态的风险资产回报等,其他假设看起来似乎并不标准,但是它们对于消费和投资的研究却十分的适合.本文也提供了一些假设,如股票市场投资带有红利分配、死亡率、遗产,此外,投资者在退休之前的劳动收入是带有潜在的随机工资率的,以及投资者可以购买保险,并且获得生命年金等.本文所有的模型考虑的退休是不可逆的,即退休人员退休后不能再从事兼职或者全职工作.
本文主要分析以下3种情形:
(Ⅰ)固定退休期,可以对未来劳动收入进行借贷;
(Ⅱ)投资者自由选择退休期,并且可以对未来劳动收入进行借贷;
(Ⅲ)投资者自由选择退休期,但是不可以对未来劳动收入进行借贷.
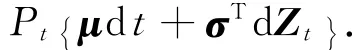
问题 Ⅰ:给定初始财富W0,初始劳动收入y0,给定退休期为T,与退休相关联的示性函数Rt=1(T≤t),选择适应的非负消费{ct},适应的投资组合{θt}(表示投资在风险资产中的投资额),以及适应的非负遗产{Bt},来最大化生命周期消费与遗产的期望效用
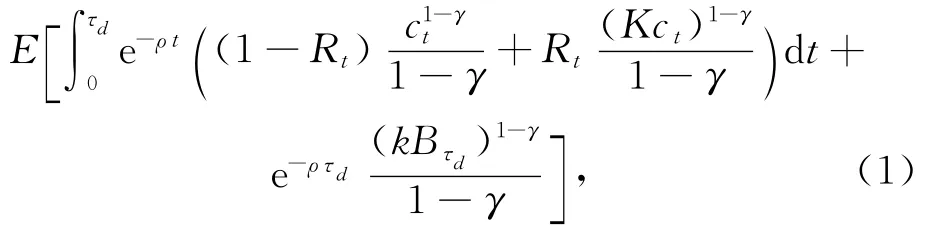
服从于预算约束
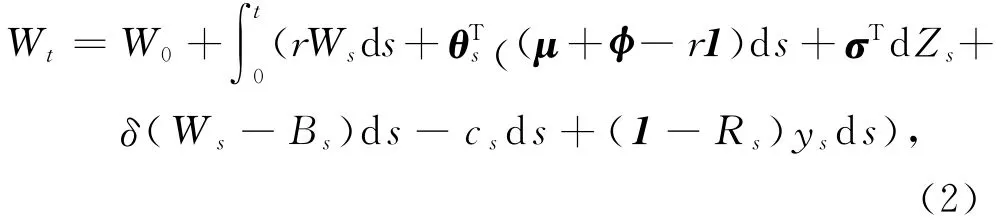
其中:τd为Poisson到达时间;ρ为主观的时间折现率;δ表示Poisson死亡到达率;K和k为消费Ct和遗产Bt的比例;γ为风险厌恶系数;Ws为财富过程;θs为投资组合.
其中劳动收入过程
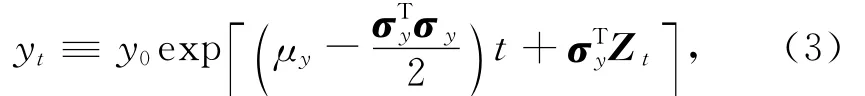
借贷和偿付约束为

其中:
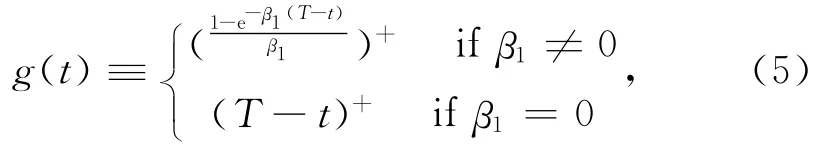
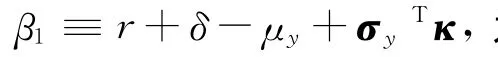
表明投资者在退休期为固定退休期,并且可以对未来劳动收入进行借贷时,投资者的财富与未来劳动收入的折现值之和需大于等于0.
问题 Ⅱ:给定初始财富W0,初始劳动收入y0,初始退休状态R0-,选择适应的非负消费{ct},适应的投资组合{θt},适应的非负遗产{Bt},适应的非降退休示性函数{Rt},为了最大化生命周期消费投资期望效用(式(1)),且服从预算约束(式(2))和退休之前的劳动收入过程(式(3)),借贷和偿付约束Wt为
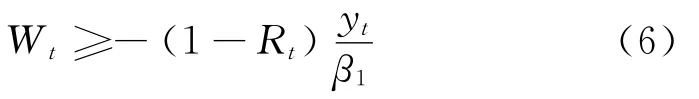
表明投资者可以自由选择退休,并且能够对未来劳动收入进行借贷时,投资者的财富与未来劳动收入的折现值之和需大于等于0.
问题 Ⅲ:条件同问题Ⅱ,但是借贷和偿付约束Wt为

表明投资者可以自由选择退休,但是投资者不能够对未来劳动收入进行借贷时,为了不使得投资者破产,那么投资者的财富必须大于0.
问题的模型采用标准的 Wiener过程Zt,以及用固定风险率δ来表示Poisson死亡到达率,其中Poisson到达时间表示为τd,并且是独立于 Wiener过程Zt.投资者投资两种资产,一种是无风险资产,另一种是风险资产即股票.投资者不仅可以投资无风险资产和股票市场,且可以购买保险,模型中的保险假定由死亡率δ来公平定价,当W-B<0,δ(B-W)表示每单位时间投资者需要支付的保费,并且当投资者死亡是能一次性获得B-W的补偿;当W-B>0,那么δ(B-W)表示一种生命年金的形式,即在投资者死亡之前,都会获得一个现金流来保证生活.假定投资者拥有不变的风险厌恶,且期望效用函数(式(1))采用主观的时间折现率ρ.常数K>1表明对于不工作的偏好,意味着退休过后的边际效用比退休之前的边际效用要大.常数k>0度量了投资者留下大笔遗产的偏好强度,当k1-γ→0表明投资者对于留下遗产没有偏好.
2 最优策略的解析解
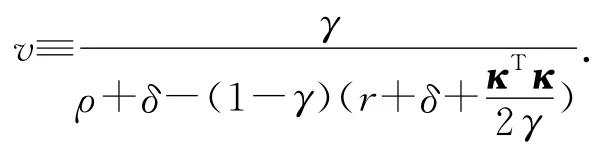
定理1 假定v>0,无需借贷和偿付约束在初始价值下满足严格的不等式

对于问题Ⅰ的解中,最优财富过程为
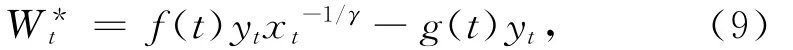
最优消费策略为
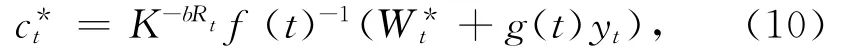
最优投资策略为
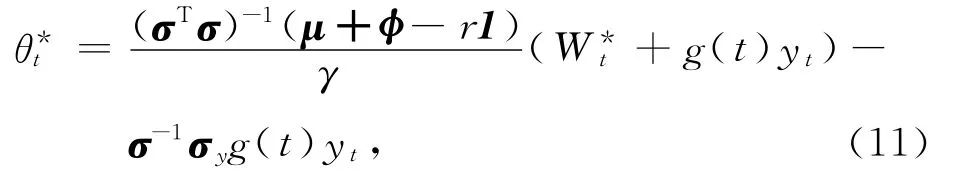
最优遗产策略为
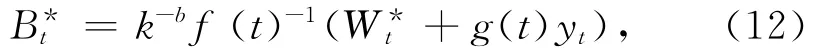
其中
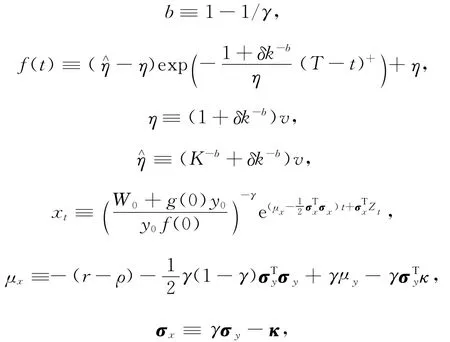
并且,问题的价值函数为
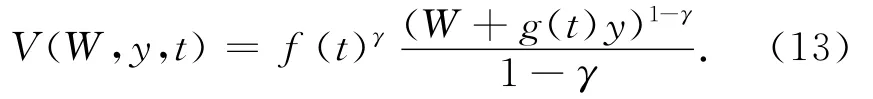
证明 给定式(8),等式(9)中W*是有定义的,容易验证预算约束(式(2))对上述策略是成立的.
定义状态价格密度
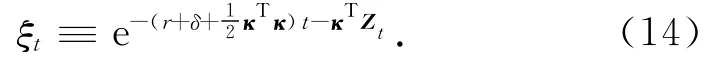
易知g(t)yt是未来劳动收入在t时刻的价值.进一步,未来消费和遗产的现值不超过初始财富
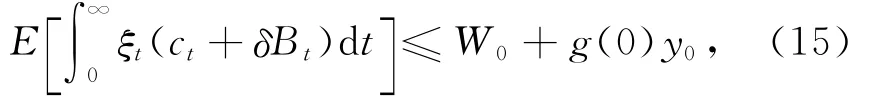
不等式适用于任何可行的策略,在策略是最优的情况下,不等式为等式.
结合死亡风险之后,对于任何可行的策略(c,θ,B)有不等式
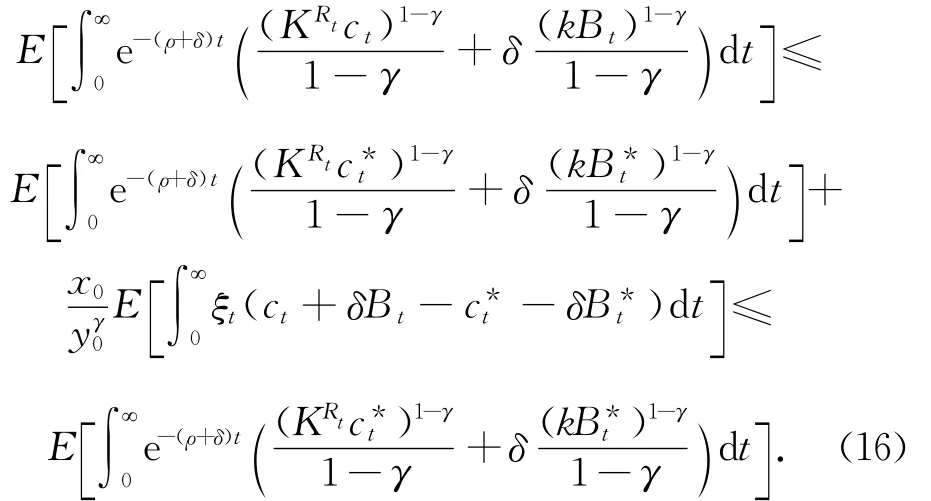
式(16)中第一个不等式为代进以及来进行直接的验证,第二个不等式来自约束条件式(15).在策略是最优的情况下,不等式为等式.以上表明,本文提出的最优策略优于其他策略,之前表明,这个最优策略是可行的,因此定理得证.
不同于问题Ⅰ,采用之前的变量,问题Ⅱ和问题Ⅲ并没有显式解,然而可以构建边际效用的情况下,提出另一种显式解.定义
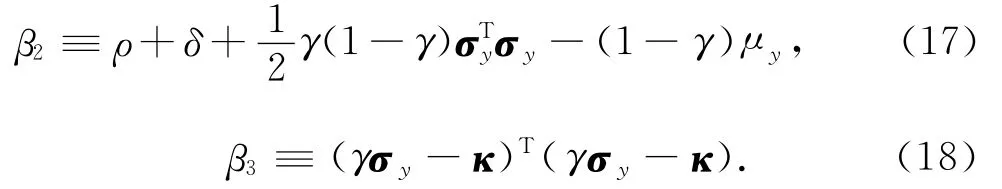
定理2 假定v>0,β1>0,β2>0,无需借贷和偿付约束在初始条件下有严格不等式
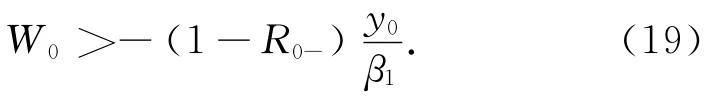
对于投资者问题Ⅱ,可以采用对偶变量xt来表示问题Ⅱ的解.对偶变量xt定义为
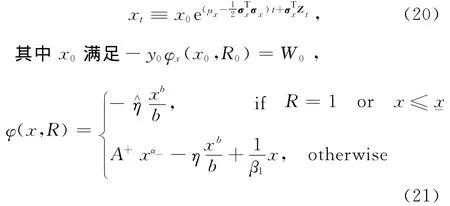
变量b,η以及η∧的定义见定理1,且
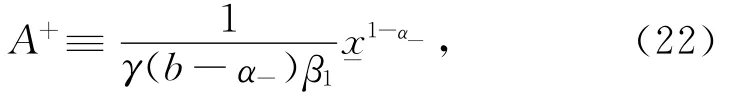
最优退休边界
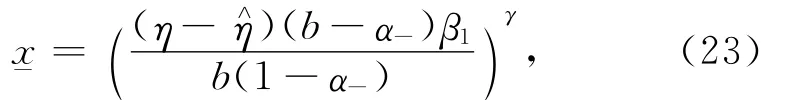
其中:
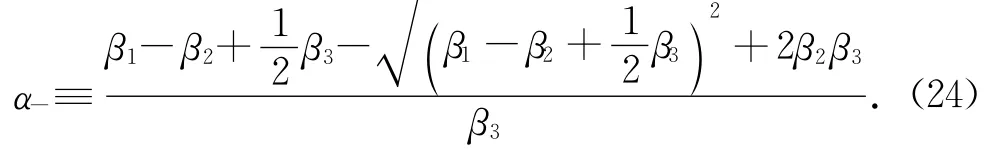
最优消费策略为
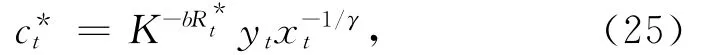
最优投资策略为
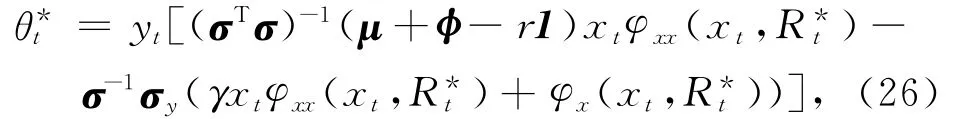
最优遗产策略为
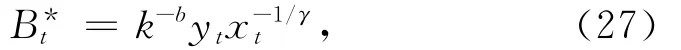
最优退休策略为
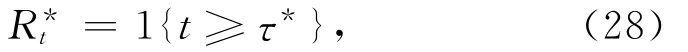
相应的退休财富门槛值为
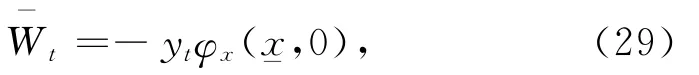
最优财富为
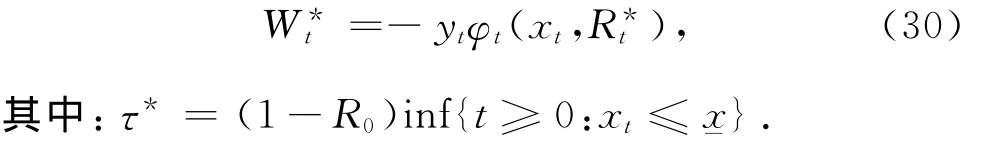
进而,其值函数为
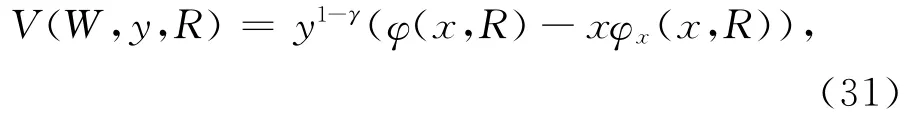
其中:x满足-yφx(x,R)=W.
定理3 假定v>0,β1>0,β2>0,W0>0.
投资者问题 Ⅲ的解与问题 Ⅱ的解是相似的,首先重新定义新的对偶变量xt
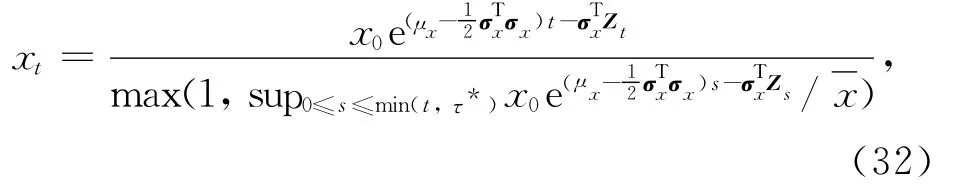
其中:x0满足 -y0φx(x0,R0)=W0,μx以及σx的定义见定理2,那么新的对偶价值函数为
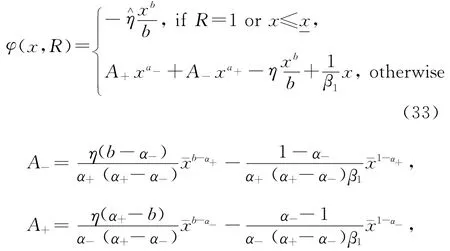
金融财富为0的x值为
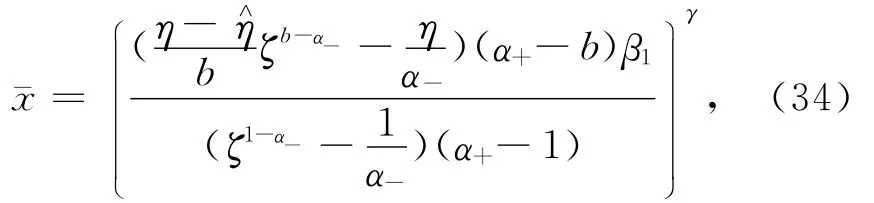
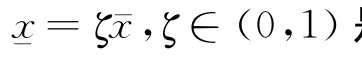
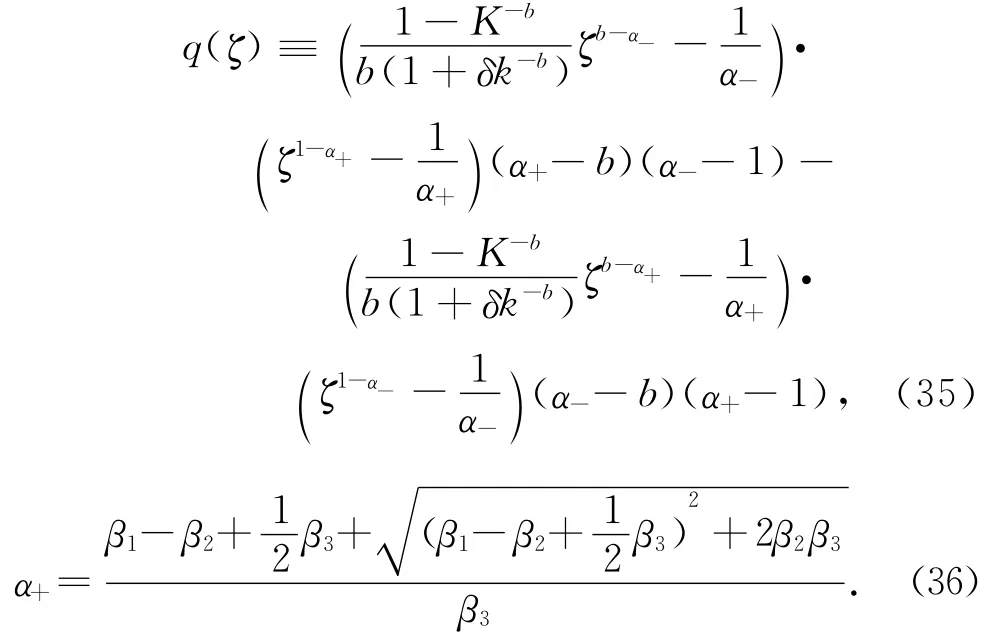
综合上述对偶变量xt和对偶值函数后,其他的解的形式同定理2中式(25)~(31).
定理2和3的证明与文献[4]中定理2和3的证明类似,故略.
考虑到定理1~3的最优策略,人力资本的市场价值在退休过后为0,在退休之前,定理1中,人力资本的市场价值为
H(yt,t)=g(t)yt,其中yt以及g(t)如前所定义.定理2中人力资本的市场价值为

其中yt,β1,xt,α-以及α+如前所定义.且
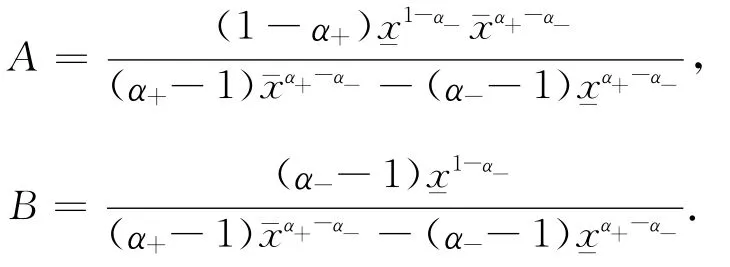
3 最优策略的数值分析
为了更好地说明消费与投资对财富的影响,进行数值分析.本文设参数值为d=1,μ=0.05,σ=0.22,r=0.01,φ=0.01,δ=0.025,ρ=0.01,γ=3,K=3,k=0.05,μy=0,σy=0和y0=1.
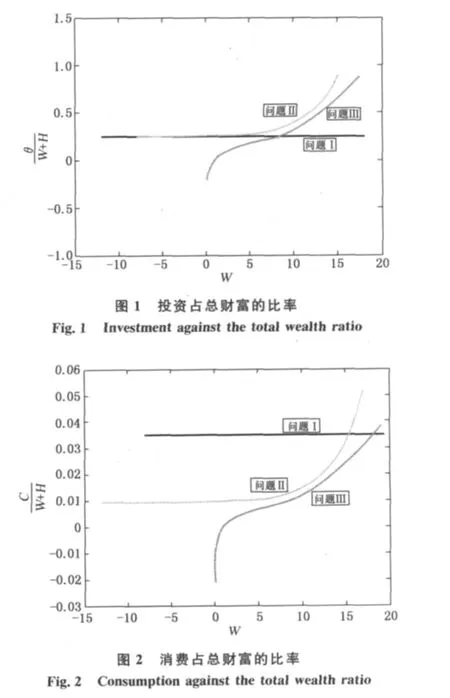
图1所示为3种情况中的投资(θ)占总财富的比率,其中总财富为金融财富W与人力资本H之和.从图1可以看出,如果未来所有的劳动收入都被资本化,那么问题Ⅰ情形下投资者在固定退休期20年间,在股票市场上的投资额占总财富的比率是恒定不变的.问题Ⅱ情形下,由于可以自由选择退休,导致了投资者投资在股票市场上的比例逐渐加大,这是由于投资者考虑可以自由退休,投资更多的资产到股票市场中以获得更多的财富,以达到提前退休的目的.问题 Ⅲ情形下,由于不能够对未来劳动收入进行借贷的约束,降低了初始的财富量,当财富水平在相对较低的水平下,投资在股票市场上的比率就要比问题Ⅱ的比率低得多,总体而言,问题Ⅲ情形下的投资比率要比问题Ⅱ情形下的投资比率要低.
图2所示为3种情形中的消费(C)占总财富的比率.从图2可以看出,问题Ⅰ情形下,投资者固定退休期为20年,可以对未来劳动收入进行借贷时,消费占总财富的比率是恒定的.问题Ⅱ情形下消费占总财富的比率表明灵活的退休策略,导致了随着财富逐步提高,消费占总财富的比率也相应地提高.这是由于财富量的增加,意味着提高了投资者对于即将退休,降低人力资本和退休后降低消费的预期.且在退休过后,投资者每单位消费的边际效用比退休前更高.问题Ⅲ情形下消费占总财富的比率表明在财富位于低水平时,消费明显偏低,导致投资者会将财富投入银行获得无风险的收益来抵抗市场可能出现的低迷.
同时,比较在投资股票市场上有无红利的情况下,投资比率与消费比率发生的变化.令参数值为d=1,μ=0.05,σ=0.22,r=0.01,δ=0.025,ρ=0.01,γ=3,K=3,k=0.05,μy=0,σy=0和y0=1.仅就问题Ⅱ情形下加以讨论,分别考虑φ=0.01和φ=0的情况.图3表示针对问题Ⅱ考虑股票无红利支付的情形,以及针对问题Ⅱ考虑股票支付红利的情形.由图3可知,在股票支付红利时,投资者的投资比率以及消费比率都比未支付的情况下要高.对于问题Ⅰ以及问题 Ⅲ的情况,与问题Ⅱ的情况相似.
4 结 语
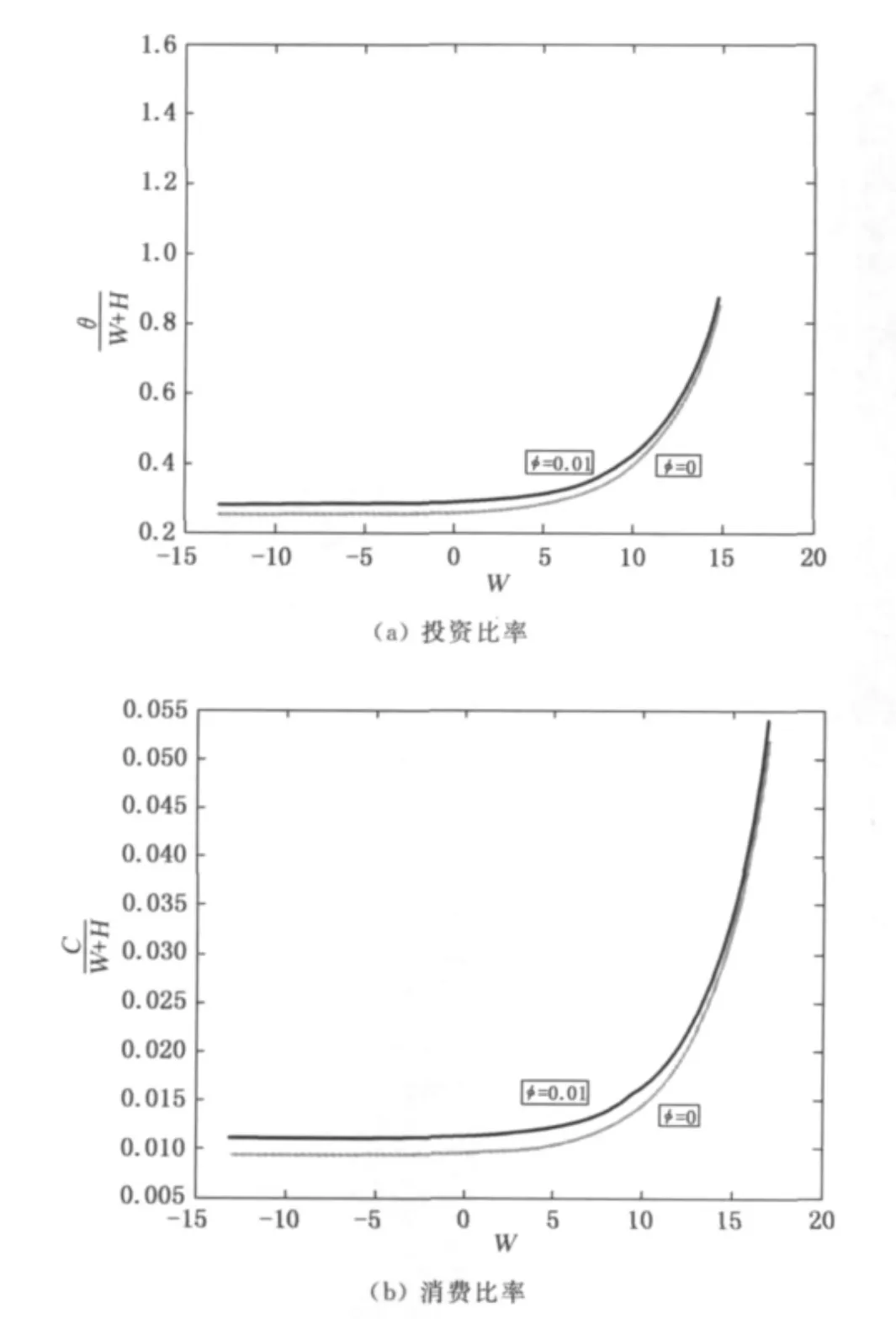
图3 股票支付红利的情形时的投资比率以及消费比率Fig.3 Investment and consumption ratios in the case of the stock dividend payments
本文在考虑红利分配、保险给付以及退休的情况下,研究了投资者的消费-投资和遗产行为.对文献[4]的现有模型进行了推广,并且借助随机微分方程理论以及鞅方法,解出投资者的最优消费-投资策略,并用数值分析分别说明了3种约束情形下投资占总财富比率以及消费占总财富比率对于财富的变化趋势,且考虑股票是否支付红利对投资比率以及财富比率的影响.通过对模型的扩展,使得结论更加符合经济实际.
参 考 文 献
[1]BODIE Z,MERTON R C,SAMUELSON W F.Labor supply flexibility and portfolio choice in a life cycle model[J].J Econ Dyn Control,1992,16(3/4):427-449.
[2]KWAK M,SHINB Y H,CHOI U J.Optimal portfolioconsumption and retirement decision under a preference change[J].J Math Anal Appl,2009,355(2):527-540.
[3]MUNK C.Portfolio and consumption choice with stochastic investment opportunities and habit formation in preferences[J].J Econ Dyn Control,2008,32(3):3560-3589.
[4]DYBVIG P H,LIU H.Lifetime consumption and investment:Retirement and constrained borrowing [J].J Econ Theory,2010,145(3):885-907.
[5]朱永王,费为银,苏凯.带有习惯形成的最优消费-投资与闲暇选择问题研究[J].南京信息工程大学学报,2012,4(5):476-480.
[6]衡传杰,郭文旌.CVaR限制下的动态最优投资组合策略[J].金融经济,2010,10(1):90-91.
[7]苏凯,费为银,朱永王.考虑红利支付与提前退休的最优投资组合研究[J].应用数学与计算数学学报,2011,26(1):77-84.
[8]KARATZAS I,SHREVE S E. Methods of mathematical finance[M].New York:Springer,1998.
Optimal Consumption-Portfolio and Bequest with Dividends and Retirement
FEIWei-yin,HEDan-dan,ZHUYong-wang,SUKai
(School of Mathematics and Physics,Anhui Polytechnic University,Wuhu Anhui 241000,China)
The problem of the optimal consumption and portfolio with the investor's heritage and insurance,in which the stocks have dicidend-paying under three different borrowing constraints,is studied.Firstly,the policies of the optimal consumption-portfolio and bequest of investors are explicitly provided by using of the stochastic differential equations and the martingale method.Secondly,through the numerical simulation,both the changes of the investment and consumption ratios are analyzed under the three different borrowing constraints.Finally,the effect of the dividends on investment and consumption is discussed.
dividends;optimal portfolio policies;voluntary retirement;stochastic differential equation;bequest
O 211.6;F 224.9
A
1671-0444(2013)01-0124-06
2011-12-12
国家自然科学基金资助项目(71171003,71271003);安徽省自然科学基金资助项目(090416225);安徽省高校自然科学基金资助项目(KJ2010A037)
费为银(1963—),男,安徽芜湖人,博士,教授,研究方向为金融工程.E-mail:wyfei@ahpu.edu.cn

