模糊线性回归方法在节假日短期负荷预测中的应用

瞿迪庆，陈红敏，吕理想

（永康市供电局，浙江 永康 321300）

模糊线性回归方法在节假日短期负荷预测中的应用

瞿迪庆，陈红敏，吕理想

（永康市供电局，浙江 永康 321300）

QU Di⁃qing，CHEN Hong⁃min，LV Li⁃xiang

（Yongkang Electric Power Supply Bureau,Yongkang 321300,China）

由于节假日负荷与正常日有较大差异，加之样本较少，节假日短期负荷预测一直是一个难点问题。为了降低节假日短期负荷预测的误差，创新性地引入了模糊线性回归方法对节假日短期负荷进行预测，结果表明，该算法预测精度较高，适用于节假日短期负荷预测。

相似日；线性回归；模糊模型；负荷预测

短期电力负荷预测是调度部门安排发电计划的重要依据。对于正常日，其负荷具有按工作日和休息日呈周期性变化的规律，数据相对较为充足，预测准确度一般较高。然而，对于国家法定节假日，如：元旦、劳动节、国庆节等，其负荷具有与正常日明显不同的变化规律。

一般要求提前对节假日多日负荷进行预测，预测样本数据缺少使得预测难度加大，节假日后，工厂企业逐步恢复生产，逐步增加的负荷也是负荷预测的难点。相似日线性回归法、模糊逻辑推理法、人工神经网络法、支持向量机法等被运用于节假日短期负荷预测，但都难以得到较为满意的预测效果，本文针对节假日负荷特点，创新性地引入模糊线性回归方法来提高节假日短期负荷预测的精度。

1 相似日线性回归分析法

相似日负荷预测表达式为

Y=ZZA+ξ（1）

式中：

Y

为预测负荷；Z

Z

为独立变量的矩阵；

A

为相似日负荷；

ξ

为随机误差。

式（1）亦可写成

y=a0+a1z1+…+akzk+ξ （2）

可以采取最小二乘法来求解未知参数A的估计量，作离差平方和

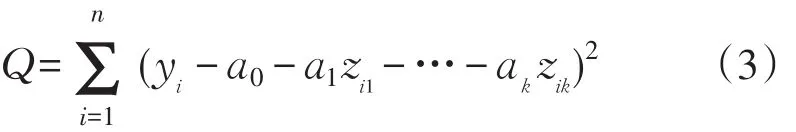
求解A，使得离差平方和Q达到最小。再将A代入式（1）中，从而求得负荷预测值。

2 模糊线性回归方法的模型

2.1 模糊数学的概念

模糊线性回归模型表述如下

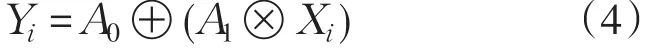
式中：Yi、Xi、A0、A1是模糊数字，⊕是模糊数字相加，⊗是模糊数字相乘。

一个三角模糊数字A被(a,α,β)定义如下

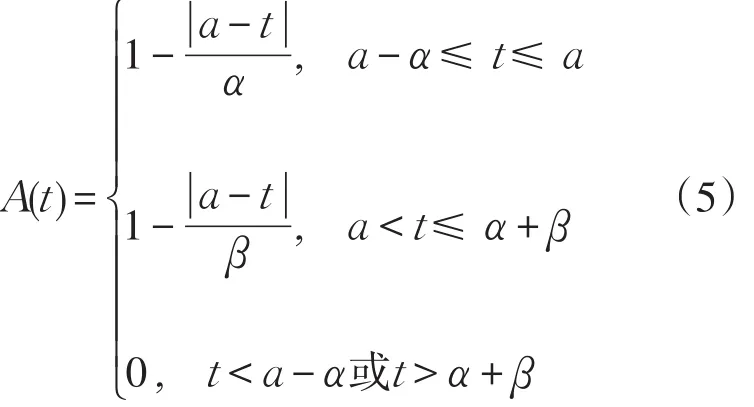
式中：a∈R是 A的中心，α＞0是左边的延伸，β＞0是右边的延伸，见图1。

如果α=β，那么三角模糊数字被叫作对称三角模糊数字，通过(a,α)方程式表示。

模糊数字的算术运算概括如下。

模糊数字加法⊕为

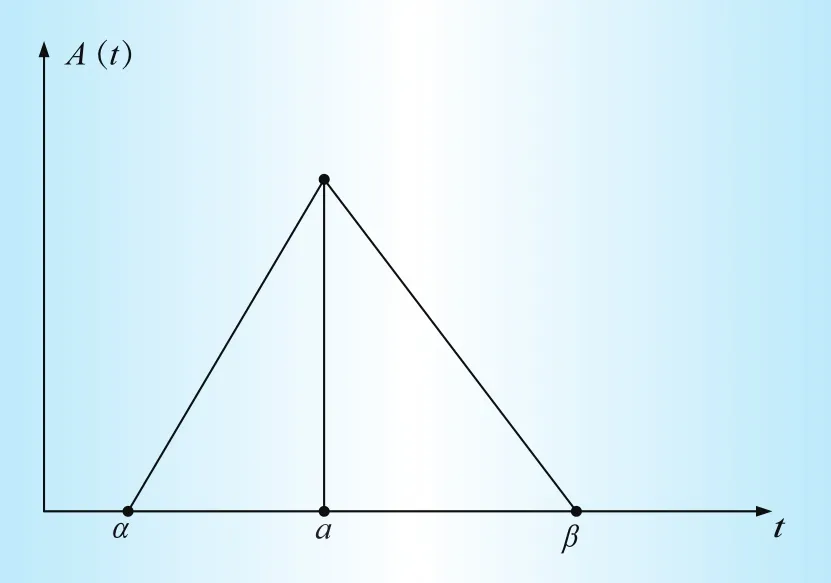
图1 一个模糊数字的图像

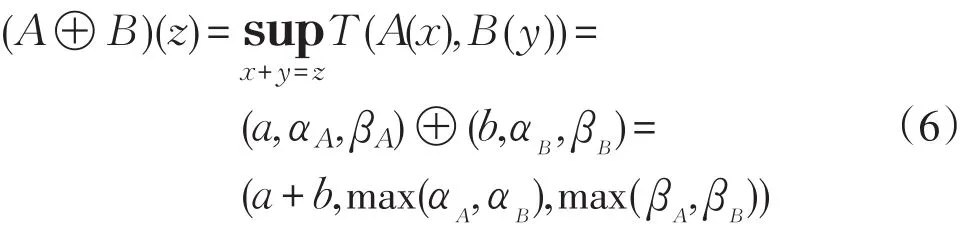
模糊数字乘法⊗为

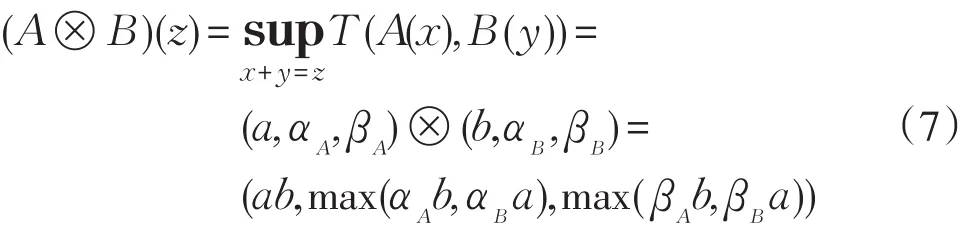
式中：A和B为模糊数字。

2.2 模糊线性回归方法模型的建立

模糊自变量Xi和模糊因变量Yi之间的模糊线性回归方程可用下式表示

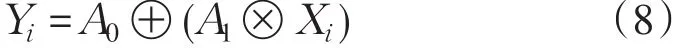
式中：Yi、Xi、A0、A1是模糊数字，A1为回归系数。

取模糊因变量Yi为对称三角模糊数字，Yi表示为Yi(yi,ei)，其中 yi为三角模糊数的中心值，ei为模糊幅度。取模糊回归系数A1为对称三角模糊数字，A1表示为 A1(a1,α1)，其中a1为三角模糊数的中心值，α1为模糊幅度。

式（8）根据模糊数字的算术运算法则，可得

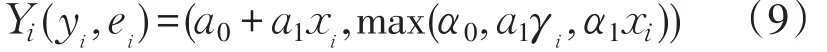
下面的问题是如何利用下列已知的m组观测数据(Yi,Xi，其中i=1,2,…,m)确定回归系数A1。首先要确定衡量拟合程度的指标，使得模型对已知数据的拟合最好。衡量拟合程度采用下式表示的贴近度

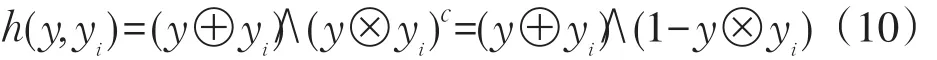
式中：y⊕yi= ∨(y∧ yi)为 y与 yi的内积，y⊗yi=∧(y∨ yi)为 y与 yi的外积，h(y,yi)为贴近度，贴近度h(y,yi)越大，表示 y与 yi越贴近。

为使模型对已知数据的拟合最好，根据式（10）目标函数可用如下形式表示

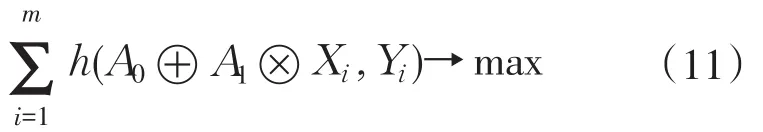
确定回归系数A1时，既要使模型对已知数据的拟合最好，还应使回归函数的模糊性尽可能小。式（11）中以贴近度的极值来确定A1比较困难，因此给定贴近度标准h0，将问题转化为在h(A0⊕A1⊗Xi,yi)≥ h0条件下使y的模糊度最小的规划问题，即

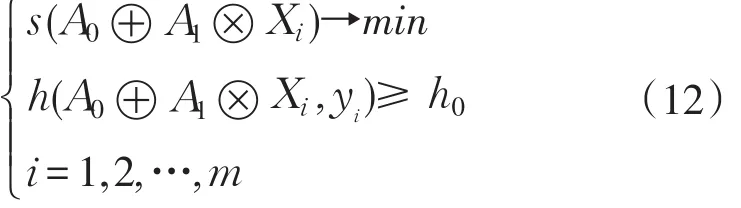
式中：h0为给定的贴近度标准，s(A0⊕A1⊗Xi)为 y的模糊度。

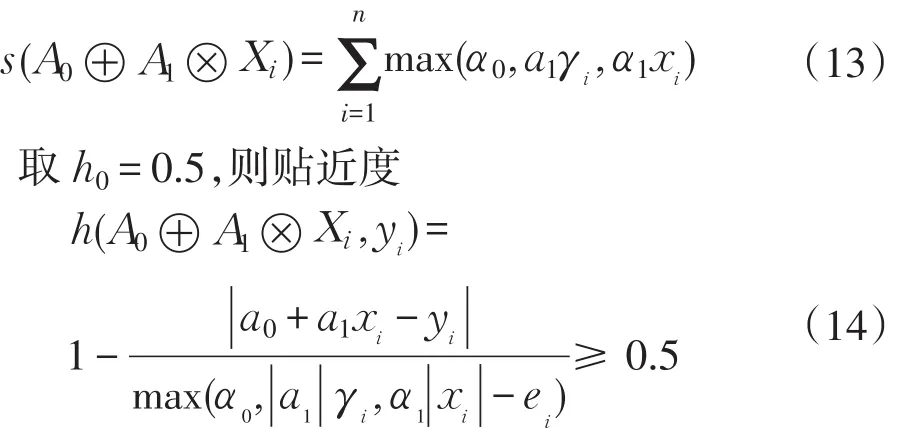
2.3 模糊线性回归方法应用

在 模 糊 线 性 回 归 的 模 型 中 ，A0∶(a0,α0)、A1∶(a1,α1)是对称三角模糊数字，这里 ai是 Ai的中心，αi是 Ai的延伸。 Xi和 Yi分别是 (xi,γi)和(yi,ei)，这里 xi,yi是平均值，γi,ei是标准背离。A0∶(a0,α0)和 A1∶(a1,α1)用 Xi∶(xi,γi)和 Yi∶(yi,ei)建立。在过去的i年中，对称三角模糊数字的样本Xi∶(xi,γi)，Yi∶(yi,ei)见表1。

表1 模糊输入数据

Xi∶(xi,γi)包含了在节假日前4天的每日高峰负荷的平均值和标准背离量。节假日前4天日高峰负荷的平均值为

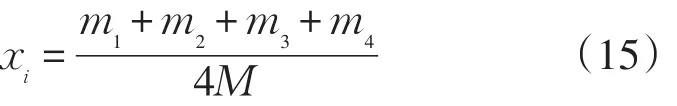
式中：m1、m2、m3、m4为节假日前4天的日最大负荷，M为 m1、m2、m3、m4中的最大值。

节假日前4天的每日高峰负荷的标准背离值为

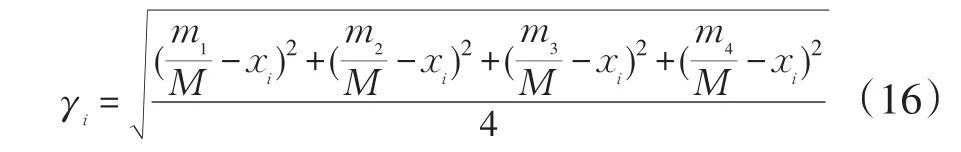
同理Yi∶(yi,ei)包含了节假日高峰负荷的平均值和标准背离值。

式中：m5为节假日高峰负荷值。

显然，Yi中的ei为0。对于过去3年的高峰负荷，在过去的3年中，对称三角模糊数字的样本Xi∶(xi,γi)，Yi∶(yi,ei)见表2。

表2 前3年的模糊输入数据

通过求解式（18）的混合线性规划问题，可以得到 A0∶(a0,α0)、A1∶(a1,α1)的最佳值。

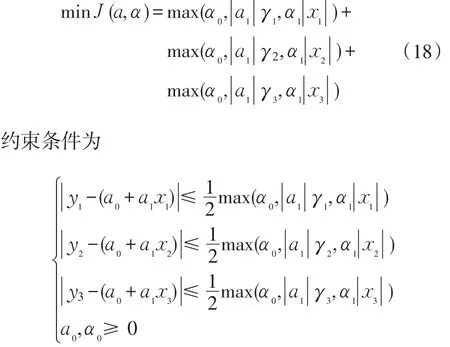
已知模糊输入数据X4，Y4可以通过（19）计算得到

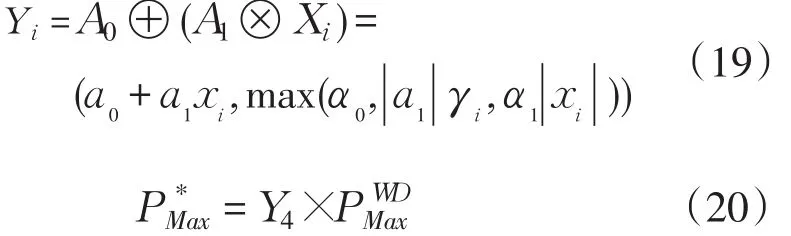
式中：是节假日预测最大负荷；Y4是估计的节假日规格值；是节假日前4天日最大负荷的最大值。

此算法同样可以预测出节假日最小负荷及24 h负荷。

3 算例分析

3.1 数据采集

本文样本为某地区2007—2010年的电力负荷数据，从中分别提取了4年中元旦节，劳动节，国庆节以及各节日前4天的最大负荷数据，其中前3年的数据以及第4年节假日前4天的数据作为输入，而第4年的节假日负荷数据作为实际值，用于和预测值之间进行比较，计算误差。

3.2 程序流程图

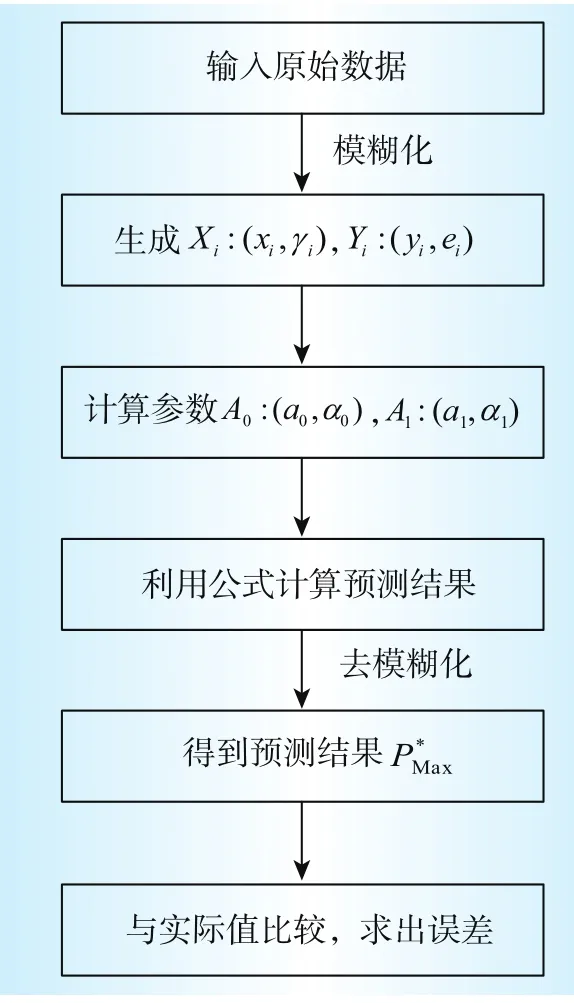
图2 模糊线性回归方法程序流程图

3.3 预测结果与分析

运用模糊线性回归方法预测的元旦、劳动节、国庆节最大负荷数据及误差如表3所列，平均误差为2.59%。

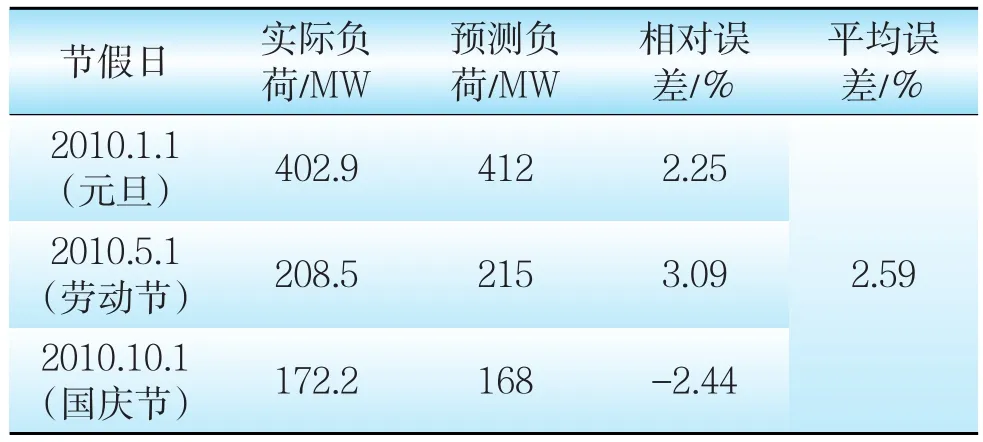
表3 节假日最大负荷数据及误差

将模糊线性回归法与相似日线性回归法、模糊逻辑推理法、BP神经网络法3种传统方法的计算结果进行对比，可以看出本方法误差最小，适用于节假日短期负荷预测。各种方法预测误差对比情况如表4所列。

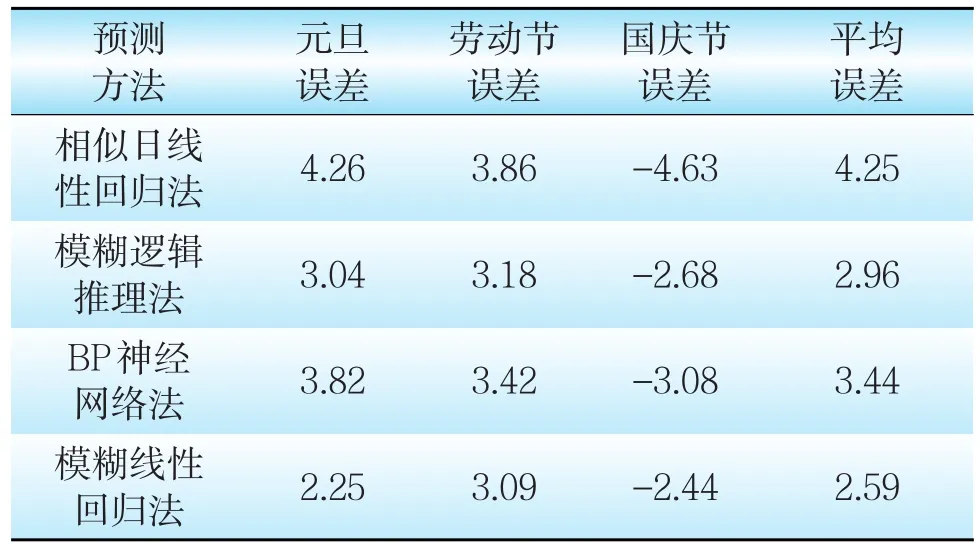
表4 各种方法预测误差%

同理，可以预测出元旦、劳动节、国庆节24点负荷数据，24点预测负荷和实际负荷比较曲线见图3。节假日24点负荷预测平均误差为2.75%。

图3 节假日24小时预测负荷和实际负荷比较图

4 结论

节假日短期负荷预测准确率一直是影响各地区负荷预测精度的一个重要因素。为了降低节假日短期负荷预测的误差，本文将模糊线性回归方法应用于节假日短期负荷预测，结果显示该算法预测节假日最大负荷平均误差为2.59%，节假日24点短期负荷平均误差为2.75%，与传统方法相比显示出明显优势。

：

[1]Kyung⁃Bin Song,Young⁃Sik Baek,Dug Hun Hong.Short⁃term load forecasting for the holidays using fuzzy linear regression method.IEEE Transactions on Power Systems,2005,20(1)：1 558-0 679.

[2]牛东晓.电力负荷预测技术及其应用[M].北京：中国电力出版社，1999.

[3]王平洋,胡兆光.模糊数学在电力系统中的应用[M].北京：中国电力出版社,1999.

[4]贺静,韦钢,熊玲玲.负荷预测线性回归分析法的模糊改进[J].华东电力,2003,31(11)：21-23.

[5]林辉,刘晶,郝志峰,等.基于相似日负荷修正的节假日短期负荷预测[J].电力系统保护与控制,2010,38(7)：47-51.

[6]所丽,丁恰,韩新阳.基于模糊推理的节假日负荷预测[J].中国电力,2009,42(11)：66-69.

Holidays short⁃term load forecasting using fuzzy linear regression method

Because the holidays load is quite different from the normal days and fewer samples,holidays short⁃term load fore⁃casting is always difficult.In order to reduce the error of the holi⁃days short⁃term load forecasting,this paper creatively introduces fuzzy linear regression method.The results show the algorithm has a high prediction accuracy and is suitable for the holidays short⁃term load forecasting.

similar day;linear regression analysis;fuzzy model;load forecasting

TM715；F407.61

A

1009-1831（2013）03-0016-04

2013-02-04；修回日期：2013-03-15

瞿迪庆（1986），男，浙江萧山人，助理工程师，本科，主要从事电网调度及继电保护整定计算工作；陈红敏（1976），女，浙江永康人，助理工程师，本科，主要从事电网调度及继电保护整定计算工作；吕理想（1983），男，浙江永康人，工程师，硕士，主要从事电网运行方式管理工作。

（

杜先波）