浅析数学课程教学方法和评价的改革——以《微分几何》课程为例

张先叶

(渭南师范学院数学与信息科学学院，陕西渭南714000)

高等师范院校的首要任务是培养合格的中学教师．面对要求越来越高的的中学教育，师范院校也在课程内容、学习方式、教学方式、学校的教学管理与评价方式等方面做出相应的改革［1－5］．笔者在《微分几何》的教学中，反思传统的课堂教学模式和评价方式，进行教学方式的多样化设置，采取引导探究、小组讨论、研究性学习等学习方式，并在微分几何的教学中开展数学实验;从评价内容和评价主客体的多样化入手，使评价方式更科学合理．经过多年的探索与实践，获得了一定的经验与体会，以下就从教学方法和教学评价两方面的改革进行介绍．

1 教学方法的改革

教师的教学方法与学生的学习方法相互影响，教师的教法可以转化为学生的学习方法．师范生在校的学习方式可以转化为他未来的教学方式［2］．经历“大学教法——学法——中学教法”的转化过程，实现从学生向教师角色的转变［3］．因此，为使高师生适应基础教育新数学课程的教学，高师数学教育必须改变教学方式．

1．1 课堂教学模式:讲授型→讲授型与研究型相结合

微分几何课程是解析几何、数学分析、高等代数、微分方程等几门专业课知识的综合应用．综合性和抽象性都是比较高的．因此首先结合课程特点，研究课程内容，认真分析哪些适合研究，哪些适合讲授，二者如何有机结合，然后再根据自己的教学风格，确定具体的教学方法，在课堂教学中进行改革探索，再根据学生实际情况的反馈，进一步修改，同时整理收集改革成功的章节．例如“向量函数的概念”［6］这一节，包括向量函数的概念、极限、连续性、微商、泰勒公式及积分，教材的编排以及传统的讲授，均由《数学分析》的有关内容类比得到相关结论，再利用数学分析的方法，借助向量工具来证明．那么，在设计教学方案时，采用对向量函数的概念和极限进行讲授，其他的都是学生自己研究．

1．2 学生学习模式:听练学习型→听练型与讨论研究型相结合

课前预习、课中听讲练习、课后做习题巩固知识，是传统的数学课程学习模式．我的改革主要在拓展课前、课中、课后的作业形式和学习方式．课前:结合教学内容布置相应的思考题;课后:布置拓展作业;课中:提供听练机会，创造讨论研究的条件，以此开阔学生的思维，改变学生学习数学的传统模式．例如“空间曲线的基本三棱形”［6］是曲线论的核心内容，既是曲线论的重点，又是难点．我们课前给学生预习的思考问题:(1)什么是曲线的三个基本向量，用什么符号表示?(2)三个基本向量间的关系怎样?(3)曲线上不同点的Frenet标架有什么关系?(4)三个基本向量所在直线叫什么名称，方程怎样?(5)其中任两条直线所确定的平面叫什么名称，方程怎样?(6)如果曲线方程)，该曲线的三个基本向量如何得到?在课堂上，就围绕这6个问题进行．问题(1)、(2)、(4)和(5)都属于听练相结合的学习模式，而(3)、(6)就要讨论研究．并对此要求学生课后参考学习整体微分几何活动标架的部分内容．

1．3 教学授课模式:传统与现代教学技术相结合——开展数学实验

近年来，数学软件的开发和计算机技术的发展使数学学习也可以由教室走进实验室，数学实验使得数学学习方式由纸笔进行研究转化为一种借助计算机，以数学理论为基础，以数学软件为平台的研究性学习方式［1］．目前流行的用于数学实验的常用工具:Maple、Mathematica、Matlab，利用这些数学软件提供的函数可以解决大量的数学问题，对于微分几何中的一些抽象的图形．可以在实验中展现图形的生成过程，绘制各种复杂曲线、曲面，对三维图形进行空间旋转，多角度展示图形的结构，演示图形与图形之间的变换关系以及曲线生成曲面的动态过程，这样能够优化数学知识的呈现形式，提高数学课堂教学的质量和效率．例如在学到切可展曲面时，为了使学生能更好地认识这种曲面，我们利用Matlab画出螺旋线它的切可展曲面

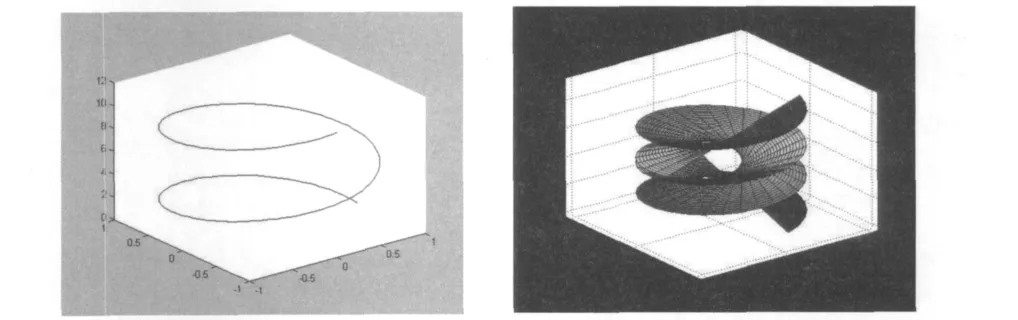
在《微分几何》的教学中引入数学实验，能够更加易于理解和接受教材中的概念，快速地验证教材中的结论，准确地进行相关的代数运算，更主要的是克服了讲解内容抽象、手工绘图不准确等不足，提高学生的学习兴趣，更深入地掌握本课程的内容，也培养了学生利用计算机解决实际问题的能力．当然这一点要求教师除了要有扎实的数学知识外，还要熟练掌握数学软件的基本功能，合理设计数学实验内容，以数学实验为桥梁来提高学生的数学应用能力．

2 教学评价改革

评价是促成教学目标实现的重要手段之一，对教学效果的评价方式直接影响着教学改革的方向和成败，关系到高校既定人才培养目标，所以研究高等教育教学效果评价具有重要意义［5］．评价的目的是为了促进师生的共同发展．长期的、单一的以考核知识为目的考试，对学生的能力和素质的多元发展有着抑制作用．我们主要从评价内容和评价主客体的多样化进行探索．

2．1 评价教学结果改革为对结果和过程的双重评价

随着微分几何课堂教学改革地深入，课堂教学就会实施多种教学模式，例如引导探究、小组讨论、研究性学习等，只注重结果的传统的单向评价来考核教学效果，已经无法检验改革的成败，因此，继课堂教学改革之后，也探索评价方式的改革，一起协商、制定新的评价方案，对教学结果和教学过程进行双重评价．教学过程中的课中表现、课前预习与课后扩展均纳入考核内容，基本确定其在综合成绩中的比例(占20%～30%)，对知识技能掌握评价，为学会学习评价以及研究能力形成的评价．例如，通过学生课堂表现看学生课前准备的情况，通过对前一节的复习、课后思考题的考察，评价学生课堂和课后习得情况．

2．2 改革评价主体一元化为评价主体的多元化、互动化

一直以来我们以单一的教师为评价主体来评价学生，学生作为评价对象被排除在评价主体之外．但是数学学习是一个合作的过程，班级内的同学也有发言权，可以让学生开展自评和互评，学生的互评也是至关重要的．我们不能忽视学生的自主评价，让老师、学生都参与到评价中，使评价成为多主体共同参与和协商的活动．多主体评价能够从不同的角度为教师提供有关学生学习、发展状况的信息，有助于学生更全面地认识自我．

2．3 改革评价对象一元化为评价对象多元化

评价对象除了学生在知识体系、学习态度、创新意识和实践能力等方面外，还要评价教师的教学水平、教学态度等等．我校已经实行学生网上评价任课教师，这就是对教师教学水平的评价．教学效果不仅体现在学生的成绩上，还体现在学生情感的发展上．通过分析各种能够反映教学效果的因素，如师生对教学过程的满意度、课堂上师生的和谐程度、教学目标完成的情况等;对教学的各个阶段进行评价，评价主体将包括学生、教师、试题、考试方法等，教师教学效果由学生和同行专家评价;学生学习水平与方法由教师和学生共同评价;试题质量及考试形式由教师和专家共同评价．由此可以看出，评价主客体的交互性、多元化．经过几届学生的检验:学生的学习状态、课堂参与程度和教师教学中存在的问题，都可以在评价结果中反馈出来，使教师能够对照反馈结果进一步改进教学方法，调整教学策略，教师的教学效率和学生的学习水平得到提高．

以上是就微分几何这门课程多年的教改总结．在教改实践中，也深感教学改革所受到的制约因素太多，需要教师、学生、职能部门的协调配合．例如专业课时的数量、数学实验的安排等等，这些还需要不断改进，以期教学活动达到更好的效果．

［1］曹一鸣．数学实验教学模式探究［J］．课程·教材·教法，2003，(1):46－48．

［2］杜玲玲．数学教育专业学生培养中的若干因素及关联分析［J］．数学教育学报，2002，11(3):69－71．

［3］孔凡哲．高师数学教学方法的现状及改革尝试［J］．数学教育学报，1998，(7):71－74．

［4］黄青群，罗日才．Matlab在微分几何教学中的应用研究［J］．河池学院学报，2009，(8):96－99．

［5］牛惠芳，王淑玉．教学效果评价方法研究［J］．数学教育学报，2010，19(4):89－91．

［6］梅向明，黄敬之．微分几何［M］．第4版．北京:高等教育出版社，2009．

［7］［美］John Oprea．微分几何及其应用［M］．陈智奇，李君，译．北京:机械工业出版社，2006．