6R工业机器人运动学算法的改进*

吴 挺，吴国魁，吴海彬

(福州大学机械工程及自动化学院，福建福州350108)

0 引 言

机器人运动学在机器人运动控制中扮演着重要角色。机器人特别是工业机器人主要用于完成一定的作业任务，在完成任务过程中不可避免地要进行关节坐标空间与笛卡尔等坐标空间的相互转换，不可避免地要进行正运动学、逆运动学的求解以及插补算法等运动学方法的实现。机器人运动学的作用不言而喻。

机器人运动学涵盖面较广，本研究只研究其中较为重要的运动学逆解及其优化选取、插补算法及一些常用坐标系的建立方式。目前，运动学逆解的方法主要有数值迭代法［1］、几何法［2-3］，神经网络法［4］及遗传算法［5］等方法。机器人运动学逆解算法复杂，数值迭代法依赖于初始点，收敛速度较慢。几何法依赖于机器人的机构模型。遗传算法涉及大量个体的计算，难以满足控制系统实时性的要求。在对逆解的选取时有学者提出一种基于“最短行程”的方法［6］，但该方法忽略了机械手当前状态，且需要求出机器人的所有解，实时性不高。在插补算法方面也有不少学者提出一些插补算法［7］，但一般只介绍位置插补的实现，对于姿态插补却没有给出明确的算法。

本研究采用分离变量法求取逆解，提出一种基于机器人几何结构及解的特点的逆解优化方法，该方法无需求出机器人的所有逆解便可选择出较好的逆解，可节约机时，提高实时性，在插补算法中同时综合位置与姿态插补，以满足轨迹规划中对位置和姿态的要求。

1 工业机器人运动学逆解的求法

1.1 逆解求解过程

本研究研究的6自由度工业机器人如图1所示，根据D-H法［8］对机器人建立坐标系。为了计算方便，这里在机器人末端三轴交汇处建立了坐标系z6－x6，并在执行器末端建立了与z6－x6固连的坐标系z7－x7。因此，坐标系7并非按照D-H法建立。机器人DH法关节连杆参数表，如表1所示。

图1 机器人D-H表示法参考坐标

表1 机器人D-H参数表

依照D-H表示法原理，可得出相邻坐标系间的变化矩阵，记为:A1、A2、A3、A4、A5、A6。6 个变换矩阵可按下式计算:

由于执行器形状的不同，坐标系7的姿态和位置也会不同。但对于一定执行器，坐标系6和坐标系7的→关系是固定的。坐标系7可由坐标系6经过平移变换，再依次绕自身坐标系的 x，y，z轴旋转3个角度φx，φy，φz得到，这些参数可以由执行器的几何结构得到。故变换矩阵A7可表示为:

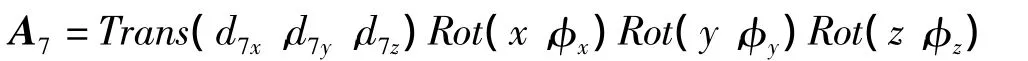
给定末端位姿矩阵T:

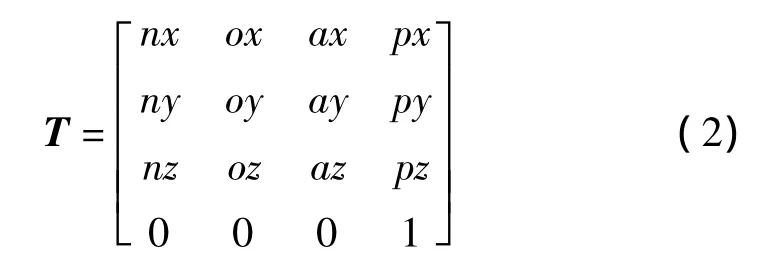
解方程T=A1A2A3A4A5A6A7的过程即为求逆解过程。注意到 A7为常量矩阵，可在方程 T=A1A2A3A4A5A6A7两边同时右乘A7的逆矩阵，得到:

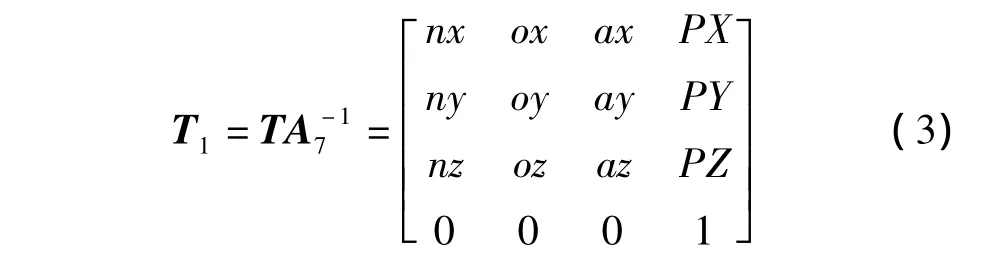
式(3)中的参数均由TA7－1计算得来，这里为了书写方便，将其各用一个参数替代。对A7处理后，相当于将图1中执行器末端坐标系原点等效到了机器人末端三轴交汇处。于是逆解的过程也转化为求T1=A1A2A3A4A5A6的过程，不必再考虑坐标系z7－x7。

易知手腕3个转动关节轴线交于一点，满足Pieper给出的具有封闭解的条件［9］，故可用如下方法求逆解。由于运动方程中有许多角度的耦合，研究者不能从矩阵中提取足够的元素来求解单个的正弦和余弦来计算角度。为使角度解耦，可以用矩阵T1左乘矩阵An－1，进行变量分离，再对比左右矩阵求得相应角度。

可得如下方程:

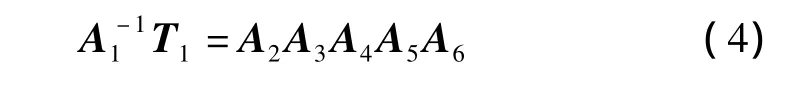
比较方程左右两边，由两边矩阵中元素(3，4)相等得到:

考虑式(4)左右两边矩阵中元素(1，4)和(2，4)相等，并计算化简可得:

考虑式A2－1A1－1T1=A3A4A5A6左、右两边矩阵元素(1，4)和(2，4)相等，可得:

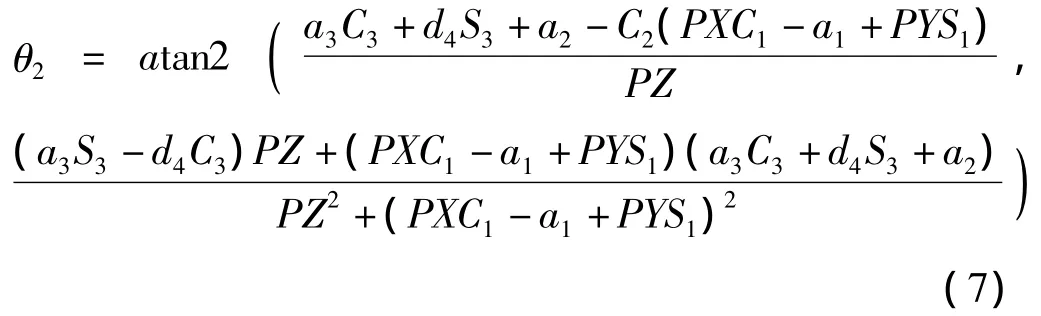
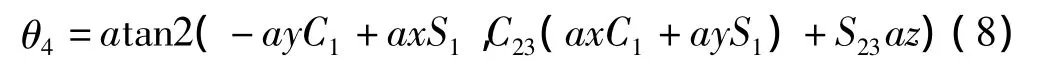
或者:

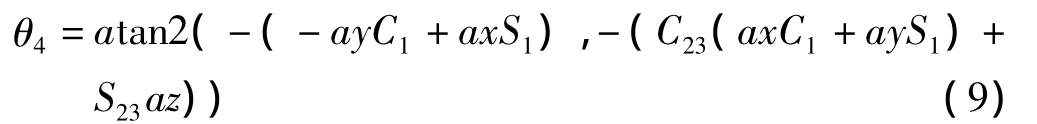
考虑式 A4－1A3－1A2－1A1－1T1=A5A6左右两边矩阵中元素(3，1)和(3，2)相等可得:

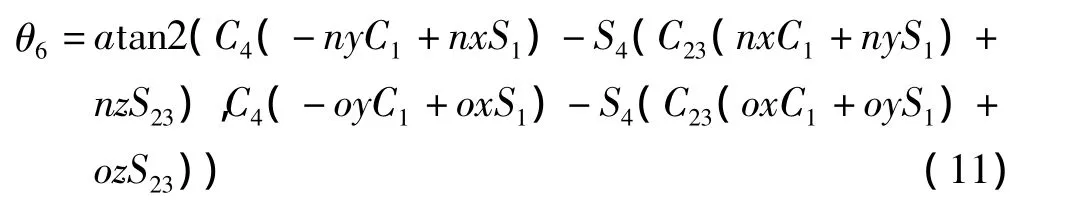
1.2 逆解优化选取

从以上求取逆解的过程可以看出，对应于某一位置，可以有8组不同的封闭解。但实际的机器人运动控制只能选择其中一组解，并且关节角转角是有范围限制的，同时，在轨迹运动时，如何使各关节变化平缓，减少机器人工作过程中角度突变，也对解的选择提出了要求。

在进行轨迹跟踪时，为了减小关节运动的时间，使各关节变化平稳，应使目标关节角与当前关节角尽可能接近。可以采用下式来选取逆解:

式中:θigoal—第i关节角的目标关节角，θinow—第i关节角的当前角度。

选取关节角度时，所要的关节角应满足使K值最小。但该法需要算出机器人的所有封闭解，从中选择出使K值为最小的解，这样会浪费机时去求无用解，且算法较为复杂，效率不高。

可以从机器人结构及解的特性来简化算法。在运动中为使机器人有较好的轨迹跟踪精度，则必然要求每次转过的关节角较小。从上文求出的θ1来看，θ1对应的两个解相差180°，从中可以得到一个与当前θ1较接近的解，另一个解可以直接舍弃。选定了θ1后，θ3只有两个解且θ3的两个解相差的角度依赖于θ3的大小，θ2完全依赖于θ3和θ1，因此可以求出这两组解，采用下式来选取使J最小的解:

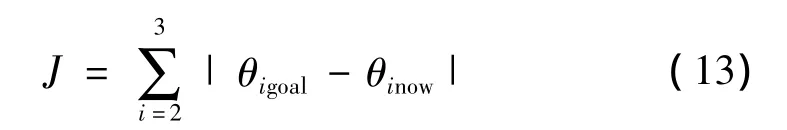
θ4的两个解也相差180°，选择与当前角度相差较小的解，否则从图1中工业机器人的结构可以看出后面的两个关节角将产生突变，这是不允许的。θ5和θ6完全取决于前面的解。至此，已选出一组较好的解。该法可以避免去解不符合要求的解，提高效率，简化算法。具体流程如图2所示。

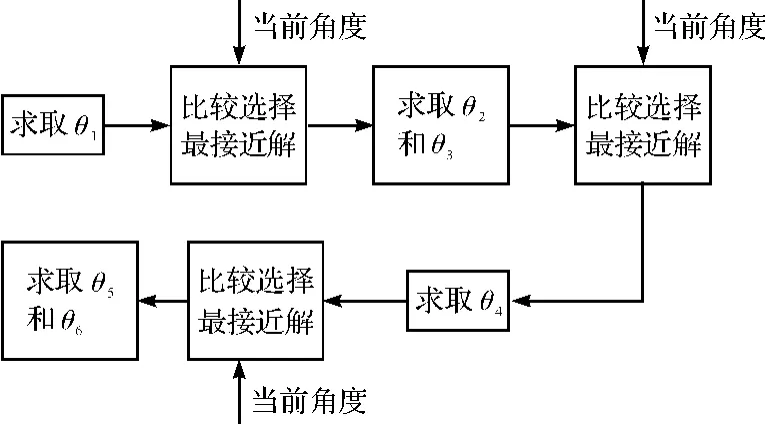
图2 逆解选取流程

2 插补算法

轨迹规划在机器人运动控制中具有重要的作用，对机器人的作业有着重要的影响。本研究所述轨迹规划是在笛卡尔坐标系下进行的，必须运用插补算法并反复求解逆运动学方程来计算关节角。插补算法在轨迹规划中具有重要的地位，因此研究它具有重要的意义。在笛卡尔坐标空间中描述机器人末端执行器，包括位置描述和姿态描述，因此需要对位置进行插补，同时也要对姿态进行插补。

总体原则是:在进行插补时，将起点和终点间的变换分解为一个平移(位置插补)和一个绕空间中某根轴k的旋转(姿态插补)。平移实现末端执行器坐标系原点的移动，旋转实现末端执行器姿态的改变，两变换同时进行。

2.1 位置插补算法

空间曲线的位置插补可以近似地等效为由直线段和圆弧段所组成，对应的位置插补就是直线插补和圆弧插补。

对直线插补，设直线的起点坐标为A(XA，YA，ZA)，终点坐标为B(XB，YB，ZB)，选定插补次数N，则有:

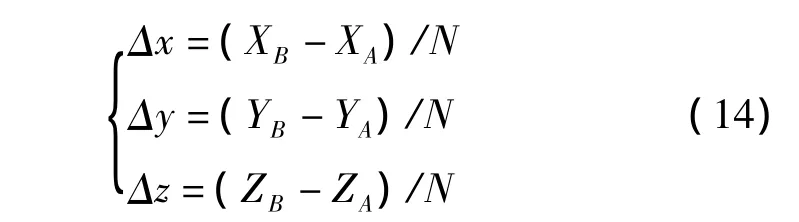
于是直线的插补点(xi，yi，zi)可以表示为:

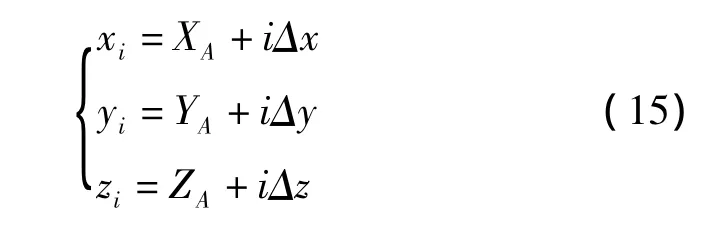
其中:0≤i≤N。

对圆弧插补，设该圆弧为由空间中任意不共线的3点A、B、C所组成的，示意图如图3所示。

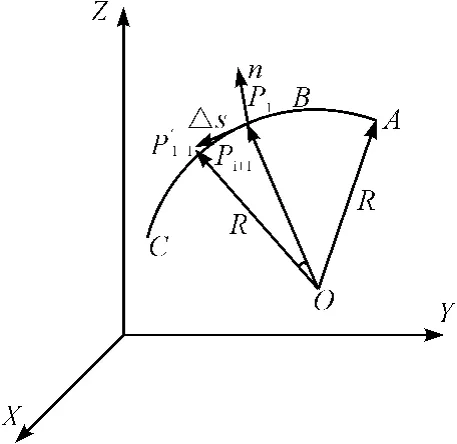
图3 圆弧插补示意图

易得线段AB的中垂面、线段BC的中垂面如下:

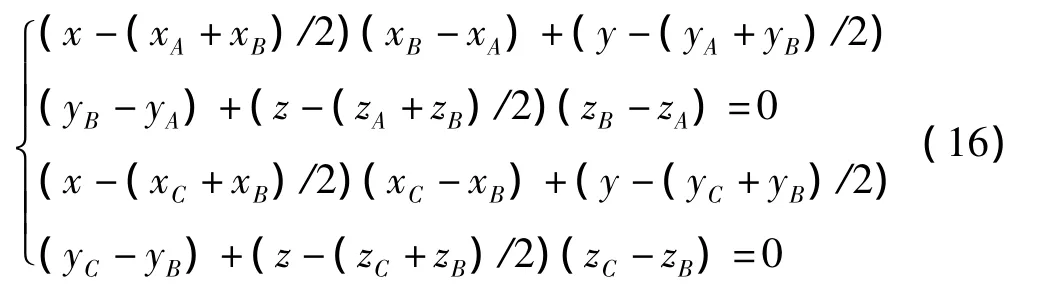
以及点ABC所在平面的方程如下:

联立以上3个方程，解方程便可得到圆弧的圆心坐标(x0，y0，z0)，进而可得到圆弧半径R和圆心角θ。给定插补次数N，则可得步距角δ=θ/N。为求插补点坐标可按图3所示过Pi点做切线PiP'i+1，进而得到圆弧上的点Pi+1，该递推公式已有学者推出［6］。

2.2 姿态插补算法

根据曲线特点可将姿态插补分为有中间点约束的姿态插补(如圆弧插补)和无中间点约束的姿态插补(如直线插补)。

对无中间点约束的插补，设起点到终点的姿态转换矩阵为T，并将T扩充为一个齐次矩阵R。设R为:

则可将该旋转变换(矩阵R)转化为绕空间中某个k轴旋转θ角得到，得到的k轴单位向量(u1，u2，u3)和转角 θ可表示如下［10］:

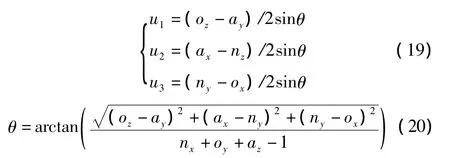
此外，可以得到绕k轴转过某个角度θ1得到的转化矩阵T(θ1):

于是姿态的插补便可转化为转角θ的插补，插补次数为N，则有:

插补点的姿态可以表示为:

式中:0≤i≤N，TA—直线初始点的姿态。

将插补点的位置与姿态结合起来，便可得到插补点的位姿矩阵，再利用逆运动学方程便可解出各个关节角。

对有中间点约束的姿态插补，如图3中的圆弧插补，考虑中间点B的姿态，可按下述方法进行。由下式可得AB弧所对圆心角θAB:

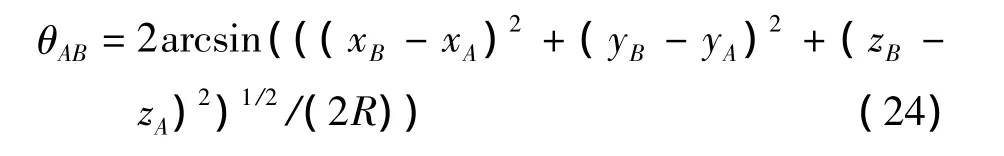
对NAB=NθAB/θ取整，可得AB弧的插补次数NAB，BC弧插补次数NBC=N－NAB。由此便可分别对AB弧和BC弧进行姿态插补，方法同直线插补。

2.3 位置和姿态插补综合

轨迹插补需要有位置和姿态信息才能进行，需要将插补点的位置与姿态结合起来，得到插补点的位姿矩阵，再用逆运动学方程便可解出各个关节角。由上文可以得到插补点的位置Pi(xi，yi，zi)T，及姿态矩阵Ti，由此便可得到插补点的位姿矩阵Ri:

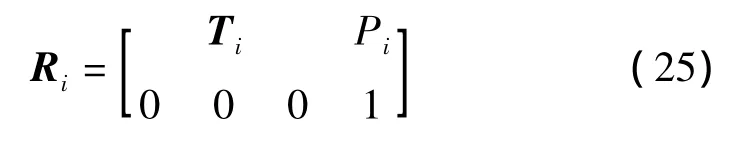
3 不同位姿表达方式之间的转换

工业机器人的运动学控制，位姿状态的表述通常采用位姿矩阵，但是位姿矩阵中姿态参数较多且不相互独立，在做速度或力矩控制时，往往由于雅克比矩阵无法从位姿矩阵直接通过计算得到而带来麻烦。而如果采用相互独立的6参数表示机器人末端执行器的位姿状态，并建立该6参数分别与6个关节角之间的函数关系式，则可以较方便地得到雅克比矩阵。这6个参数分别是:dx，dy，dz表示执行器坐标系原点坐标，3个角度 φ1，φ2，φ3分别表示绕参考坐标系的 x，y，z轴转过的角度。它可以较为形象地表达机器人的位姿。

3.1 由旋转参数转化为位姿矩阵

记Rot(d，θ)表示为绕d轴旋转θ角得到的位姿矩阵。则按顺序依次绕参考坐标系x，y，z轴旋转后所得的的矩阵R可按下式计算:

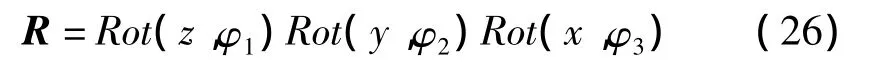
3个位置参数可以看成，旋转后再相对于参考坐标系平移(dx，dy，dz)，于是最终的位姿可按下式计算:

3.2 由位姿矩阵转化为旋转参数

设机器人位姿矩阵为T:

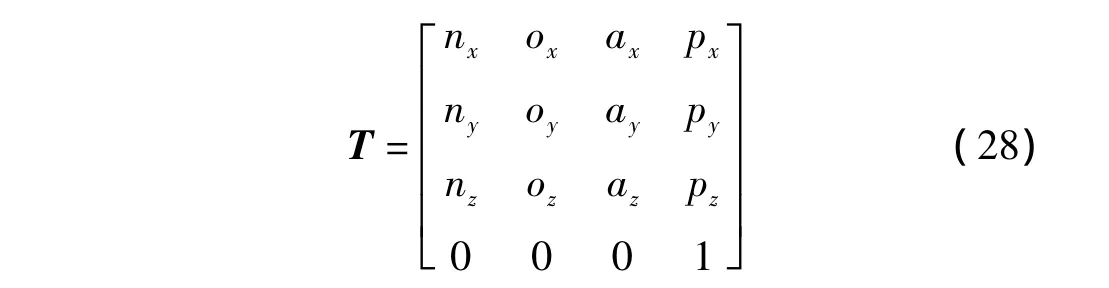
则有T=R，比较矩阵两边元素，可得:

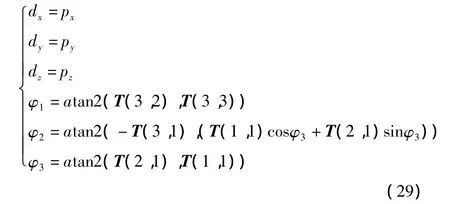
式中:T(a，b)—矩阵T中第a行第b列元素。

此外，矩阵T可由机器人正运动学得到，设6个关节角分别为 θ1，θ2，θ3，θ4，θ5，θ6，则矩阵 T 中元素均可表示为 θ1，θ2，θ3，θ4，θ5，θ6的函数。将其代入式(25)中，可得:

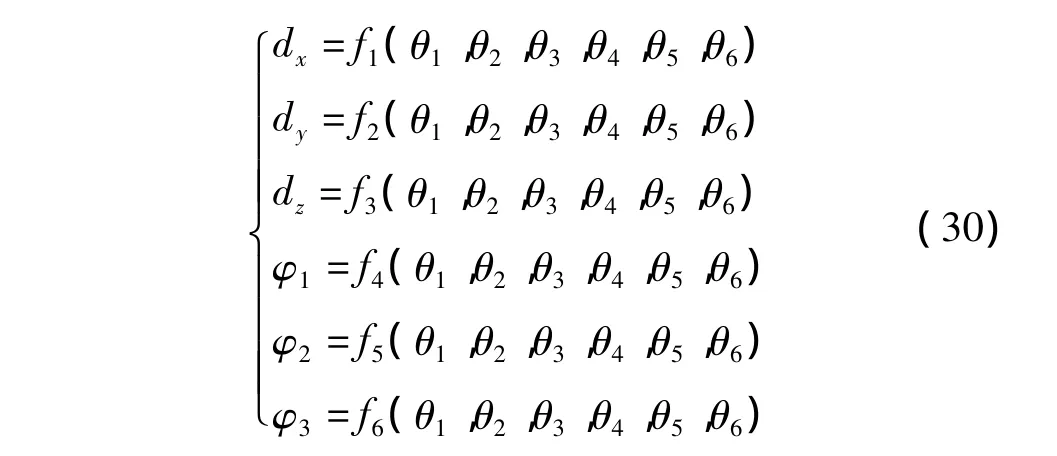
对式(26)求微分，则可直接得到雅克比矩阵，并可用于机器人的速度控制。

4 用户坐标系的建立

对用户来说，工业机器人参考坐标系的建法未必很明确和实用，参考坐标系往往不方便于空间定位，且随着环境改变，描述操作对象的坐标系也应随之而变。为了能够方便地操作机器人，更好地实现工作空间中的定位，更好地规划机械手的运动，有必要找到一个能够建立坐标系并实现其与机器人参考坐标系相互转化的方法。

为了建立这样一个坐标系，用户需要给定3个适当的点，设为A，B，C，其中点A为用户要建立的坐标系原点，B为用户建立的坐标系x轴正向上一点，C为用户建立坐标系的xy平面中的一点。用户坐标系的建立如图4所示。

图4 用户坐标系的建立

得到用户坐标系后，就可以比较方便地确定空间中的点在该坐标系下的坐标。为了让机器人识别这些点，需要研究用户坐标系与机器人参考坐标系的相互转化。设用户坐标系为U，机器人参考坐标系为S，用符号STU表示坐标系U相对于坐标系S的转化矩阵。已知用户坐标系下的点UP，可由式转化为机器人参考坐标系下的点的坐标。同理由UP=可将机器人参考坐标系下的点转化为用户坐标系下。若已知用户坐标系下的位姿矩阵UTR，可由式得到其在机器人参考坐标系下的位姿矩阵。由式可将机器人参考系下的位姿转化为用户坐标系下的位姿。

5 实 验

实验借助一台工作半径为650 mm的垂直6关节工业机械手，将以上算法编成动态链接库，通过VC++程序调用动态链接库来控制机械手的运动。在机械手做直线插补过程中，采集空间位置坐标和6个关节速度，并与原出厂程序控制的机械手的位置和速度进行对比。采集得到的位置坐标如图5所示。本研究算法得出的轨迹如图5(a)所示，机械手的出厂程序得出的轨迹如图5(b)所示。

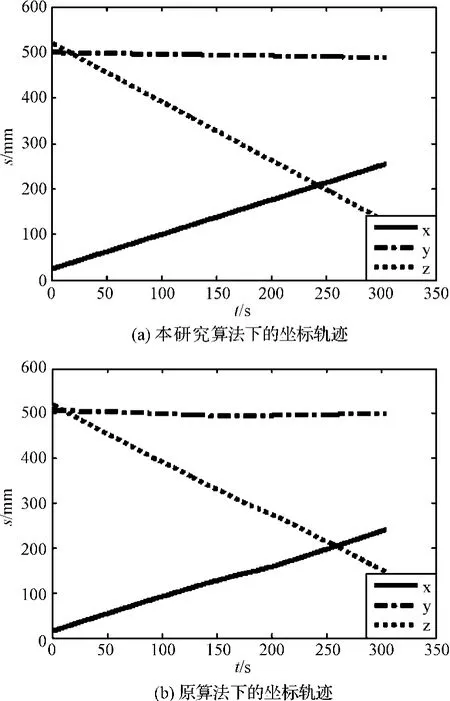
图5 空间坐标轨迹对比图

从图5可以看出，图5(a)的直线跟踪能力比图5(b)强。由此可得，改进后的逆运动学和插补算法是可行的，并且比原算法具有更强的直线轨迹跟踪能力。

机械手在做直线插补时前4个关节的速度曲线图如图6所示，采用本研究提出的方法得到的曲线如图6(a)所示，采用原出厂程序得到的曲线如图6(b)所示。

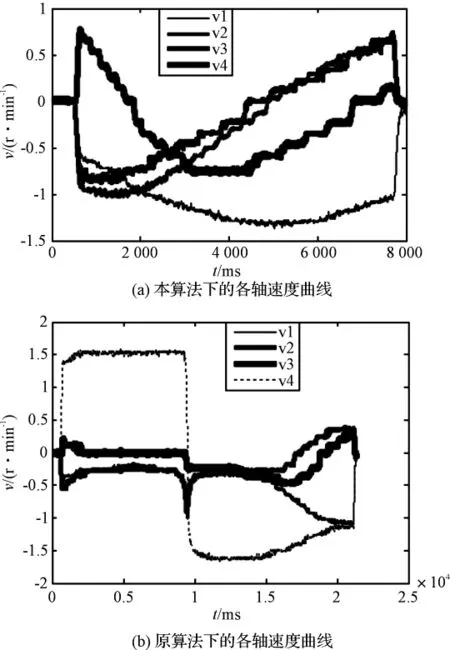
图6 各轴速度曲线对比图

图6(a)、6(b)所对应的笛卡尔空间轨迹是完全一样的。从图6(b)可以看到，在一段较长时间内，第四轴的速度要比其他三轴速度大很多，因此，第四轴每个插补点所转过的角度比其他轴都大很多，有可能产生突变，导致插补的精度下降，同时插补时间也明显增加(约为图6(a)的2倍)。图6(a)中各轴速度较为均匀，不会出现某一轴速度长时间大于其他轴，由此可知各轴插补角度较为均匀，有效地减少了角度突变的可能。由于各插补角度较为均匀，可实现较小步距角的插补，有利于提高精度。

6 结束语

本研究针对6自由度工业机器人，采用分离变量法求其运动学逆解，并根据逆解的特点和机器人的几何结构从逆解中选取最优逆解，将曲线插补中的姿态插补转化为对绕空间中的某根轴旋转的角度的插补，并将以上逆解的改进算法运用到插补算法中。实验结果表明，机器人曲线插补更为精确，有效地避免了各关节角度突变。笔者给出了6参数位姿表示法与位姿矩阵之间的变换算法，由此可以得到雅克比矩阵，用于速度或力矩控制。用户坐标系的建立，使机器人运动空间的定位更加符合和方便用户需要，极大方便了用户的使用。

改进后的算法也存在一些缺点，当机械手的第四轴的旋转范围小于(－180°，+180°)且机械手插补过程中经过奇异点时，容易出现旋转角度超出范围，这些缺点有待于进一步研究解决。

［1］MANOCHA D，CANNY J F.Efficient inverse kinematics for general 6R manipulator［J］.IEEE Transactions on Robotics and Automation，1994，10(5):648-687.

［2］李友虎，叶伯生，朱志红.基于几何法的机器人运动学逆解［J］.武汉船舶职业技术学院学报，2002(1):9-11.

［3］NEPPALLI S，CSENCSITS M A，JONEB B A.A geometrical approach to Inverse Kinematics for Continuum manipulators［C］//Intelligent Robot and systems，2008:3565-6570.

［4］KARLIK B，AYDIN S.An improved approach to the solution of inverse kinematics problems for robot manipulators［J］.Engineering Applications of Artificial Intelligence:The International Journal of Intelligent Real-Time Automation，2000，13(2):159-164.

［5］刘永超，黄玉美，王效岳，等.基于遗传算法的机器人运动学逆解［J］.机器人，1998，20(6):421-426.

［6］王 伟，谢明红，周国义.6-DOF工业机器人逆解优化及其工作空间的研究［J］.机械与电子，2011(1):57-60.

［7］卓扬娃，白晓灿，陈永明.机器人的三种规则曲线插补算法［J］.装备制造技术，2009(11):27-29.

［8］NIKU S B.Introduction to Robotics:Analysis，Systems，Applications［M］.Beijing:Publishing House of Electronics Industry，2004.

［9］PIEPER D L.The kinematics of manipulators under computer control［D］.Stanford:Stanford University cdlege of Engineer，1968:151-157.

［10］殷际英，何广平.关节型机器人［M］.北京:化学工业出版社，2003.