2013年芦山MS7.0地震序列参数的早期特征:传染型余震序列模型计算结果*
蒋长胜 庄建仓 龙 锋 韩立波 郭路杰
1)中国北京 100081 中国地震局地球物理研究所
2)日本东京 106-8569 数理统计研究所
3)中国成都 610041 四川省地震局
引言
据中国地震台网测定,2013年4月20日8时2分46.0秒,四川省芦山县发生MS7.0强烈地震.至4月23日6时,该地震已造成193人死亡,25人失踪,1万2 211人受伤(中华人民共和国中央人民政府,2013).芦山MS7.0地震是继2008年汶川MS8.0地震后在龙门山断裂带上发生的又一次灾害性地震,两次强烈地震的余震区相距仅约45km(刘杰等,2013).因涉及到与汶川MS8.0地震的关系(陈运泰等,2013)及龙门山断裂带南段的地震危险性等问题,芦山地震的发生引起了社会、政府和地震学界的高度关注.
余震序列的衰减特征和激发余震的能力可通过序列的统计参数来表征,不同构造区域、序列类型、主震的震源机制类型、震源区局部构造应力水平及大地热流等地球物理特征都可能表现为序列参数的显著差异(Kaganetal,2010).对余震序列参数尤其是早期参数特征(蒋海昆等,2007)的研究一直是地震学和地球物理学研究的热点问题.近年来,作为“大森-宇津”公式(Omori,1894;Utsu,1961)的推广,“传染型余震序列”(epidemic-type aftershock sequence,简写为ETAS)模型(Ogata,1988,1989,2001)得到长足发展.ETAS模型除可对地震序列参数进行接近真实的估计外,还被用于地震活动平静识别(Ogata,1992,2001;Zhuang,2000)与地震活动的触发(Pengetal,2012)等研究.
与芦山MS7.0地震相关的一个重要科学问题,就是地震序列参数及其表征的震源区地震学特征.本文使用ETAS模型和最大似然法对芦山MS7.0地震序列进行参数估计,并讨论参数估计的可靠性以及参数的地震学含义.
1 时间序列ETAS模型
余震序列随时间的衰减常用修正的“大森-宇津”公式(Omori,1894;Utsu,1961)来表示:

式中,f(t)为t时刻对应的余震发生率,t为主震发生后的离逝时间,μ表示背景地震的发生率,p表示余震序列衰减的快慢,c为主震后余震频次达到峰值时对应的时间,K表示余震的活跃程度.式中的μ,K,c和p均为非负常数.
实际上,真实的余震序列远比简单的修正的“大森-宇津”公式复杂.针对每次余震都可激发自己的余震的情况,Ogata(1988,1989,2001)在“大森-宇津”公式基础上,提出了基于随机点过程的ETAS模型.ETAS模型假设研究区的背景地震发生率μ为常数,所有余震遵从“大森-宇津”公式激发自己的余震,被激发的余震数仅与其“母震”的震级相关,且震级的分布是独立的.ETAS模型假定主震的发生为初始零时刻,在其后的一个观测时间段[0,T]内的地震序列{(ti,Mi);i=1,2,…,N}的强度函数可表示为(Ogata,1988)
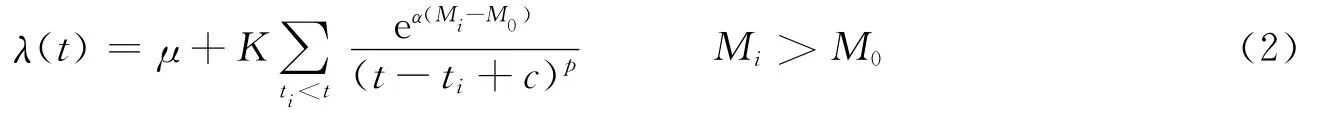
其中,Mi和ti分别表示第i个事件的震级和发生时间;M0为参考震级,一般可取截止震级.p与修正的“大森-宇津”公式中的p有相同的物理含义,均表示序列衰减的快慢,p越大衰减越快,反之亦然.α表示触发次级余震的能力(Ogata,1989,1992).对于震群型序列,一般情况下α<1,而序列中无明显的次级余震时,α则较大(Ogata,2001).
ETAS模型参数可使用最大似然法进行估计.由于主震发生后短时间内主震的波形振幅较大,使得后续余震检测的信噪比显著降低,余震频次难以达到峰值,因此拟合常在[S,T]范围内进行,其中0<S<T.似然函数L的形式为

其中,待估参数为μ,K,c,α,p.尽管上式中的参数在[S,T]内进行拟合,但实际上[0,S]范围内的事件也参与了计算,具体体现在上式右侧的λ(t)中(Ogata,2001).对于模型的适用性检测,常使用赤池准则(Akaike information criteria,简写为AIC)(Akaike,1974)进行判断:

AIC值越小表示适用效果越好.值得注意的是,上式中k为待定拟合参数的数量.因此,AIC准则既考虑了模型对数据的适用程度,也考虑了对增加参数个数提高拟合效果的“惩罚”.ETAS模型研究中常使用AIC准则判断不同模型的拟合效果(Guo,Ogata,1997),以及对拟合变点问题(change-point problem)的讨论(Ogata,1992;Zhuang,2000)等.
2 研究所用资料和序列目录的完整性分析
本研究所用的芦山MS7.0地震序列目录来自中国地震台网中心“全国地震编目系统”提供的《四川地震台网速报目录》①全国地震编目系统.http:∥10.5.202.22/bianmu/index.jsp.查阅日期:2013年5月15日..选用2013年4月1日—5月14日0级以上地震,限定地震序列的空间范围为29.8°—30.6°N,102.6°—103.2°E.
研究中采用“震级-序号”法(Huang,2006;蒋长胜,吴忠良,2011;Zhuangetal,2012)定性讨论芦山地震序列目录的完整性震级Mc.震级-序号法按地震发生时间的先后顺序排序,地震密度较大的区域的连线大致为Mc的时序变化.这种分析一方面避免了主震发生后短期内余震较为密集,在时间轴上难以分析余震监测能力的快速变化;另一方面,由于监测分析工作中的人为因素,Mc在震后短期内常出现分段和不连续性的变化,震级-序号法则易于分辨这种人为因素(图1).由图1a给出的震级-序号点图和放大的子图可见,芦山地震发生后的短时间内,Mc仅为ML3.0左右,其后余震区的监测能力逐渐提升,Mc逐渐减小;至第190个事件,即震后0.31天左右,Mc可达ML2.0.

图1 芦山MS7.0地震序列目录的完整性分析(a)芦山MS7.0地震序列的震级-序号图.子图为序列第1—240个事件的放大图,垂直虚线标出了ML2.0以上地震完整的位置,约为第190个事件,即主震后0.31天;(b)震级-序号法给出的地震密度分布Fig.1 Catalogue completeness of the Lushan MS7.0earthquake sequence(a)Magnitude-rank distribution of the Lushan MS7.0earthquake sequence.Grey subplot shows the partial enlarged view of the first 240events,and the vertical dashed line indicates the completeness of ML≥2.0aftershocks,which is the position of the 190th event or 0.31days after the main shock;(b)Seismic rate distribution given by magnitude-rank analysis
3 芦山MS7.0地震序列的ETAS模型参数的最大似然估计
在对芦山MS7.0地震序列进行ETAS模型参数的最大似然估计时,选定2013年4月1日—5月14日的地震序列,设定Mc=ML2.0,参数拟合所用的时段为震后0.31—24.12天(5月14日24时).由此获得的芦山MS7.0地震序列的ETAS模型参数为μ=0.0000,K=0.009 5,c=0.045 7,α=1.886 4和p=1.220 5,结果如图2所示.图2a为利用最大似然估计获得的ETAS模型条件强度曲线,即单位时间内地震发生率随时间的变化.由该图可见,在震后10天内,序列衰减较为平稳;10天后由于序列地震事件的显著减少,较大余震事件引起的强度曲线变化较为明显.
为检测ETAS模型对实际地震序列的拟合效果,除AIC准则外,一般还常使用“转换时间”域的“残差分析”(Ogata,1988;Daley,Vere-Jones,2003).对条件强度函数λ(t)可采用下式对时间序列{ti}进行转换:

根据上式,{ti}被逐个地转化为{τi},且{τi}服从单位速率的稳态泊松分布(Zhuanget al,2012),经过转化的数据称为“残差点过程”(residual point process,简写为RPP).如果模型与数据拟合得较好,RPP在转换时间-累积图上就表现为线性,接近标准的稳态泊松过程的理论直线.图3a给出了芦山MS7.0地震序列累积地震数与ETAS拟合曲线在“转图2 利用ETAS模型拟合给出的芦山MS7.0地震序列ML2.0以上地震的条件强度曲线(a)和M-t图(b).纵坐标上的频度指每天发生的地震次数
Fig.2 Temporal variation of the conditional intensity from fitting the ETAS model to the LushanMS7.0earthquake sequence with cutoff magnitude ML2.0(a)andM-tplot(b).The frequency on the ordinate axis means the earthquake number per day换时间”域τ的比较情况,即RPP分析结果.由图3b给出的M-τ图可见,芦山MS7.0地震序列在“转换时间”域τ已被转换为稳态泊松分布.实际上就一般强余震预测而言,对“转换时间”域τ的预测和预测效能进行检验可能更有意义(Jiang,Wu,2012).

图3 芦山MS7.0地震序列ML2.0以上地震的累积地震数与ETAS模型拟合曲线的比较(a)累积地震数与ETAS拟合曲线在“转换时间”域τ的比较;(b)M-τ图,τ为将时间转换为稳态泊松分布的“转换时间”Fig.3 Comparison of the observed and modeled cumulative numbers of the Lushan MS7.0earthquake sequence with magnitude larger than ML2.0.(a)Observation(black curve)and ETAS formula(thick gray dashed line)in the transformed time(τ)domain;(b)M-τplot whereτis the transformed time which is according to the stationary Poisson process
4 序列参数早期特征的影响因素分析
由于真实地震序列的复杂性,参数估计的不确定性一直是ETAS模型研究关注的重要问题.例如截止震级对序列分支比(Sornette,Werner,2005)、模型参数的估计偏差(Schoenbergetal,2010)的影响,以及地震序列时空选取对ETAS模型参数估计的影响(Wangetal,2010a)等.为考察芦山MS7.0地震序列ETAS模型参数早期特征的稳定性,本研究从截止震级Mc的选取及拟合截止时间两个角度分别讨论.
4.1 截止震级对ETAS模型参数估计的影响
由于ETAS模型假定每一次地震都可触发其后发生的任何震级的地震,因此,截止震级Mc在确保地震目录完整性的同时,也可能切断了Mc以下地震与以上地震的触发关系,从而造成“链接缺失”现象(Wangetal,2010a).为考察Mc的选取对ETAS模型参数估计的影响,研究中设定Mc=ML2.0,2.1,…,3.0,分别考察模型参数的最大似然估计结果.此外,还采用基于对数似然函数的Hessian矩阵(Ogata,1978)估计拟合参数的标准差,结果见表1.
由表1可见,当Mc自ML2.0—3.0逐渐升高时,参数K总体有减小的趋势,α有明显的线性增加,表明序列触发次级余震的能力随着截止震级的增加逐渐变弱.p值则随Mc的变化不大,约为1.22—1.26,表明在芦山MS7.0地震序列早期阶段,序列衰减快的特征较为稳定.
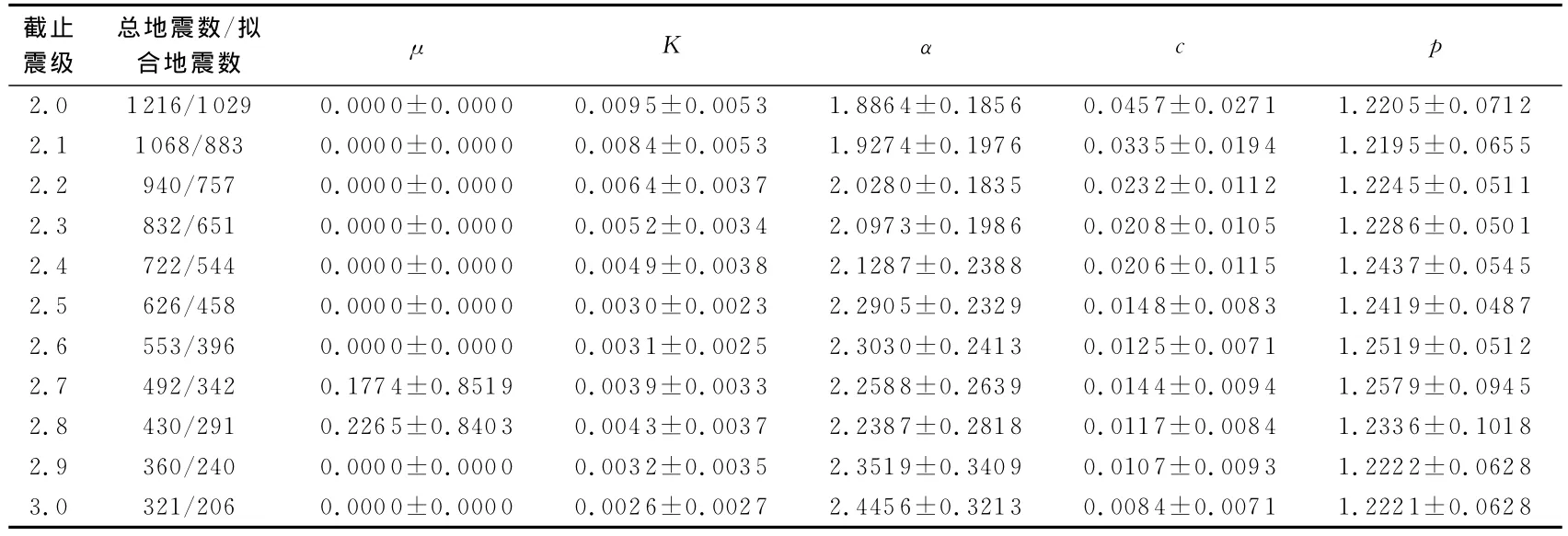
表1 不同截止震级下ETAS模型拟合参数Table 1 Parameters of ETAS model with different cutoff magnitude
4.2 拟合截止时间对ETAS模型参数估计的影响
由于板内地震所处构造运动速率不同,地震序列持续时间存在明显差别(Stein,Liu,2009),震源的破裂特征、断层愈合速度、周边构造场的调整等诸多方面也会使地震序列的衰减特征、激发余震能力等出现明显差异.因此,所用序列的长度或拟合截止时间不同,获得的ETAS模型参数可能不同,拟合参数的标准差也将存在差异(Wangetal,2010b).为考察震后短期内序列参数早期特征的稳定性,设定序列拟合的截止时间tend=[2.0,2.5,3.0,3.5,4.0,5.0,…,23,24.12],利用最大似然法分别进行参数估计.
除考察ETAS模型主要参数α和p外,研究中还考虑了相应的地震序列b值的稳定性.在b值计算中采用最大似然法(Aki,1965;Utsu,1965):

式中,〈M〉为平均震级;ΔMbin为地震目录的震级滑动宽度,一般ΔMbin=0.1.对b值的不确定度δb估计采用Shi和Bolt(1982)给出的方法:
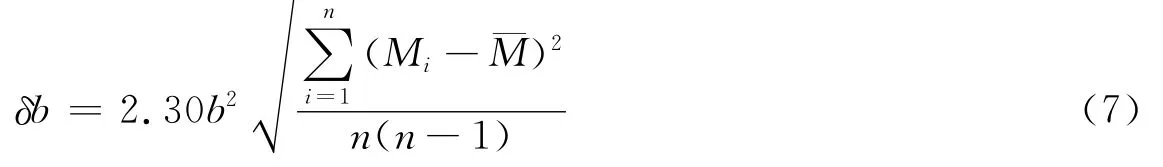
计算获得的α值、p值和b值结果如图4所示.由该图可见,在震后10天内上述参数均存在显著变化,标准差幅值较大.其中α值变化范围为2.47—2.10,p值变化范围为0.93—1.24,b值则逐渐由0.64增加至0.71.在震后10—24.12天(5月14日),α值逐渐减小至1.89,p值逐渐增加至1.22,b值相对平稳地保持在0.72左右.由此可见,在估算芦山MS7.0地震序列的ETAS模型参数时,震后10天内获得的结果随时间变化较为明显,而其后各参数尽管有所变化但总体较为平稳.

图4 ETAS模型参数α,p和b随拟合截止时间的变化(a)和M-tend图(b)Fig.4 Parametersα,pand b against the end time tendin ETAS fitting(a)and the M-tendplot(b)
4 讨论与结论
为考察2013年4月20日芦山MS7.0地震序列参数的早期特征,本文利用ETAS模型和最大似然法进行了参数估计.选用截止震级Mc=ML2.0,拟合所用的时段为震后0.31—24.12天,计算得到α=1.89和p=1.22.序列总体表现为触发次级余震的能力较弱,序列衰减速率较快;利用最大似然法估计的b值也较低,约为0.72,表明余震区应力水平相对较高.
为检测上述结果稳定性,设定Mc=ML2.0,2.1,…,3.0,以及选用不同的拟合截止时间分别进行参数拟合和参数标准差估计.结果表明,截止震级Mc的选取对α和K值影响明显,但对p值影响则较小.此外,震后10天内得到的参数拟合结果随时间变化较为明显,而其后各参数变化总体较为平稳.
根据蒋海昆等(2007)给出的中国大陆294次M>5.0中强震余震序列参数ETAS模型拟合结果,西南地区的平均序列参数为b=0.871,α=0.933,p=0.760;中国大陆地区斜滑型主震对应的平均序列参数为b=0.865,α=0.979,p=0.876;中国大陆M>7.0地震的平均序列参数为b=0.956,α=0.509,p=0.684.与上述结果比较并考虑结果的离散范围,本研究获得的芦山MS7.0地震序列b=0.72,低于上述相同区域(西南地区)、主震类型(逆冲型)和主震震级(M>7.0)的平均结果;α=1.89显著高于上述结果,并高于日本地区板内地震的平均结果(Guo,Ogata,1997),表明该地震对次级地震的激发能力较弱;此外p=1.22也明显高于上述各结果,表明序列衰减速率较快.
本文采用时间序列ETAS模型并重点研究了地震序列参数的早期特征.计算结果显示芦山MS7.0地震序列参数与以往研究的中国大陆震例存在显著差异,可能有两方面原因:一方面是龙门山断裂带南段的构造特点和介质属性,但与2008年汶川MS8.0地震衰减速率和断层愈合过程相比差别较大来看,这种影响可能性很小;另一方面是受区域构造应力场的影响,此次地震的序列参数显示了区域较强的构造应力背景,而这种影响可能造成断层愈合过程较快,或发生强余震、后续强震的可能性较大.但对断层愈合过程的讨论仍需更多直接的观测证据证明.实际上,目前已有多种形式的ETAS模型,例如,基于随机除丛法的时-空ETAS模型(Ogata,1998;Zhuangetal,2002;Zhuang,Ogata,2006),考虑变化的背景地震活动的时间序列ETAS模型(Pengetal,2012)等;本文中的ETAS模型选取主要出于使研究问题尽量简化的考虑.此外,在参数估计中未考虑地震目录中震级等的测定误差,这可能是本研究的不足之处.
本文使用了中国地震台网中心“全国地震编目系统”提供的四川省区域地震台网速报目录,中国地震局“四川省芦山‘4·20’7.0级强烈地震科学考察”总指挥吴忠良研究员对本文给予了指导,周仕勇教授和蒋海昆研究员提出了有益建议.作者在此一并表示感谢.
陈运泰,杨智娴,张勇,刘超.2013.从汶川地震到芦山地震[J].中国科学:地球科学,43(6):1064-1072.
蒋长胜,吴忠良.2011.玉树MS7.1地震前的中长期加速矩释放(AMR)[J].地球物理学报,54(6):1501-1510.
蒋海昆,郑建常,吴琼,曲延军,李永莉.2007.传染型余震序列模型震后早期参数特征及其地震学意义[J].地球物理学报,50(6):1778-1786.
刘杰,易桂喜,张致伟,官致军,阮祥,龙锋,杜方.2013.2013年4月20日四川芦山MS7.0级地震介绍[J].地球物理学报,56(4):1404-1407.
中华人民共和国中央人民政府.2013.民政部:芦山地震已造成193人死亡,25人失踪[EB/OL].[2013-04-23].http:∥www.gov.cn/jrzg/2013-04/23/content_2386791.htm.
Akaike H.1974.A new look at the statistical model identification[J].IEEETransAutomatControl,19(6):716-723.Aki K.1965.Maximum likelihood estimate ofbin the formula logn=a-bmand its confidence limits[J].BullEarthquake ReInst,43(2):237-239.
Daley D D,Vere-Jones D.2003.AnIntroductiontoTheoryofPointProcesses——Volume1:ElementaryTheoryand Methods[M].Second Edition.Springer:New York:17-33.
Guo Z,Ogata Y.1997.Statistical relations between the parameters of aftershocks in time,space and magnitude[J].J GeophysRes,102(B2):2857-2873.
Huang Q.2006.Search for reliable precursors:A case study of the seismic quiescence of the 2000Western Tottori prefecture earthquake[J].JGeophysRes,111(B4):B04301,doi:10.1029/2005JB003982.
Jiang C S,Wu Z L.2012.Testing the forecast of aftershocks:A simple method with an example of application[J].ResearchinGeophysics,2(1):29-33.
Kagan Y Y,Bird P,Jackson D D.2010.Earthquake patterns in diverse tectonic zones of the globe[J].PureApplGeophys,167(6/7):721-741.
Ogata Y.1978.The asymptotic behavior of maximum likelihood estimators for stationary point processes[J].AnnInst StatistMath,30(2):243-261.
Ogata Y.1988.Statistical models for earthquake occurrences and residual analysis for point processes[J].JAmerStatist Assoc,83(401):9-27.
Ogata Y.1989.Statistical model for standard seismicity and detection of anomalies by residual analysis[J].Tectonophysics,169(1/3):159-174.
Ogata Y.1992.Detection of precursory relative quiescence before great earthquakes through a statistical model[J].J GeophysRes,97(B13):19845-19871.
Ogata Y.1998.Space-time point-process models for earthquake occurrences[J].AnnInstStatistMath,50(2):379-402.
Ogata Y.2001.Increased probability of large earthquakes near aftershock regions with relative quiescence[J].JGeophys Res,106(B5):8729-8744.
Omori F.1894.On aftershocks of earthquakes[J].JCollSciImpUnivTokyo,7:111-200.
Peng Y J,Zhou S Y,Zhuang J C.2012.An approach to detect the abnormal seismicity increase in Southwestern China triggered co-seismically by 2004SumatraMW9.2earthquake[J].GeophysJInt,189(3):1734-1740.
Schoenberg F P,Chu A,Veen A.2010.On the relationship between lower magnitude thresholds and bias in ETAS parameter estimates[J].JGeophysRes,115(B4):B04309,doi:10.1029/2009JB006387.
Shi Y,Bolt B A.1982.The standard error of the magnitude frequencyb-value[J].BullSeismolSocAm,72(5):1677-1687.
Sornette D,Werner M J.2005.Apparent clustering and apparent background earthquakes biased by undetected seismicity[J].JGeophysRes,110(B9):B09303,doi:10.1029/2005JB003621.
Stein S,Liu M.2009.Long aftershock sequences within continents and implications for earthquake hazard assessment[J].Nature,462:87-89.
Utsu T.1961.A statistical study on the occurrence of aftershocks[J].GeophysMag,30:521-605.
Utsu T.1965.A method for determining the value ofbin a formula logn=a-bmshowing the magnitude frequency for earthquakes[J].GeophysBullHokkaidoUniv,13:99-103.
Wang Q,Jackson D D,Zhuang J C.2010a.Missing links in earthquake clustering models[J].GeophysResLett,37(21):L21307,doi:10.1029/2010GL044858.
Wang Q,Schoenberg F P,Jackson D D.2010b.Standard errors of parameter estimates in the ETAS model[J].Bull SeismolSocAm,100(5A):1989-2001.
Zhuang J C.2000.Statistical modeling of seismicity patterns before and after the 1990Oct 5Cape Palliser earthquake,New Zealand[J].NZJGeolGeophys,43(3):447-460.
Zhuang J,Harte D,Werner M J,Hainzl S,Zhou S.2012.BasicModelsofSeismicity:TemporalModels[M/OL].Community Online Resource for Statistical Seismicity Analysis.doi:10.5078/corssa-79905851.http:∥www.corssa.org.
Zhuang J,Ogata Y.2006.Properties of the probability distribution associated with the largest event in an earthquake cluster and their implications to foreshocks[J].PhysicalReviewE,73(4):046134,doi:10.1103/PhysRevE.73.046134.
Zhuang J,Ogata Y,Vere-Jones D.2002.Stochastic declustering of space-time earthquake occurrences[J].JAmerStat Assoc,97(458):369-380.

