基于PID 神经元网络的风力发电机组偏航系统研究
张学阳
(华侨大学 信息科学与工程学院,福建 厦门 361021)
0 引言
风电是一种可再生的清洁能源,取之不尽、用之不竭,发电过程不消耗矿产资源,不排放污染物和温室气体,是人与自然和谐共处、实现经济和社会可持续发展的新能源[2]。由于风场中的风向随时会发生变化,所以需要风轮始终对准风向。偏航系统是风力发电机组特有的伺服系统,它是使风轮稳定地跟踪变化的风,保证捕获最大的风能。风力发电机组在发电状态下偏航时会产生陀螺力矩波动,进而引发塔架、叶片等的振动,从而对整个风力发电系统的安全性构成威胁,因此偏航系统不适合频繁起动[3]。此外,近年来风力发电机组的大型化也对偏航系统的稳定性提出了更高的要求。
如果将常规的PID 控制器应用于偏航系统中,偏航执行机构很容易因为频繁动作而损坏[3]。神经网络控制作为智能控制的一个重要分支,是模仿人的思维形式进行的一种自动控制,具有较好的动态性能和较强的鲁棒性,能够有效地改善偏航系统的响应速度,文献[4]中提出,传统PID 控制与神经网络相结合的PID 神经元网络控制器,克服了PID 控制方法和神经网络的缺点[5]。经Matlab编程仿真证明,采用PID 神经元网络设计的偏航系统控制器能够满足控制要求。
1 偏航装置简介
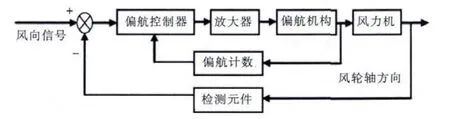
图1 偏航系统闭环控制结构图Fig.1 Structure diagram of yaw system closed loop control
风机的偏航控制系统框图如图1所示[6],风机对风的测量主要是由风向标来完成。当实际的风向与风向标成一定角度时,风向标产生一电信号,偏航控制器采集该信号,经程序计算判定是否偏航。当确定偏航后,计算机发出偏航动作信号,信号经放大后驱动顺偏或逆偏继电器,使偏航电机运行来完成顺时针、逆时针或向上、下向转动对风。当对风结束后,风传感器失去电信号,电机停止工作,偏航过程结束[7]。
2 偏航的神经网络控制
由于风向的随机性,所以偏航系统是一非线性的系统,各种参数也存在时变性。因此,不仅用经典控制理论来解决得不到满意结果,即便是现代控制理论有时也得不到非常满意的结果。而PID 神经元网络控制不需要精确的数学模型,它是一种模仿人的思维形式对难以建立精确模型的对象实施的一种自动控制,是处理推理系统和控制系统中不精确和不确定性的一种有效方法。
2.1 PID 神经元网络结构
PID 神经元网络控制器和被控对象构成的闭环控制系统如图2所示[8];图中X11 是水平角度控制目标,X21 是垂直角度控制目标;y1是控制器水平控制律, y2 是控制器垂直控制律;X12是风轮机水平角度的当前值,X22 是风轮机垂直角度的当前值;上述变量之间关系如图3所示,由于偏航控制系统有两个角度控制量(水平角度和垂直角度),所以选择由两个单神经元网络组成的多神经元网络作为系统控制器。
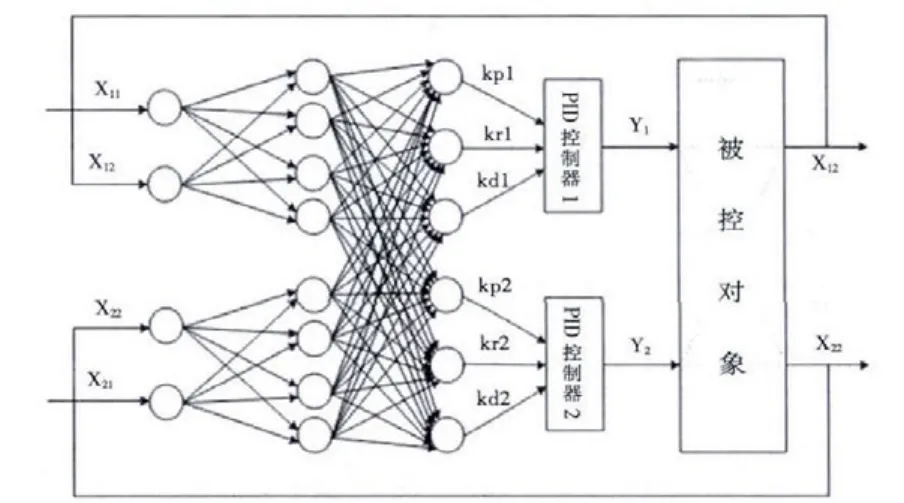
图2 双控制量的BP 神经网络拓扑结构图Fig.2 The topological structure of BP neural network diagram of dual control volume

图3 偏航系统控制器输入输出变量图Fig.3 Diagram of the yaw system input variable
2.2 控制律计算
PID 神经元网络分为输入层、隐含层和输出层,网络输入层为控制量当前值和控制目标,输出量为控制律,各层的输入输出计算公式如下:
(1)输入层:其中包含4个神经元,输出数据等于输入数据。

(2)隐含层:其中包含6个神经元,即2个比例神经元,2个积分神经元,2个微分神经元。

(3)隐含层各神经元输出的计算公式如下:
比例神经元:

积分神经元:

微分神经元

式(1~5)中,s—并联子网络的序号;j—子网络中隐含层神经元序号;xsi(k)—各子网络输入层神经元输出值;ωij—各子网络输入层至隐含层的连接权重值。
(4)输出层:其中包含2个神经元,构成2 维输出量,输出层的输出为隐含层全部神经元的输出值加权和。

式中:h—输出层神经元序号;s—子网序号;j—子网的隐含层神经元序号;usj(k)—隐含层各神经元输出值;ωjk—隐含层至输出层的连接权重值。
2.3 网络权值修正
PID 神经元网络在控制过程中根据控制量采用 “梯度修正法”修正权值,采用粒子群算法优化神经网络初始权值,通过增加动量项的方法提高网络学习效率,可以避免权值在学习过程中陷入局部最优值并有利于提高网络学习效率,从而使控制量快速接近控制目标。
(1)误差计算公式:

式中: yh(k)—预测输出; r(k)—控制目标。
(2)权值修正公式:
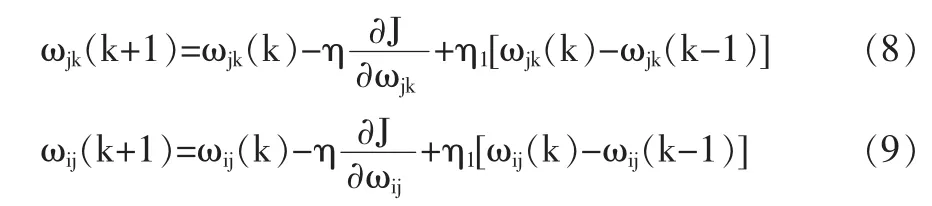
式中:ωij—输入层到隐含层间权值;ωjk—隐含层到输出层间权值;J—控制误差;η,η1—学习速率。
3 偏航系统控制器仿真
根据PID 神经元网络的控制原理,在Matlab 中利用神经网络工具箱编程实现PID 神经元网络双控制变量耦合系统,利用粒子群算法优化初始网络权值,粒子群算法参数设置:种群规模为60,进化次数为40;控制量初始值 [X12,X22]=[0,0],控制目标为 [X11,X21]=[0.6,0.4];仿真时间间隔为0.001 秒,网络权值学习速率为0.05,偏航控制系统仿真效果如图4~5所示。

图4 控制量变化曲线Fig.4 Change curve of control quantity
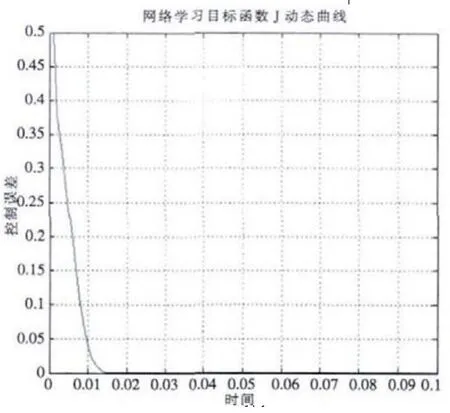
图5 控制误差变化曲线Fig.5 Change curve of control error
4 结果分析
由于风向变化具有随机性和不确定性的特点,而且风力发电机组的偏航控制过程中难以建立准确的数学模型,如果将传统的PID 随动控制器应用于偏航系统中,虽然可满足基本要求,但是响应速度较慢,会导致风能的浪费。本文设计了一种基于神经网络算法的控制器来
完成对偏航系统的控制。仿真结果表明,该控制系统的整体性能要优于PID 控制系统,它能同时满足偏航系统对控制精度和稳定性的要求,有效地消除了系统的超调和振荡,能够快速响应系统的变化,因此可以更好地达到预期的控制目标。
[1]杨伟欢,叶安丽,马鸿雁.模糊控制在风力发电机组偏航控制系统中的应用[J].北京建筑工程学院学报,2011,3.
[2]李毅,温正忠,赵少刚,等.风力发电机偏航系统模糊控制的研究[J].设计·研究·分析,2006,3.
[3]宋建军,张扬,张长安,等.基于模糊控制的风力发电机组偏航系统研究[J].电网与清洁能源,2011,7.
[4]舒怀林.PID 神经元网络及其控制系统[M].北京:国防工业出版社,2006.
[5]杨华.基于神经网络的航空发动机PID 控制[D].西北工业大学,2007.
[6]叶杭冶.风力发电机组的控制技术[M].北京:机械工业出版社,2006.
[7]张嘉英,等.风力发电机组偏航控制系统[J].兵工自动化,2009,11.
[8]汪丽媛,周锐,强鹏翔.基于BP 神经网络整定的多变量PID 控制器设计[J].信息与电脑,2009,12.

