一类二阶变系数线性微分方程的解法

王丽霞

（山西大同大学数学与计算机科学学院，山西 大同 037009）

一类二阶变系数线性微分方程的解法

王丽霞

（山西大同大学数学与计算机科学学院，山西 大同 037009）

研究了利用常数变易法求一类二阶变系数线性微分方程通解的解法，给出通解公式.关键词：二阶变系数线性微分方程；常数变易法；通解

我们知道对于二阶常系数齐次线性微分方程

其中p，q是常数。当(1)的特征方程r2＋py＋q＝0的两个根r1，r2为两个相等的实根,即r1＝r2＝r时, (1)的通解为y＝（C1＋C2x）erx,其中(1)的两个特解分别为y1＝erx,y2＝xerx。

对于一类二阶变系数齐次线性微分方程

其中k（x）,p（x）,q（x）是关于x的函数,利用上述结果[1-3],通过常数变易法给出了其通解的表达式。

定理设二阶变系数齐次线性微分方程

［k（x）y′］′＋p（x）y′＋q（x）y＝0的特征方程r2＋pr＋q＝0有两个相等的实根即r1＝r2＝r时,其中k（x）,p（x）,q（x）是关于x的函数,则方程(2)的通解为

y′1＝rf′（x）erf(x),

y″1＝rf″（x）erf(x)＋r2f′2（x）erf(x)，

将y1，y′1，y″1代人(4)得

由于erf(x)≠0,故(5)可化为.

将y2,y′2,y″2代人(4)得

由于erf(x)≠0,即(7)可化为

对(8)移项整理可得不是常数。

其中C1，C2为任意常数。

证明对(2)进行变形得

即(3)可整理为

设y1＝erf(x)为(2)的一个非零特解,其中r为不为零的常数(在特定条件下r也可为零),f（x）为关于x的函数。

对y1＝erf(x)进行求导可得在 k(x)[rf″(x)+r2f′2(x)]+[k′(x)+p(x)]·[rf′(x)+ q(x)=0

成立的条件下,(9)化为对(10)进行移项整理可得

以f′（2x）除(11)的两端可得即令z＝f′－（1x）,则上述方程成为

此方程是一个非齐次线性方程,先求对应的齐次方程

用常数变易法,把C换为G(其中G是关于x的函数),

代入(12)式，可得则

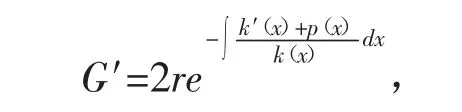
两端积分可得

由z＝f′－1（x），可得

即

则

即方程(2)的通解为

y＝［C1＋C2f（x）］erf（x）。

则

[1]东北师范大学微分方程考研室.常微分方程[M].北京：高等教育出版社,2005.

[2]严文军.常数变异法求解一类一阶非线性常微分方程[J].产业与科技论坛,2011，10(14)：175-176.

[3]梁洪亮,徐少华.一类二阶变系数常微分方程的初等解法[J].数学的实践与认识，2009,39(20)：213-216.

〔责任编辑 高 海〕

The General Solution to a Kind of Second Order Linear Differential Equation with Variable Coefficient

WANG Li-xia
(School ofMathematics and Computer Science,Shanxi Datong University,Datong Shanxi，037009)

The solvingmethod of general solution to a kind of second order linear differential equation with variable coefficien was studied in the paper.With constant variation adopted,the fomula of general solution to second order linear differential equation with variable coefficientwas presented.

second order linear differential equation with variable coefficient;constant variation；general solution

O175.1

A

2012－12－08

王丽霞（1979－），女，山西大同人，硕士，讲师，研究方向：微分方程。

1674-0874（2013）03-0010-02