基于BP神经网络的温度预测方法

李会兵

（西安机电信息技术研究所，西安,710065）

0 引言

在引信的环境试验中，热源的距离、温度的传输介质等因素对于引信的实际工作温度影响很大，目前主要依靠人工经验或者简单的数据处理方式（线性关系）来判断引信的实际工作温度。温度的测量精度不高，不能够及时的反应引信工作环境的实际温度，测温的延时较大，有可能会导致热源温度与引信的实际工作温度误差较大，使其长时间处于极限工作状态，增加了损坏概率，降低了产品的可靠性。因此，本文介绍一种基于BP神经网络的温度预测方法，对引信的实际工作温度进行预测。

传统的温度测试方法主要有：1）直接测试法，该方法响应速度较慢，不能及时反映温度的变化规律；2）基于试验数据和线性回归的温度预测方法，该方法需要大量的实验数据预先建立模型，数据的获取存在较大困难，使该方法的应用受到一定的限制。因此，本文提出了一种基于BP神经网络的温度预测方法。

1 背景

1.1 传统的环境温度测试方法

传统的环境温度测试方法主要是通过微控制器采集温度传感器，通过内部校准程序对传感器的值进行校准，最后通过显示模块进行显示。具体简单模型如图1所示。

图1 传统的温度测试方法

传统的测试方法中，数据处理模块比较简单，概括起来主要有两种情况，（1）利用温度的线性标定来确定传感器的输出与温度之间的关系，利用插值法求解温度值，误差较大，不能较好的反应温度瞬时变化的过程。（2）主要利用采用以前积累的若干数据，利用线性回归的进行曲线拟合，得到若干条温度曲线，能够反应温度的变化率，但是灵活性较差，前期需要大量的数据积累，可推广性不强。

1.2 BP神经网络

BP（Back Propagation）网 络 是 1986年 由 Rumelhart和McCelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层（input）、隐层(hide layer)和输出层(output layer)。其典型的模型如图2所示。

图2 BP神经网络典型模型结构图

图3 基于BP网络的温度预测模型

2 BP神经网络的温度预测方法

2.1 输入输出

环境试验温度测试原理的普通模型如图2所示，该系统中温度传感器为热敏电阻。

图2 温度测量模型

由图2可知，该测量模型的输入为瞬时温升，输出为传感器的测量温度。从温度测试的角度出发，温度预测的关注点是测试温度和热源实际温度之间的关系。因此，预测模型的输出因子是传感器的输出温度，输入因子为：热源温度变化率dt、热源与传感器的距离l、散热系数st、传感器的热特性f(t)。对于时变温度控制系统，因素热源温度变化率dt和传感器的热特性f(t)起主导作用。

于是传感器的输出温度可以表示为：

对于温度测量而言，由图2可知，其温度的变化由瞬时温升引起的，可以忽略散热系数的影响，因此，其测量温度可以表示为：

(1)、(2)式中： f1、f2为非线性功能函数。

2.2 BP神经网络

在输入因子中，热源温度变化率dt必须实时测量，通常由温控箱来模拟实现；热源与热敏电阻的距离l可以直接测量，通常一次安装结束，l为一常量；散热系数st则需要由散热介质决定，一般为空气，也可以看做定值；热敏电阻热特性f(t)由传感器特性标定得出。

本系统采用BP神经网络建立温度预测模型。输入层节点数m=3，输出层节点数n=1。隐含层采用试凑法确定为20。隐层、输出层神经元的转移函数选用sigmoid函数。网络结构如图3所示。

BP网络算法分为两部分：一是信号的正向传播过程，即训练信号由神经网络的输入层经隐层处理后传向输出层，其间每一层神经元的状态只影响下一层的神经元的状态；二是误差(E(t))的反向传播过程，即采用梯度下降的最小方差学习方式，将误差反向传播，不断调节网络中神经元之间的连接权重，使误差最终达到最小。但当梯度下降的最快方向与误差曲面最小点方向偏离较大时，参数到达最小点的路径将加长，以致网络学习效率低，速度慢。为克服这种不足，本文采用自适应学习速率(η(t))调整法。其调整公式如下：

2.3 基于BP神经网络的温度测试模型

根据输入输出的设计和BP神经网络的设计，本文建立一种基于BP神经网络的温度预测模型，如图4所示。

图4 基于BP神经网络的温度预测模型

在本温度预测模型中，利用BP神经网络的温度预测算法替代了传统的数据处理模块，利用神经网络中的自适应学习的方法对温度传感器进行预测，与直接测试法相比，有明显的优势。

3 基于BP网络的温度预测方法仿真

由于引信的形状、大小、材料等不同，为了简化描述方法，本文以汽车轮毂刹车过程中温度的变化为例，利用MALAB进行仿真试验，验证本方法的有效性。

利用传统的直接测试法，在模拟环境中进行温度数据采集，以获得的试验数据为基础，在MTLAB中仿真，对BP神经网络模型进行训练。

通过实验，分别在温度变化率为25、35和50三种情况下，安装距离为10mm，获取了部分数据，如表1、表2、表3所示。

表1 温度变化率为△t/s =25°

表2 温度变化率为△t/s =35°

表3 温度变化率为△t/s =50°

由表1、2、3中可以看出，利用直接测试方法，当温度的瞬间变化率较大时，温度测试值与实际温度存在明显的滞后，相对误差高达51%。

将上述的试验数据用于BP神经网络的训练与检验。在表1、2、3中各选一组数据作为检验样本，如表4所示，其他为训练样本。

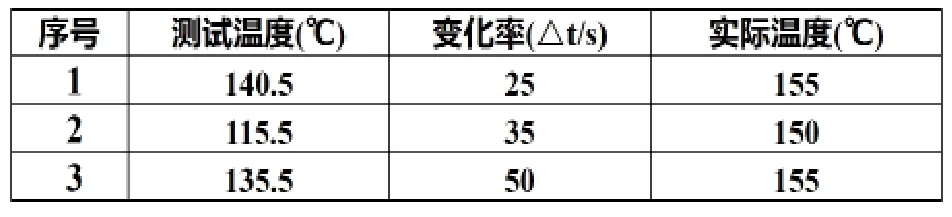
表4 检验样本

在MTLAB中，通过软件编程，设置神经网络的训练次数为2000次，训练精度为10-3，隐含层的节点为20。

训练误差如图5中所示，训练误差最大的地方出现在温度变化率发生变化，同一温度变化率时，训练误差趋近于零。预测输出如图6所示，通过训练样本对BP神经网络进行训练，利用测试样本得到其温度预测结果。将BP神经网络温度预测方法与直接测试法进行比较，结果如表5所示。

图5 BP网络训练误差

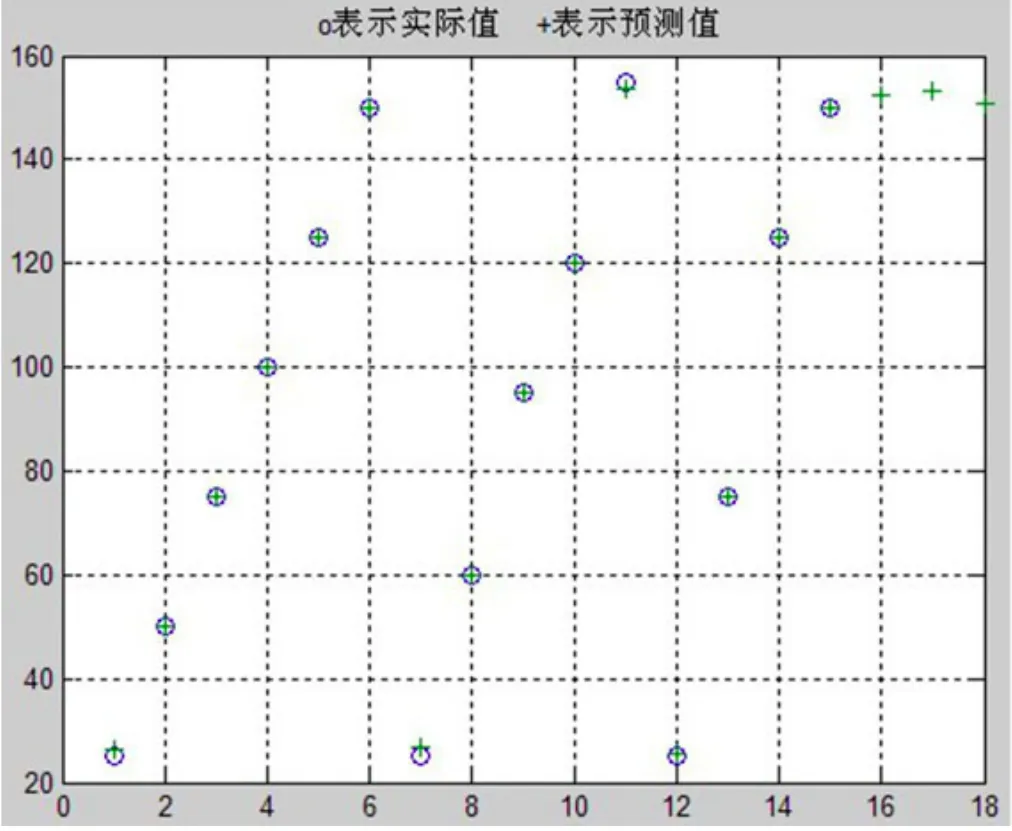
图6 BP网络预测输出

表5 预测结果误差分析表

由表5可见，BP神经网络的温度预测方法，系统的预测精度小于3.2%，比传统测量方法的测量精度有明显的提升，同时测温的延时有了明显的改善。

4 结论

本文提出了基于BP神经网络的温度预测方法。该方法通过测量瞬时温度变化率，利用BP神经网络的温度预测模型，对温度进行预测。在MATLAB中仿真表明，该方法在训练2000次后即达到设定精度，温度预测精度小于3.2%，验证了该方法的有效性。为了进一步提高温度预测精度，下一步将增加数据量，对BP神经网络的训练算法进行深入研究。

[1]周永乾.基于单片机的汽车刹车片实时温控系统[J].科技咨询.2008(18):98-99.

[2]陈飞等.长大下坡路段重型车辆刹车毂温度预测模型研究[J].

[3]李华成等.交通冲突量的BP神经网络预测方法[J].交通与计算机.2006.24(6):71-72.