矩形隧道中电磁波传输损耗收敛阈值频率分析

郑红党，王亚男

（中国矿业大学 信电学院，江苏 徐州221008）

在隧道中存在的波模必满足：

矩形隧道中电磁波传播模式理论以文献［1］为基础，研究了隧道形状、尺寸和隧道壁的电参数对电磁波的传播特性的影响，所做分析仅针对基模或部分波模［2－5］。仅用基模或部分波模的传输特性来分析电磁波的特性是不够准确的，几何光学与波模理论分析结果的分歧也在于此［6－7］。近期，Sun Zhi等研究了多波模理论并结合阴影衰落建模［8－9］，其仿真结果与实验结果更为接近，但在其研究中没有考虑波模数量的问题，一旦传播环境改变，有效的传输波模数目也会随之变化。

波模理论有必要进一步推导与分析，首先应推导出随着隧道环境变化，传输波模个数的公式，再对隧道内的传播特性进行分析，于隧道无线通信系统建设提供明确的参考。

1 波模理论基础

矩形隧道中传输的主要模式为：水平极化波Eh与垂直极化波Ev。若隧道的宽度为a，高度为b，隧道壁的相对介电常数为ε，根据麦克斯韦方程，可以得到水平极化波Eh的各场量的表达式［1］：

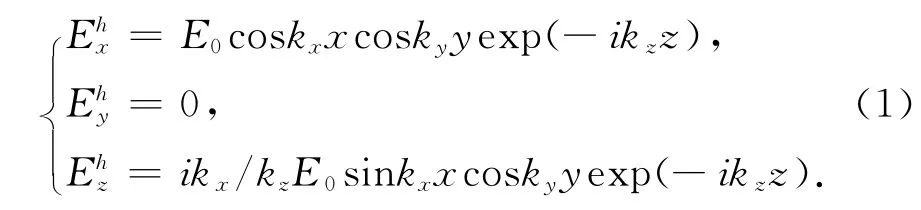
其中，色散系数kx，ky，kz满足：

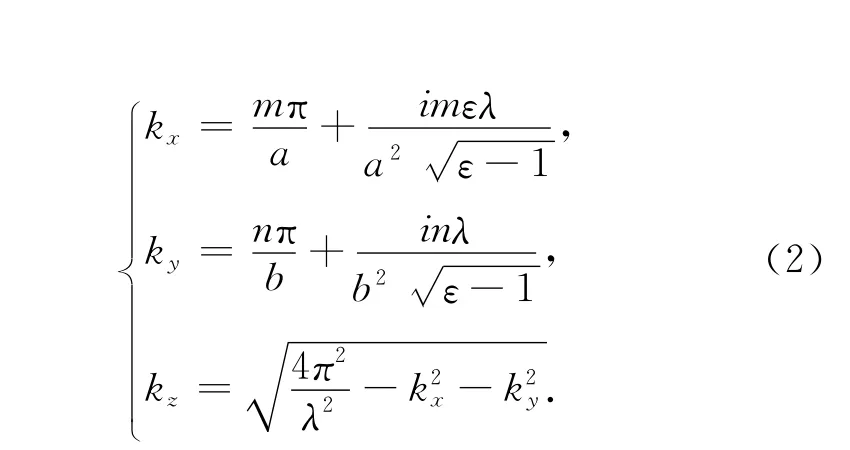
垂直极化波Ev的各场量的表达式为：

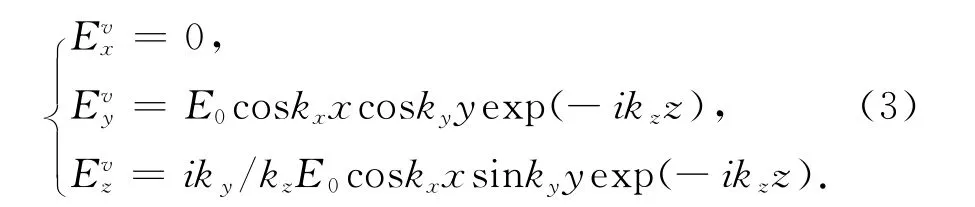
其中，色散系数kx，ky，kz满足：

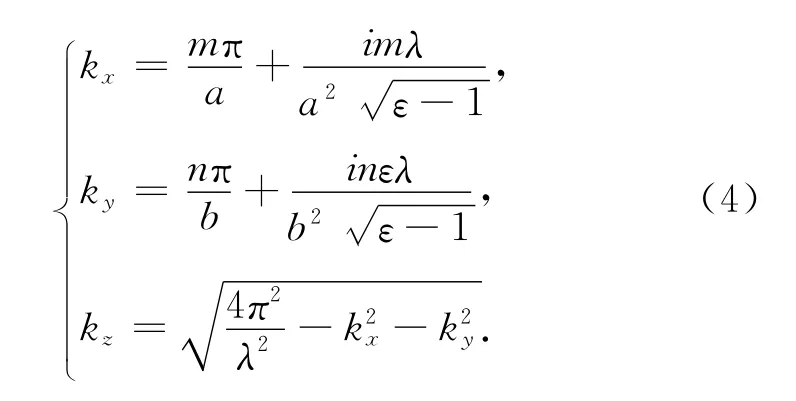
式中：m为波模在水平方向的半波数；n为波模在垂直方向的半波数。

kz中的虚部表示了波模在z方向的衰减，用dB表示水平极化波Eh的衰减系数有：

通过交换式（5）中的下标，可得到垂直极化波Ev的衰减系数：

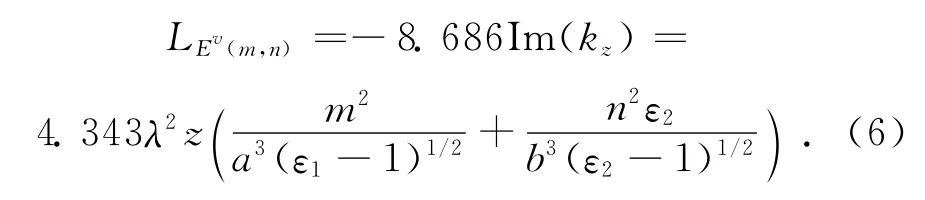
由式（5）和式（6）可见，仅对各个波模来说频率越高所对应的衰减系数越小，并且隧道横截面尺寸越大，衰减系数越小。

2 传播模式个数的推导

隧道中电磁波传输时的波模数目并没有文献给出准确的公式，一些文献也只是通过仿真来确定在某一特定环境下，需要考虑的波模数目。但随着环境的变化，波模数目将会改变。

分析式（2）式（4），色散系数kx，ky的虚部，由于传输波长选择小于巷道尺寸，由此忽略虚部则：

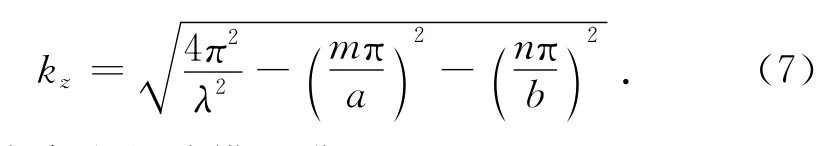
在隧道中存在的波模必满足：

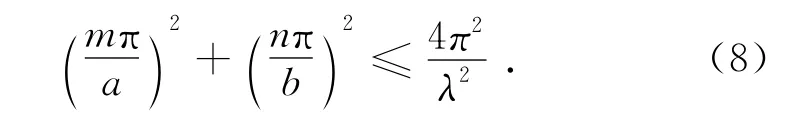
进一步推导可得：

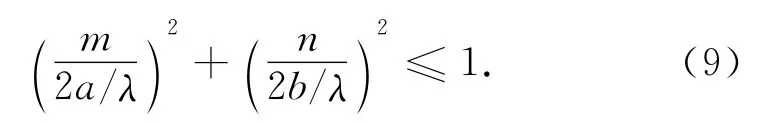
由公式（11）可知，在隧道中传输的波模的模数（m，n）必在以长轴为2a／λ，短轴为2b／λ的椭圆内，又因为m，n非负，所以总的波模个数M 为此椭圆的1／4面积即：

波模的数目与波长的平方成反比即随频率的平方而增长，符合文献［10］的结论。

3 波导传输损耗推导

以水平极化波为例，不考虑天线的方向性，每个波模的携带能量相等，总的介质波导传输损耗为：

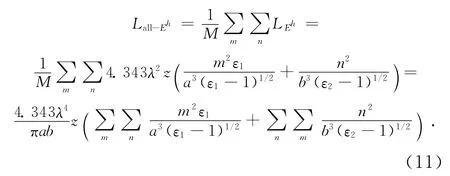
当隧道横截面尺寸远远大于电磁波波长时，则公式（11）第一项累加和可化为积分形式：

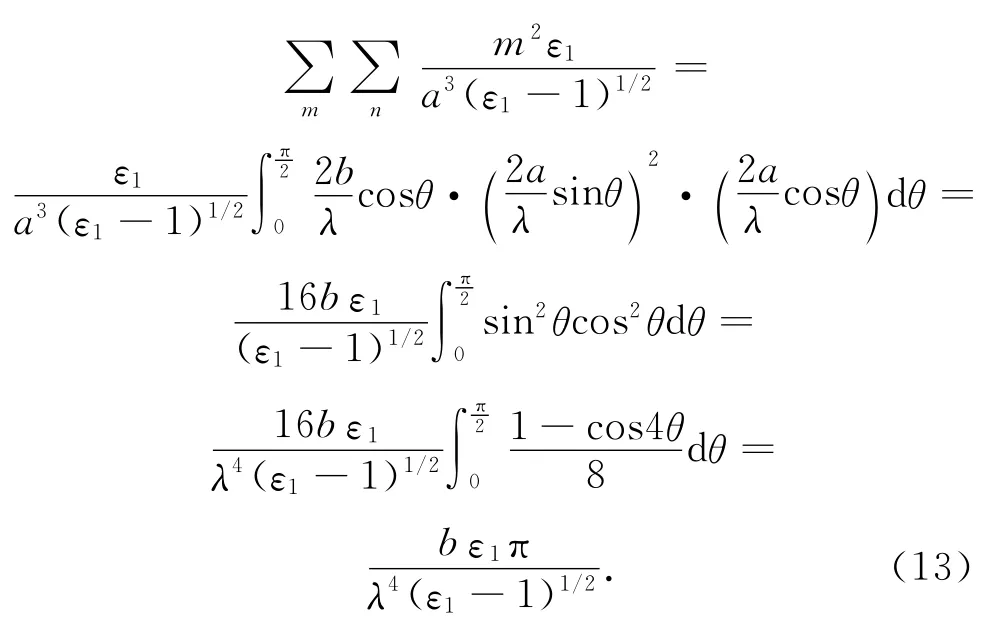
同理，求公式（11）的第二项累加和得：

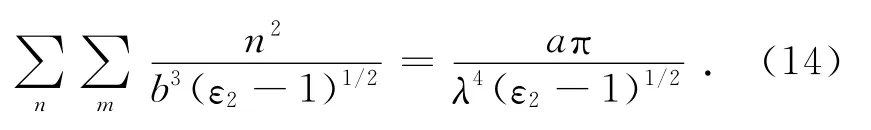
式（13）和（14）代入式（11）可得水平极化波考虑所有可能出现的波模时总的损耗为：

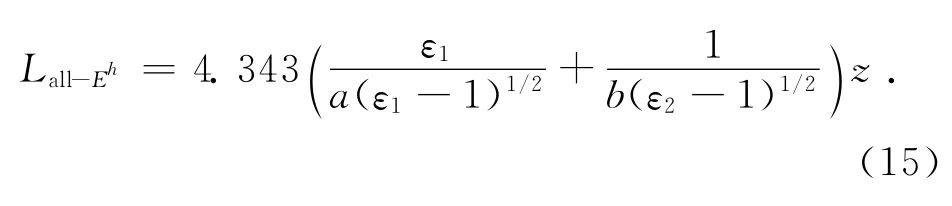
用同样的方法计算垂直极化波的波导损耗为：

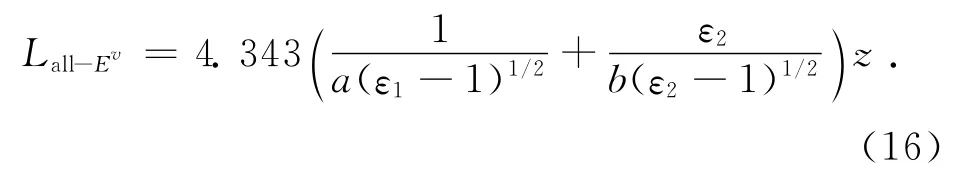
由式（15）与式（16）知，随着频率的升高，当波长远远小于截面尺寸时，总波模损耗收敛于一个稳定值，且这个稳定值与波长无关。即存在一个阈值频率，当发射频率增加到此阈值频率，再提高发射频率，对于减少波导损耗的作用不大。当隧道截面尺寸增加时，介质波导引起的损耗将减少。

因此，求出收敛阈值频率是对于载频的选择有着重要的指导意义。下面通过仿真分析影响此阈值的因素。

4 仿真与分析

为了取得波长或频率阈值的共性，分别对宽为10m，高为5m的大隧道和宽为1m，高为2m的小隧道进行了仿真分析。

图1仿真了电磁波衰落与激励波模数的关系，可以看出在大巷道与小巷道中电磁波随波模数目变化的衰落趋势是基本相同的。当激励的波模数目大于200时，电磁波衰落值就很接近于式（15）式（16）给出的收敛值，即当波模数目大于200时，电磁波的介质波导损耗的计算可以用式（15）式（16）代替。也说明随着发射频率的提高，介质波导衰落不会再随之明显的减小，为了减小散射与倾斜度的衰落，则最佳发射频率应取收敛点处的频率。

图1 隧道中电磁波衰落与激励波模数的关系

文献［11］通过测量数据也从另一侧面说明了这个结论，“当巷道截面等效半径与波长相差不大于10倍时（大于或小于），巷道截面尺寸对无线传输的影响较大，当巷道截面等效半径远远大于波长时，巷道截面对无线传输的影响微弱”。由于波模数目与巷道截面成正比，当巷道截面较小时，也就是激励的波模数目较少时，截面积的大小对无线传输的影响大，当截面尺寸继续增大时，激励的波模模数目超过一定的数值时，巷道截面的大小对无线传输影响较小，与本文的结论是一致的。

根据以上分析，把激励波模数目M＝200代入公式（10），可以得到阈值波长，从而计算出阈值频率，作为发射频率的参考。表1为频率阈值参考表。

文献［11］中也指出煤矿最佳传输频率为900 MHz，煤矿巷道横截面尺寸为8m2附近，这也与本文所得结果一致。

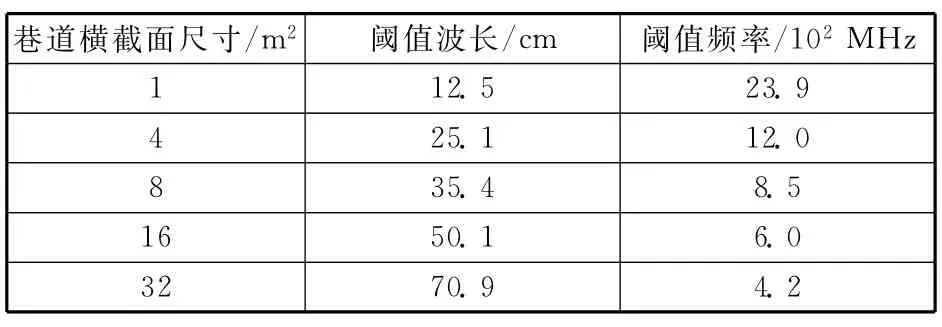
表1 收敛阈值参考表

5 结论

论文运用波模理论推导分析出在矩形隧道中随着发射频率的提高，介质波导传输损耗趋于一个收敛值，其大小取决于隧道尺寸，而收敛的趋势则取决于激励的波模数。对不同尺寸隧道的仿真表明，当激励的波模数目达200左右时，传输损耗均近似等于收敛值，对应的频率即为收敛阈值频率。这与文献［10］经过测量得到的结论基本一致。收敛阈值频率对隧道内载频的选择有着重要的指导意义，当载频小于收敛阈值频率的波导损耗会随着频率的提高而迅速减小，当频率大于收敛阈值时，波导传输损耗是一个平稳值。

［1］ Emslie A，Lagace R，Strong P．Theory of the propagation of UHF radio waves in coal mine tunnels［J］．IEEE Transactions on Antennas and Propagation，March，1975，23（2）：192－205．

［2］ 成凌飞，孙继平．矩形隧道围岩电参数对电磁波传播的影响［J］．电波科学学报，2007，22（3）：513－517

［3］ 杨维，李滢，孙继平．类矩形矿井巷道中 UHF宽带电磁波统计信道建模［J］．煤炭学报，2008，33（4）：467－472．

［4］ 孙继平，成凌飞，张长森．电导率对巷道中电波传播的影响［J］．辽宁工程技术大学学报，2007，26（1）：96－98．

［5］ Dudley D G，Lienard M．，Mahmoud S．F．，Degauque P．Wireless propagation in tunnels［J］．IEEE Antennas and Propagation Magazine，2007，49（2）：11－26．

［6］ 张申．帐篷定律与隧道无线数字通信信道建模［J］．通信学报，2002，23（11）：41－50．

［7］ 郑红党．煤矿井巷电波传播理论和MIMO信道建模关键技术研究［D］．徐州：中国矿业大学，2010．

［8］ Zhi Sun，Ian F．Akyildiz，Gerhard P．Hancke，Capacity and Outage Analysis of MIMO and Cooperative Communication Systems in Underground Tunnels［J］．IEEE Transactions on Wireless Communications，2011，10（11）：3793－3803．

［9］ Zhi Sun，Ian F．Akyildiz．Channel Modeling and Analysis for Wireless Networks in Underground Mines and Road Tunnels［J］．IEEE Transactions on Communications，2010，58：1758－1768．

［10］ 保罗·德隆涅．王椿年，戴耀森，高怀珍等译．漏泄馈线和地下无线电通信［M］．北京：人民邮电出版社，1988．

［11］ 孙继平．矿井无线传输的特点［J］．煤矿设计，1999（4）：20－22．