辉光放电等离子体特性的实验研究

张青兰，张彩霞

(太原理工大学物理与光电工程学院，太原030024)

等离子体是由大量的带电粒子组成的非束缚态的宏观体系，是物质的第四态。等离子体有许多独特的物理、化学性质，例如温度高、粒子动能大;具有类似金属的导电性能;化学性质活泼，容易发生化学反应;具有发光特性，可以用做光源［1］。因此等离子体技术的应用十分广泛，如磁流体发电、等离子体切割、等离子体光源和等离子体显示，等等。等离子体还为表面材料、半导体材料的生成和制备提供了良好的环境［2-6］。准确测量等离子体参数，是空间探测、航天器防护等领域的关键环节［7］。

辉光放电等离子体属于非热力学平衡等离子体，也称冷等离子体，属于工业应用中最广泛的等离子体之一。一方面，电子具有足够大能量使反应物分子激发、离解和电离;另一方面，反应体系又得以保持低温，使反应体系能耗减少，并可节约投资。电子温度主要在1～20 eV之间，电子密度范围为1012～1025m－3。

本文通过Langmuir单探针法研究了空气辉光放电等离子体参数的分布特性，对实验中得到的数据采用两种方法进行处理，并对影响等离子体参数分布的因素进行研究。

1 实验原理

单探针法是将一个小的金属电极作为探针封入等离子体中，以放电管的阳极或阴极作为参考点，改变探针电位Up，测出相应的探针电流Ip，就可得到探针电流与其电位之间的关系，即探针伏安特性曲线，如图1所示。

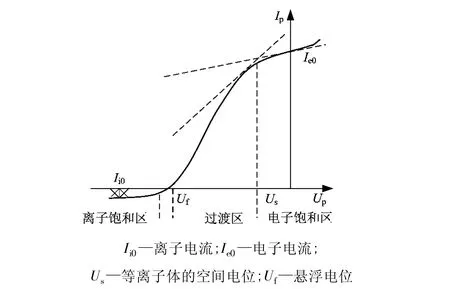
图1 探针的伏安曲线示意图

根据Ip-Up曲线的特征把曲线划分为三部分：电子饱和区、过渡区和离子饱和区。在电子饱和区(Up－Us≫0)，探针周围形成电子鞘，探针收集的是电子电流，离子被排斥。随着外电压的正增加，探针电流趋向饱和电子电流Ie0;在离子饱和区(Up－Us≪0)，探针周围形成离子鞘，探针收集的是离子电流，电子被排斥。随着外电压的负增加，探针电流趋向饱和离子电流Ii0;在过渡区(Up－Us＜0)，探针周围将形成离子鞘，离子鞘将阻挡电子向探针运动，只有能量大于鞘层排斥能的电子才能到达探针形成电子电流，假定等离子区内电子的速度服从麦克斯韦分布，则减速电场中靠近探针表面处的电流为［8］：

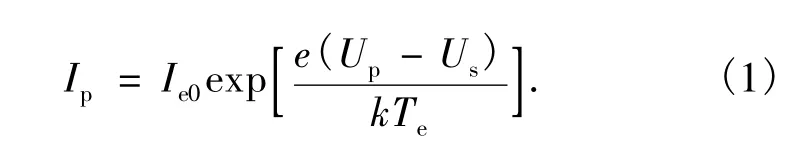
式中：Te为等离子区中的电子温度;k为玻耳兹曼常数。

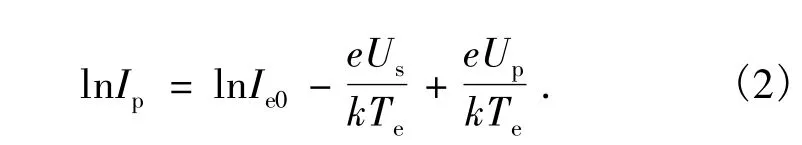
其中：

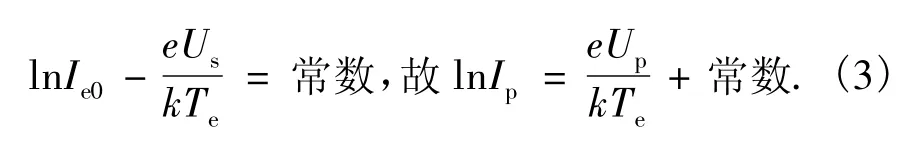
由式(3)可知，在过渡区ln Ip与Up成直线关系，如图2半对数曲线中从Uf到Us的对应曲线部分。直线的斜率tanφ：

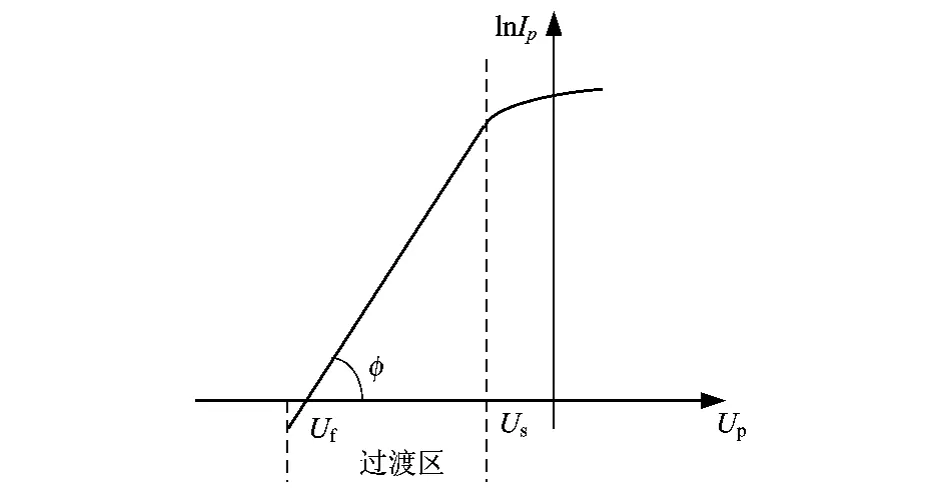
图2 ln I p随U p变化的关系曲线示意图

式中：ne为等离子区中的电子密度;¯ve为电子的平均速率;S为探针裸露在等离子区中的表面面积;me为电子的质量;k为玻耳兹曼常量。

根据单探针法测得伏安特性曲线，由该曲线做出对应的半对数曲线ln Ip与Up，再根据半对数曲线直线部分的斜率即可求得电子的温度Te，进而求得等离子区中的电子密度ne．

本文利用湖南湘潭大学技术科学研究所制造的ED-2型等离子特性测量仪研究了辉光放电等离子体的特性。

2 实验结果及讨论

2.1 实验数据处理方法

根据实验原理，实验中应先保证管中空气在合适的气压与合适的放电电压下产生辉光放电等离子体。通过电位器改变探针上的电位，进而改变探针电流，记录探针电压及对应探针电流。图3为探针在13 Pa、1 kV的伏安特性曲线。

图3 探针在13 Pa，1 kV条件下的伏安特性

等离子体特性参量的大小与过渡区数据密切相关，过渡区起点为悬浮电位Uf，此时对应Ip=0，可从数据或图中看出Uf=－105.75 V。末端为等离子体的空间电位Us。求Us有两种方法：

1)可由指数增长端曲线上延和线性增长端曲线下延的交点决定［1］。但实验数据未必理想，从图2看出线性增长端不明显，无法通过交点求得Us，而从半对数曲线中可明显看出曲线拐点。这时由于改变探针电位的电位器不是十分容易控制电阻特别缓慢的变化，导致从图3探针的伏安特性曲线看不到由过渡区到电子饱和区的拐点，而取对数后将大大弱化数据间的差距，便可清楚地看到拐点，如图4．从图4看出，过渡区的半对数数据点线性关系并不十分好，但由过渡区向电子饱和区的拐点大致可看出Us=－20.5V．由此可找出过渡区数据的始末端，从而由过渡区数据拟合直线(以下简称半对数曲线)求出斜率，如图5．

图4 探针在13 Pa，1 kV条件下整个区间的半对数曲线

2)可以通过等离子体I-V特性曲线的一次和二次微商来求得。一次微商的最大值以及二次微商为0的点对应于等离子体空间电位，如图6。图7为其对应得到的过渡区数据的拟合直线及对应直线方程。比较图5、图7，说明两种方法求得的斜率相差不大。等离子体中的电子温度分别为11.69，12.26 eV。但前者方法由于只靠目测，或由指数增长端对应的半对数数据点手动拟合直线的上延和线性增长端半对数数据点手动拟合直线下延的交点决定，结果总免不了与实际的Us有所错位。相比之下后者结果更可靠易得。以下实验中均采用第二种方法求Us。

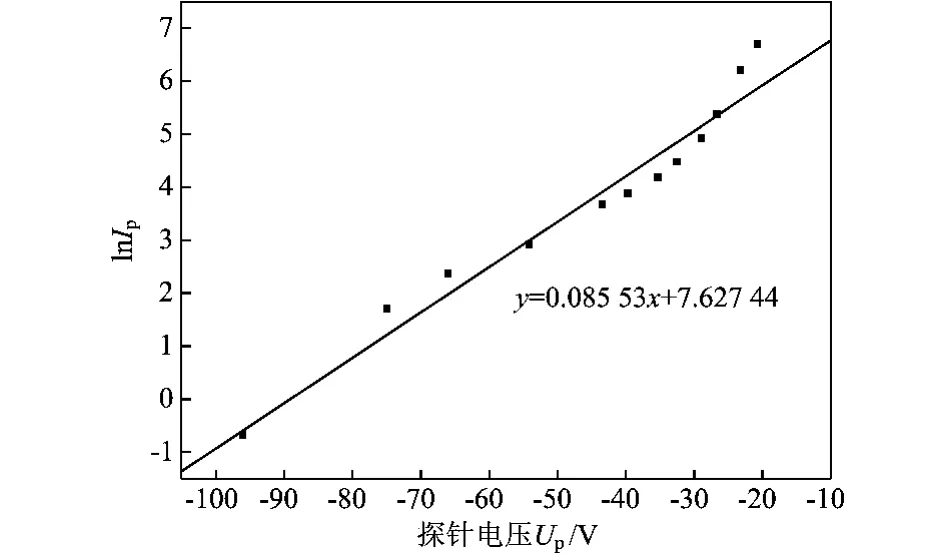
图5 探针在13 Pa，1 kV条件下过渡区的半对数曲线

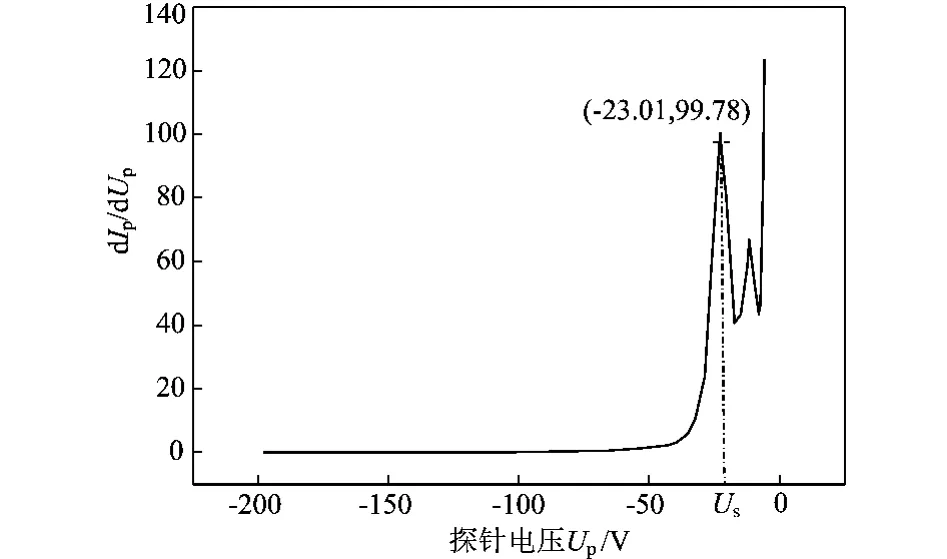
图6 I p-U p特性曲线的一次微分

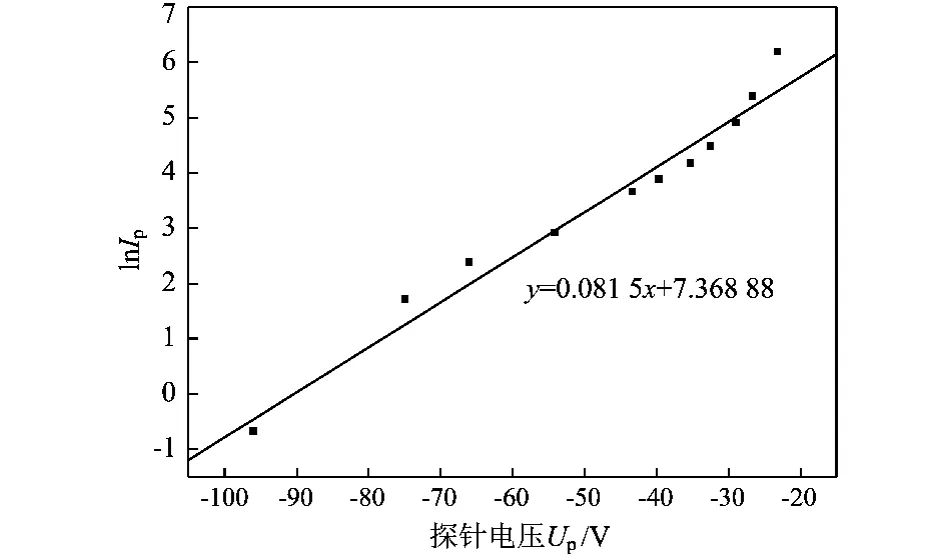
图7 探针在13 Pa，1 kV条件下的半对数曲线

2.2 相同气压不同电压下等离子的特性

图8为探针在一定气压10 Pa而放电电压不同时的伏安特性曲线，图9为对应的半对数曲线。从图8可知随着放电电压的增加，曲线左移、上移。在可比部分说明相同探针电压下放电电压越高探针电流越大。在730 V的探针伏安曲线比较正常，而在800 V、900 V的探针曲线比较失真，探针在该气压、放电电压条件下的伏安特性曲线中饱和电子流区不明显或看不到。实验中也发现有时实验的曲线既无饱和离子流区又无饱和电子流区，这一问题有待于进一步研究。

图8 探针在不同放电电压下的伏安特性曲线

图9 探针在不同放电电压下的半对数曲线

根据式(4)、(5)，由图9中拟合直线的斜率求得在730V、800V、900V的不同放电电压下，电子温度及浓度见表1。

表1 在同一气压10Pa、不同放电电压条件下等离子体中电子的温度与浓度

在式(5)中，裸露在等离子区中的探针表面面积S由探针的直径D=1.159 mm，深入到等离子体中的长度l内≈3 mm求得。

从表1数据中可看出，等离子体在800，900 V时的饱和电子流与电子的浓度有差别，但差别不大。总的来说，放电电压越高，电子温度越低，而电子浓度越大。随着放电电压的增大，电子在高压电场中获得的能量增大，粒子之间碰撞更加频繁，电子与正离子和原子碰撞概率增加，从而会有更多电子从原子中被激发出来，电子数目增加，即电子密度增大。实验中也发现：当气压一定，若逐渐提高放电电压，等离子层数由多变少，而颜色渐渐变浓，说明等离子浓度增大。在较高压电场中，能量大于离子鞘层排斥能的电子较多，到达探针形成的电流增大，致使随电压的增加曲线上移。由于电子与正离子和原子碰撞频率的增加，电子的能量消耗会比较快，从而导致电子温度有所下降。

2.3 相同电压不同气压下等离子的特性

图10为探针在放电电压为800 V一定而气压不同时的伏安特性曲线，图11为对应的半对数曲线。从图10可看出随着气压的增加曲线左移、上移。在可比部分说明相同探针电压下气压越高探针电流越大。

图10 探针在不同气压下的伏安特性曲线

图11 探针在不同气压下的半对数曲线

根据式(4)、(5)，由图11中拟合直线的斜率求得在5，10，20 Pa的不同放电气压下，电子温度、浓度分别见表2。

表2 在同一放电电压、不同气压条件下等离子体中电子的温度与浓度

从表2可看出，随气压的增高电子温度下降，电子密度增大。气压增加时，放电气体的密度增加，电子的平均自由程减小，电子与其他粒子、原子和正离子碰撞的概率增加。更多的电子从原子中被激发出来，进而电子密度增加。在此过程中电子不断消耗能量，导致电子温度下降［9］。电子密度增加，则电子克服离子鞘层排斥能的概率增加，探针电流增大，曲线上移。

3 结论

本文通过Langmuir单探针法研究了空气辉光放电等离子体参数的分布特性，通过数据分析说明利用等离子体I-V特性曲线的一次微商的最大值点求得等离子体的空间电位结果可靠。对影响等离子体参数分布特性的放电电压、气压研究表明：放电电压越高，电子的温度越低，密度越高;气压越高，电子的温度越低，密度越高。

［1］ 赵青，刘述章，童洪辉．等离子体技术及应用［M］．北京：国防工业出版社，2009：1-8，322-327．

［2］ 张谷令，王久丽，杨武保，等．内表面栅极等离子体源离子注入TiN薄膜及其特性研究［J］．物理学报，2003，52(9)：2213-2217．

［3］ 刘元富，张谷令，王久丽，等．脉冲高能量密度等离子体法制备TiN薄膜及其摩擦磨损性能研究［J］．物理学报，2004，53(2)：503-506．

［4］ Zhan R J，Wen X H，Zhu X D，et al．Adjustment of electron temperature in ECR microwave plasma［J］．Vacuum，2003，70：499-503．

［5］ Fujiwara N，Sawai H，Yoneda M，et al．Determination of the EEDF by Langmuir probe diagnostics in a plasma excited at ECR above a multipolar magnetic field［J］．Plasma Sources Sci Technol，2001，10： 181-190．

［6］ Ikushima T，Tochitani G，Fujita H．Low-pressure deposition of diamond by electron cyclotron resonance microwave plasma chemical vapor deposition［J］．J Crystal Growth，2000，211： 216-219．

［7］ 刘晓东，郑晓泉，张要强，等．低温等离子体的诊断方法［J］．绝缘材料，2006，39(2)：43-46．

［8］ 吴先球，熊予莹．近代物理实验教程［M］．北京：科学出版社，2010：171-178．

［9］ 俞哲，张芝涛，赵建森．Langmuir双探针诊断Ne辉光放电管电子密度［J］．物理实验，2010，30(1)：1-5．