基于自然指数模型的机床定位误差建模与实时补偿*
张 毅,杨建国,李自汉
(上海交通大学机械与动力工程学院,上海 200240)
0 引言
随着制造业对加工精度要求的不断提高,近年来针对如何进一步减小数控机床的误差进行了一系列研究。研究表明:无论是传统的三轴数控机床,还是引入了旋转轴的多轴数控机床,机床定位误差都是最重要的误差来源。在机床实际加工过程中,定位误差在最终形成的加工误差中所占比例可高达70%[1]。尤其是在大、中型机床中,定位误差对加工精度的影响更为显著。因此,对定位误差进行有效的测量、建模和补偿,是提高机床运动性能和加工精度的首要途径。
机床定位精度受到机床零部件加工精度、装配精度以及机床温度场变化引起的热变形的综合影响。传统的螺距误差补偿只能进行恒温条件下的定位误差补偿,并不考虑温度变化对定位误差的影响,因此,在机床的实际加工过程中,随着机床温度的不断变化,补偿精度会逐渐降低。国内外学者对机床误差和温度场变化之间的关系做了大量研究。Pahk等人[2]用多元回归分析方法建立了机床定位误差预测模型,通过补偿提高了机床定位精度。王维等人[3]对一台立式加工中心的定位误差进行了全温度范围内的误差建模和补偿研究,取得了良好的补偿效果。此外,杨建国[4]、Wu[5]和张琨[6]等人也在这方面进行了理论和试验探索,研究了机床定位误差的影响因素及其变化规律。
然而,以上模型基本都将机床热误差和温度场的变化近似视为线性变化规律,没有充分考虑到机床热变形是一个复杂的、时变的非线性过程[7-8],所以其模型预测精度有待于进一步提高。本文在对大量试验数据进行分析的基础上,提出了基于自然指数模型的机床定位误差建模方法,建立了定位误差与机床坐标位置、环境温度变量及机床关键构件温度变量之间的非线性预测模型,可以对不同温度条件下的定位误差做出预测,并在一台机床上进行了实际误差补偿试验,大幅提高机床定位精度。
1 滚珠丝杠传动机构及热源分析
滚珠丝杠传动机构是数控机床的重要传动部件,负责将伺服电机的旋转运动转化为工作台(或主轴)的平移运动。图1所示为常见的机床平动轴滚珠丝杠传动机构,主要由伺服电机、联轴器、前端轴承、丝杠螺母、丝杠和后端轴承构成。通常来说,滚珠丝杠机构的加工精度、装配精度以及由温度变化引起的热误差都是降低机床定位精度的主要误差来源。其中,前两种误差来源不会在机床的加工过程中发生变化(或者变化相对较小),可以视作几何误差,属于静态误差的范畴;而由温度变化引起的热误差则会在机床的加工过程中随着温度的变化而发生改变,属于动态误差范畴。因此在对机床定位误差进行补偿时,需要综合考虑几何误差和热误差的影响。

图1 滚珠丝杠传动机构
从图1中可以看出,滚珠丝杠传动机构主要有四大热源:伺服电机功率损耗产生的热量、丝杠前、后端轴承的摩擦发热,以及螺母在丝杠上来回运动的摩擦发热。要研究机床热误差与温度场分布之间的关系,就必须对这四个主要热源的温度数据进行实时采集,这里分别用 Tmotor、Tb1、Tb2和 Tnut来表示。此外,机床所处环境温度也会对机床热误差造成一定影响,所以需要测量环境温度Tamb。几个主要热源产生的大量热量会在机床零部件内部进行热传导,也会和周围空气之间发生对流传热,形成复杂的温度场分布情况,引起滚珠丝杠的热膨胀变形,并最终导致不同温度条件下的定位误差各不相同。相关文献表明[7-8],机床的热变形(误差)和温度场之间存在复杂的非线性变化规律,下面将对定位误差的变化规律和影响因素做进一步研究。
2 定位误差变化规律分析及建模
2.1 机床关键构件温度对定位误差的影响
为了全面了解机床定位误差在不同温度条件下的变化规律,本试验以五轴机床的X轴为例,首先在机床冷态时,用激光干涉仪测量定位误差,然后让机床以一定的进给速度进行热机,每隔30min重新测量定位误差,直到机床达到热平衡状态。与此同时,通过温度传感器实时测量各关键测点的温度变化。图2所示为从机床冷态开始到热平衡过程中不同时刻的各关键测点的温度变化曲线。图3所示为不同时刻的X轴定位误差曲线。

图2 不同时刻的机床关键测点的温度变化曲线
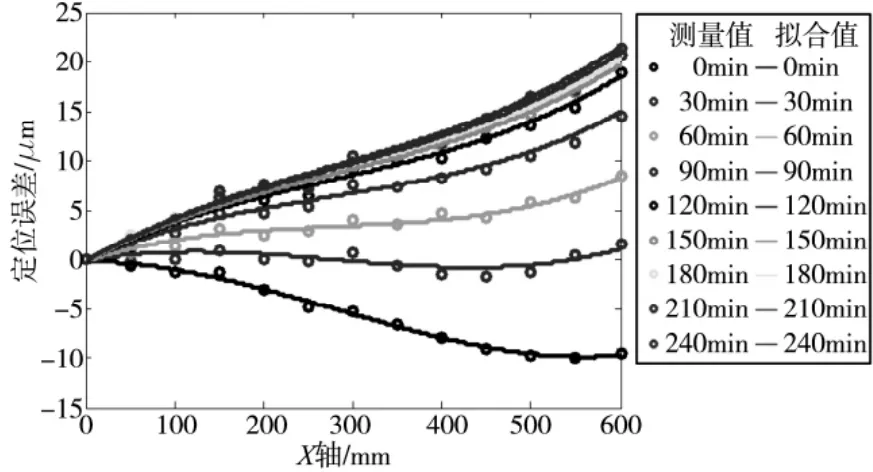
图3 不同时刻的机床X轴定位误差曲线
从图2可以看出,在机床开始运行阶段,各测点的温度增长速率较快,说明机床产热量大于散热量;随着机床的不断运行,各部件的产热量和散热量基本趋于相等,温度增长速率减缓,并在约135min之后基本稳定在某一温度值左右波动。其中,丝杠螺母,前、后端轴承均表现出了这样的变化规律,当到达热平衡时,各自的温度分别稳定在33℃、38℃和36℃左右。然而,在240min的运行过程中,伺服电机的温度一直保持较快增长,且没有明显的变缓和到达热平衡的趋势,最高温升将近35℃。不同于滚珠丝杠和前后轴承的摩擦生热,伺服电机的热量主要来源于功率损耗,和伺服电机的配置参数、负载等有关,而且电机与滚珠丝杠之间存在一定的距离,可以认为电机生热对丝杠的热膨胀影响不是很大,从测量得到的温度和定位误差数据分析来看,两者之间的确不存在明显的数学关系,所以在误差模型中,可以不考虑伺服电机温度的影响。
本组测量试验是在ISO 230-3[9]推荐的标准环境温度(20℃)下进行的,因此在0min时(机床处于冷态时)测量得到的定位误差,可以认为是与温度无关的几何误差,主要由机床构件的加工精度和装配精度决定,属于静态误差。随着机床运行时间的增长,各部件的温度逐渐升高,使得X轴的定位误差也发生了改变。从图3中可以看出,不同时刻的定位误差曲线形状基本相同,但是误差曲线的整体变化趋势(可用误差曲线的一次拟合斜率来描述)随着温度的升高而逐渐变大,因此所有的定位误差曲线构成一个“扇形图谱”,即:以进给轴原点为中心,随着机床的不断热机,定位误差曲线尾部逐渐上翘,从而形成一簇形状相似的误差曲线。
基于以上分析,可以将定位误差分成两个组成部分,如式(1)所示,一部分为几何误差EG,用来描述定位误差曲线的基本形状;另外一部分为热误差ET,用来描述定位误差曲线随温度的整体变化趋势。EG和ET分别可由式(2)和式(3)来表达。
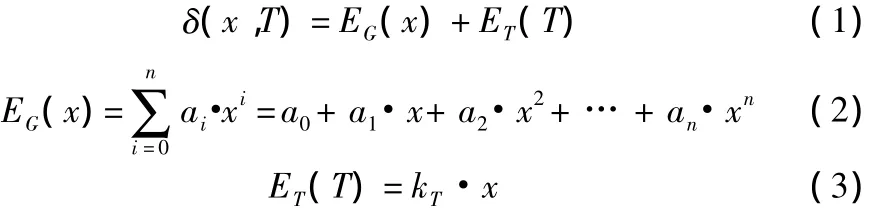
式中:δ表示X轴的定位误差;x表示X轴的坐标位置;T表示与X轴有关的关键温度测点构成的温度向量;n表示几何误差拟合多项式的阶次;kT表示与温度向量T有关的热误差系数。
对于几何误差部分,一个重要的问题是确定拟合多项式的阶次。阶次太低,拟合精度不高;阶次太高,会带来较大的计算负担,不利于误差的实时补偿,同时也容易形成过拟合现象,影响模型的鲁棒性。表1列出了不同阶次的多项式对0min时的定位误差的拟合精度对比,不难看出,多项式阶次越高,拟合精度越好,但是由于四次多项式和三次多项式的拟合精度已经非常接近,为了简化误差模型,这里选取n=3作为X轴定位误差几何部分的最终拟合阶次。*SSE:误差平方和;RMSE:均方根误差

表1 定位误差几何部分多项式拟合精度对比
对于热误差部分,kT是唯一需要确定的模型参数,它决定了定位误差曲线的整体变化趋势。需要注意的是,这里将0min时测量得到的定位误差曲线作为基准曲线(kT=0),其余时刻定位误差曲线的热误差系数kT都是相对于基准曲线而言的。通常来讲,环境温度对机床的热变形影响是统一的、均匀的,该部分试验主要研究的是不同机床构件局部热变形对热误差的影响,因此在计算各关键测点的温度变化时应该以当前环境温度作为基准,具体定义为:

表2列出了不同时刻定位误差曲线的热误差系数和关键测点的温度变化情况。从图2和表2不难看出:丝杠螺母与前、后端轴承的整体温度变化趋势基本相同,而且丝杠螺母与滚珠丝杠通过螺旋运动副直接接触,两者之间的温度变化情况存在较大的关联性,为了简化模型,可以考虑只用ΔTnut来描述整个滚珠丝杠运动机构的温度变化趋势。

表2 定位误差曲线热误差系数和各关键测点温度变化

图4 热误差系数随丝杠螺母温度变化测量值及拟合曲线

式中:kT表示随ΔTnut变化的X轴定位误差曲线的热误差系数;表示其初始值表示达到热平衡状态时的稳定值;
表示影响X轴定位误差的温度常量,该常量通常与滚珠丝杠的材料特性、装配结构及散热条件等有关。
利用最小二乘法可以确定式(5)中的各项模型参数。通过计算结果和图4可知:当 ΔTnut=τ=4.6℃时,kT可增长到热变形稳定状态时的63%,随着机床的不断升温,kT可最终达到0.0549。
2.2 环境温度对定位误差的影响
如上所述,机床内部热源引起的热变形通常是局部的、时变的和非线性的,而环境温度对机床的热变形影响则是整体的、相对稳定的和线性的。为了研究不同的环境温度对机床定位误差的影响,该部分试验仍以X轴为例进行研究。
图4显示了不同时刻定位误差曲线的热误差系数随丝杠螺母温度变化的曲线。从图中可以看出:在机床升温的初始阶段,热误差系数kT增长速度较快,随着机床的不断热机运动,kT增长速度逐渐放缓,并趋于稳定,当ΔTnut增长到约12℃时,kT基本维持在0.05左右波动,即达到热变形平衡状态。
基于以上分析,可以发现kT与ΔTnut的变化情况基本符合“先快后慢再稳定”的自然指数模型增长规律,因此可由式(5)来描述两者间的数学关系:
首先在标准环境温度中测量X轴的定位误差,然后环境温度每升高或降低2℃,用激光干涉仪进行一次全行程范围内的定位误差测量。在18℃ ~26℃的环境温度变化范围内,共测得5条定位误差曲线,如图5所示。其中,环境温度的变化量定义为:


图5 不同环境温度下的X轴定位误差曲线

表3 定位误差曲线热误差系数和环境温度变化对应关系
从图5中可以得出以下结论:
(1)环境温度的改变能引起机床定位误差的显著变化。如果需要控制或提高机床定位精度,就必须严格控制环境温度(如:放置在恒温室内)或者对由环境温度变化引起的热误差进行预测和补偿。在实际加工环境中,控制环境温度通常会带来较大的开销,因此对这部分误差进行补偿具有重要意义。
(2)当环境温度变化时,沿X轴线各点的定位误差变化趋势基本一致,只是变化量大小有所不同。
(3)所有不同环境温度条件下的定位误差曲线同样构成“扇形图谱”,而且环境温度的变化量和定位误差曲线的热误差系数kT基本呈线性关系。这是因为环境温度对于整个机床而言是均匀温度场,对每个机床构件的影响基本相同,所以环境温度导致的热膨胀变形可近似看作线性变化过程。
表3列出了定位误差曲线热误差系数和环境温度变化测量值的对应关系。通过最小二乘法可以确定二者之间如式(7)所示的数学拟合模型,拟合曲线如图6所示。
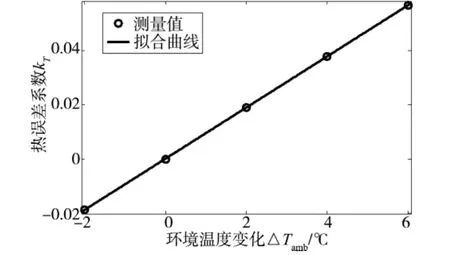
图6 热误差系数随环境温度变化测量值及拟合曲线
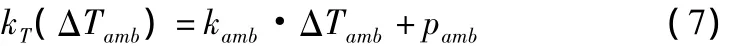
式中:kT表示随ΔTamb变化的X轴定位误差的热误差系数;kamb表示拟合模型的一次项系数;pamb表示拟合模型的常数项。
2.3 基于自然指数模型的定位误差建模
通过上述不同温度条件下的定位误差测量试验,掌握了机床定位误差的变化规律和影响因素,将式(1)~式(7)进行综合,可以得出X轴定位误差的数学模型:
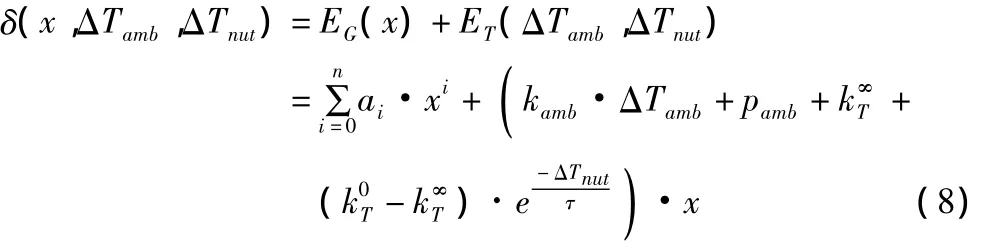
根据测量得到的定位误差数据和温度数据,采用最小二乘法对上式的所有参数进行求解,可以得到该机床X轴定位误差的具体模型。
3 误差模型对比及实时补偿试验验证
为了验证本文提出的基于自然指数模型的机床定位误差建模方法的有效性,下面将和传统的多元回归分析方法进行模型预测精度的对比,并在如图7所示的机床上进行实时误差补偿试验。

图7 激光干涉仪测量X轴定位误差
在多元回归分析模型中,也将X轴的定位误差分为两个部分:几何误差EG和热误差ET。对于EG,采用X轴坐标位置的多项式进行拟合;对于ET,则采用多元线性回归的方法进行建模。选取环境温度变化量ΔTamb、丝杠螺母温度变化量ΔTnut及前端轴承温度变化量ΔTb1作为影响热误差的主要温度变量,可以建立如式(9)所示的定位误差模型:
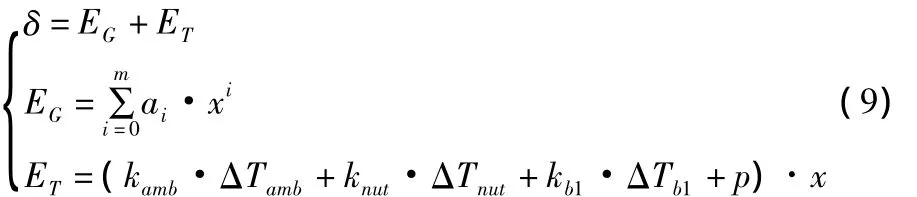
仍然采用以上测量试验的数据确定式(9)中的各项系数。为了验证两种误差模型在任何温度条件下的预测精度,试验选择环境温度为23℃,并且经过一段时间的热机运动,X轴丝杠螺母温度升温约5℃,在此温度条件下测量得到如图8所示的定位误差曲线,并和两种模型的误差预测曲线进行对比。可以看出:基于自然指数模型的机床定位误差模型比多元线性回归模型具有更高的预测精度。表4所示为两种模型的预测残差数据统计,从中也可看出基于自然指数的定位误差模型预测精度更高。
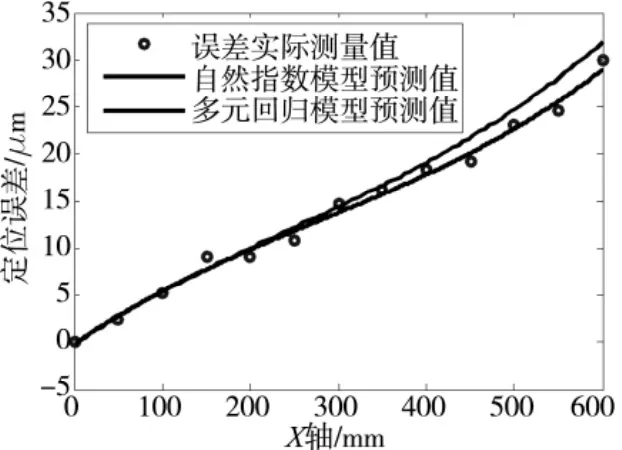
图8 误差测量值及两种误差模型预测值对比曲线

表4 误差模型预测残差统计数据对比/μm

图9 补偿前后X轴定位误差曲线对比
本试验用自行研发的机床误差实时补偿系统通过数控系统提供的外部机械原点偏移功能[4]对定位误差进行实时补偿,补偿前后的定位误差曲线如图9所示。值得注意的是,补偿后的X轴定位误差值和图8及表4中的自然指数模型预测值残差略有不同,这是因为补偿精度不仅取决于误差模型的预测精度,还和机床的伺服系统控制参数、运动部件的惯性、部件间的摩擦系数等因素密切相关。尽管如此,通过误差补偿也可将X轴定位精度提高约91%,补偿前定位误差绝对值的最大值为29.9μm,补偿后最大值仅为2.5μm。因此误差实时补偿试验证明:该误差模型及其补偿方案具有较高的应用价值。
4 结束语
本文通过对机床定位误差进行测量、建模和补偿研究,可以得到如下结论:
(1)机床定位误差不仅受到机床零部件加工精度、装配精度等因素的影响,而且受到机床温度场变化的影响。
(2)基于自然指数模型的机床定位误差建模方法可以描述热误差和温度场之间的非线性变化规律,在从机床冷态开始到热平衡的整个过程中均具有较高的预测精度。该模型可以根据不同的环境温度和丝杠螺母温度对定位误差做出预测,通过实时误差补偿能够大幅提高机床运动精度。
[1]Mayr,J.,Jedrzejewski,J.,Uhlmann,E.,etc.Thermal issues in machine tools[J].CIRP Annals-Manufacturing Technology.2012.
[2]Pahk,H..Lee,S.Thermal error measurement and real time compensation system for the CNC machine tools incorporating the spindle thermal error and the feed axis thermal error[J].The International Journal of Advanced Manufacturing Technology.2002,20(7):487 -494.
[3]王维,杨建国,姚晓栋,等.数控机床几何误差与热误差综合建模及其实时补偿[J].机械工程学报,2012(7):165 -170,179.
[4]杨建国.数控机床误差综合补偿技术及应用[D].上海:上海交通大学,1998.
[5]Wu,C.W.,Tang,C.H.,Chang,C.F.,etc.Thermal error compensation method for machine center[J].The International Journal of Advanced Manufacturing Technology.2012,59(5):681 -689.
[6]张琨.CK6430数控车床几何与热误差实时补偿研究[D].上海:上海交通大学,2012.
[7]Yang,H..Ni,J.Dynamic neural network modeling for nonlinear,nonstationary machine tool thermally induced error[J].International Journal of Machine Tools and Manufacture.2005,45(4 -5):455 -465.
[8]Ramesh,R.,Mannan,M.A..Poo,A.N.Error compensation in machine tools-a review:Part II:thermal errors[J].International Journal of Machine Tools and Manufacture.2000,40(9):1257 -1284.
[9]ISO230-3:Test code for machine tools-Part 3:Determination of thermal effects[S],2007.

