因子分析法在社会环境影响评价中的应用
徐 敏
(山西清源环境咨询有限公司,山西 太原 030012)
引 言
社会环境影响评价是识别、监测和评价建设项目的各种社会影响,分析当地社会环境对拟建项目的适应性和可接受程度,评价建设项目的社会可行性,促进利益相关者对项目投资活动的有效参与,规避项目社会风险的重要工具和手段[1]。通过对项目进行社会环境影响评价,可以在一定程度上确定项目建设对当地社会环境所带来的有利和不利的影响。针对不利因素采取措施,可以减少项目产生的不利影响和受损人群,也可以进一步明确项目所产生的有利影响是否能维持项目所在地区的可持续性发展。
1 社会环境影响评价指标体系
评价指标体系是对评价对象系统的反映。由于社会环境影响评价指标体系是从多个视角和层次反映特定评价客体数量规模与质量水平的,所以,社会环境影响评价指标体系是一个信息系统。社会环境影响评价指标体系是对评价客体系统的水平和规模的反映,它们是两个对应的系统。因此,建立评价指标体系之前,应该对评价客体进行深入的分析研究,把握评价客体系统中各元素的关系[2-4]。
本文以怀仁县清凉河城市湿地公园建设项目为例,从经济效益、社会效益、环境效益、资源利用等方面来进行评价指标体系的建立,如第51页表1所示。
2 建设项目社会环境影响评价模型
建设项目评价指标筛选现有评价方法包括层次分析法和模糊数学综合评判法。层次分析法和模糊数学综合评判法虽然是应用数学原理进行权重的确定,但是基于人为的赋值,结果带有一定程度的主观性,这就使得综合评价结果不具有唯一性和客观性,在指标的设置上主要着重广义的社会环境影响评价方面,不够全面,从而会导致一个综合效益比较好的项目,只因为社会效益中的某一方面而不被选择;或者一个综合效益一般甚至很差的项目,只因为社会效益比较好就被选择。而建设项目的社会环境影响评价应该建立在综合评价的基础上来进行。
2.1 建设项目因子分析
因子分析法通过分析研究中所测量一组变量(称原始变量)的相关系数矩阵,将这些变量进行分类,每一类中的变量具有相同的本质(称为因子),从而了解这组变量的基本结构,以对指标体系中的指标进行检验。
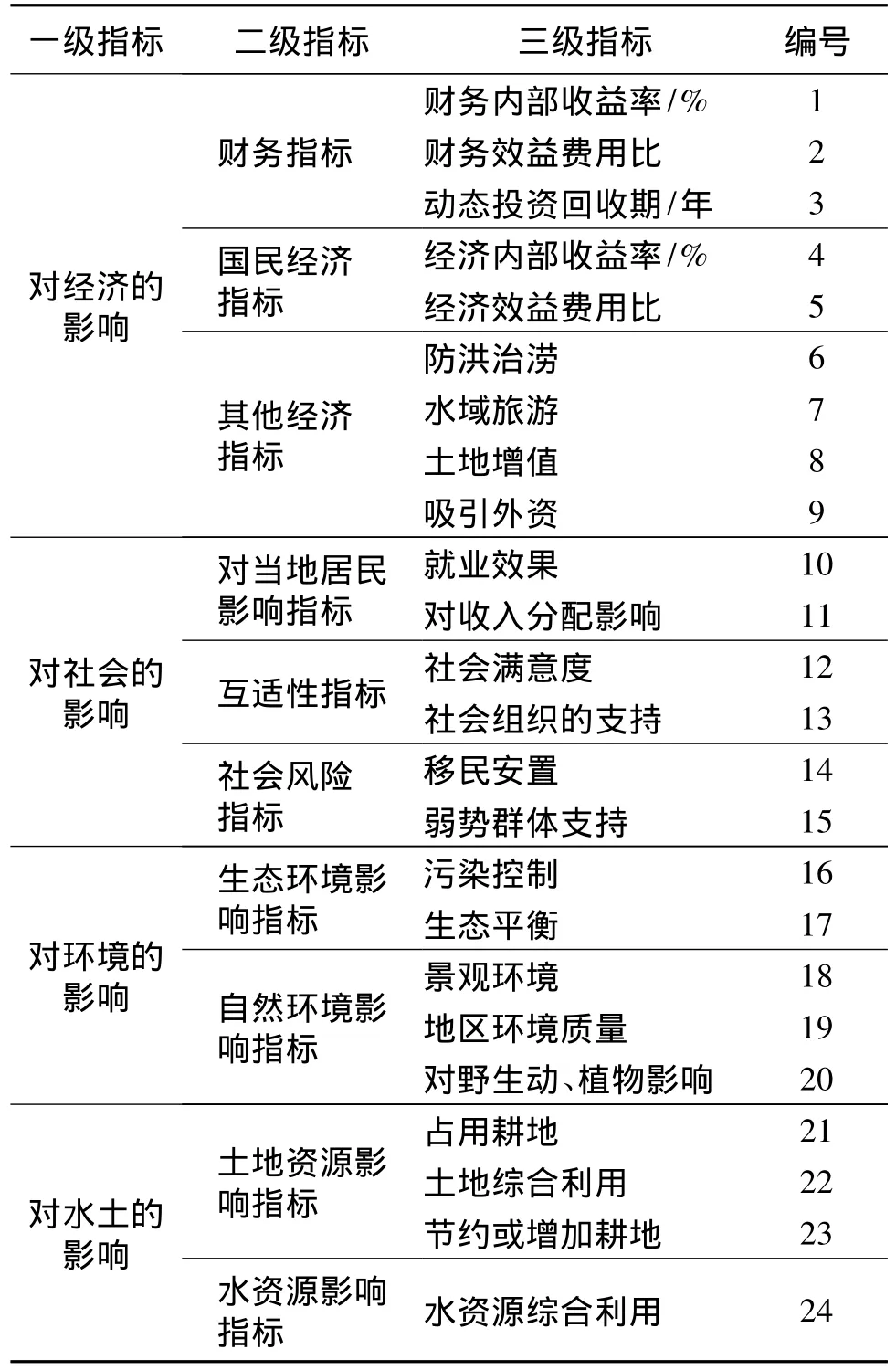
表1 城市湿地公园建设项目社会环境影响评价指标体系
本文对调查问卷中城市湿地公园建设项目社会环境影响评价指标重要性的打分结果进行了因子分析,并输出结果。首先进行的是KMO测度和巴特利特球体检验(bartlett’s test of sphericity),目的是检验样本数据是否适合作因子分析。
2.1.1 经济影响指标因子分析
KMO分析的结果如表2所示。

表2 经济影响评价指标的KMO测度和巴特利特球体检验结果
表2中显示,KMO样本测度值为0.652,说明该样本数据适合作因子分析;表2中的巴特利特球体检验统计值的显著性概率是0.000,小于1%,说明数据相关矩阵间有共同因素存在,适宜作因子分析。再次因子分析,得到旋转后的因子负荷矩阵,如表3所示。
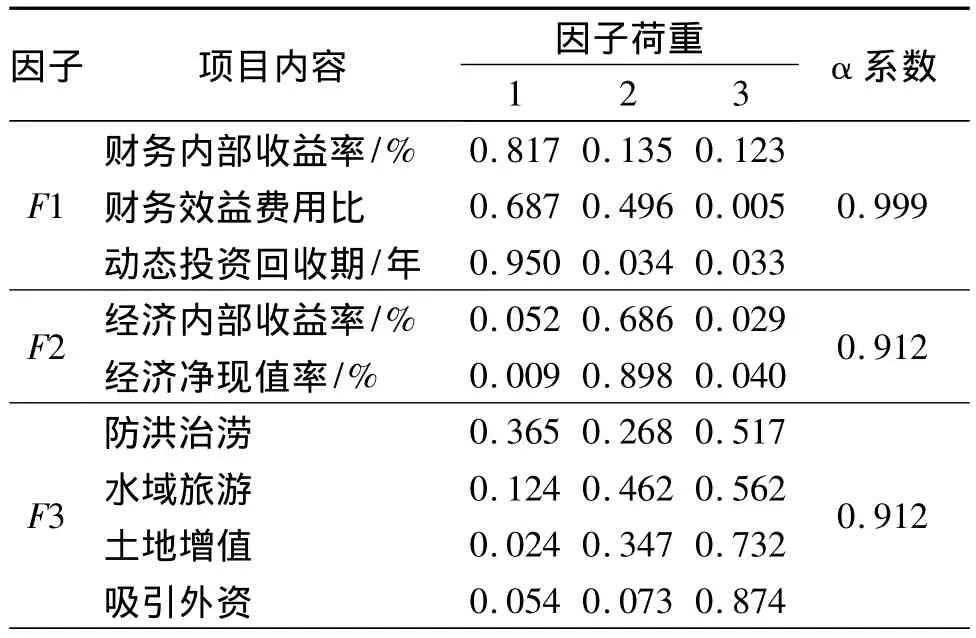
表3 怀仁县城市湿地公园建设项目经济影响评价因子分析
表3的分析显示,怀仁县城市湿地公园建设项目9个经济评价指标被归为3个公因子,它们共同解释了总体方差变异的81.67%,能够比较好地代表原来的9个指标。经过计算,3个因子的Cronbach内部一致性系数(α 系数)分别为0.999、0.912和0.912,说明测量具有较高的一致性程度,而且内部结构良好。
2.1.2 社会影响指标因子分析
KMO分析的结果如表4所示。

表4 社会影响评价指标的KMO测度和巴特利特球体检验结果
表4中显示,KMO样本测度值为0.830,说明该样本数据适合作因子分析;表4中的巴特利特球体检验统计值的显著性概率是0.000,小于1%,说明数据相关矩阵间有共同因素存在,适宜作因子分析。再次因子分析,得到旋转后的因子负荷矩阵,如表5所示。
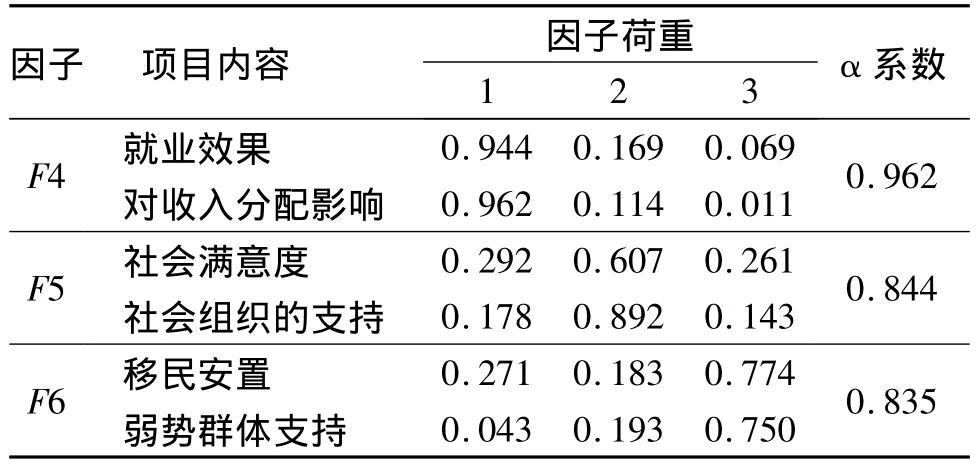
表5 怀仁县城市湿地公园建设项目社会影响评价因子分析
由表5可知,分析结果共产生了3个公因子,它们共同解释了总体方差变异的85.70%,能够比较好地代表原来的6个指标。经过计算,3个因子的Cronbach内部一致性系数(α系数)分别为0.962、0.844和0.835,说明测量具有较高的一致性程度,而且内部结构良好。
2.1.3 环境影响指标因子分析
KMO分析的结果如表6所示。

表6 环境影响评价指标的KMO测度和巴特利特球体检验结果
表6中显示,KMO样本测度值为0.834,说明该样本数据适合作因子分析;表6中的巴特利特球体检验统计值的显著性概率是0.000,小于1%,说明数据相关矩阵间有共同因素存在,适宜作因子分析。再次因子分析,得到旋转后的因子负荷矩阵,如表7所示。
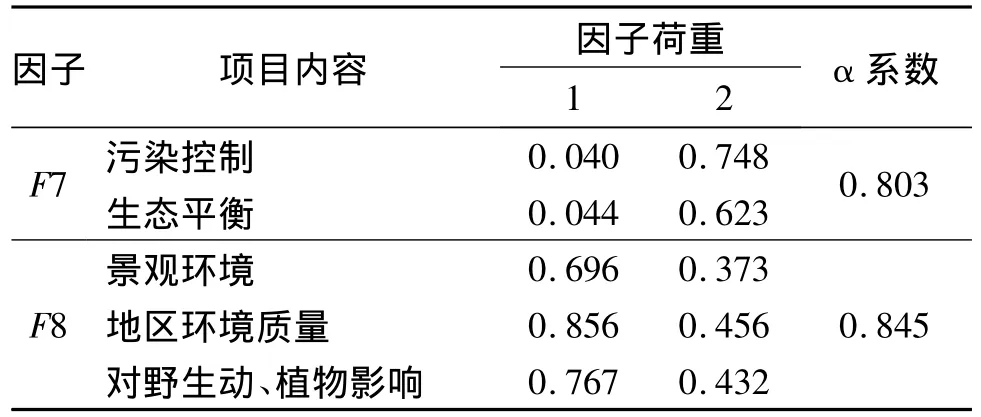
表7 怀仁县城市湿地公园建设项目环境影响评价因子分析
由表7可知,分析结果共产生了2个公因子,它们共同解释了总体方差变异的84.96%,能够比较好地代表原来的5个指标。经过计算,2个因子的Cronbach内部一致性系数(α系数)分别为0.803和0.845,说明测量具有较高的一致性程度,而且内部结构良好。
2.1.4 水土影响指标因子分析
KMO分析的结果如表8所示。

表8 水土影响评价指标的KMO测度和巴特利特球体检验结果
表8中显示,KMO样本测度值为0.560,说明该样本数据适合作因子分析;表8中的巴特利特球体检验统计值的显著性概率是0.000,小于l%,说明数据相关矩阵间有共同因素存在,适宜作因子分析。再次因子分析,得到旋转后的因子负荷矩阵,如表9所示。
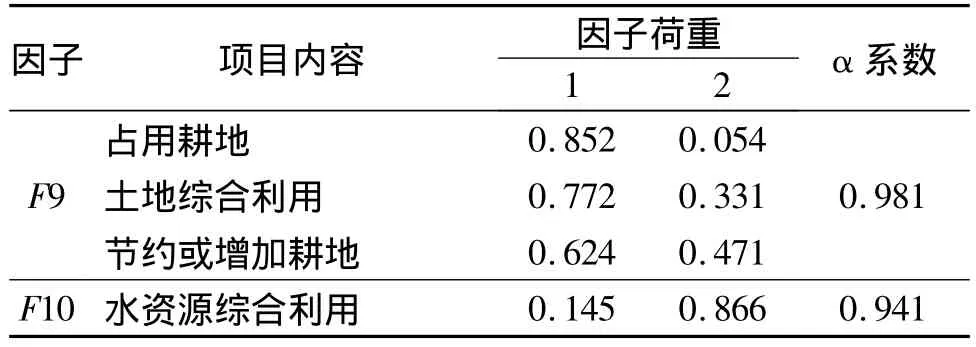
表9 怀仁县城市湿地公园建设项目水土资源影响评价因子分析
由表9可知,分析结果共产生了2个公因子,它们共同解释了总体方差变异的80.41%,能够比较好地代表原来的4个指标。经过计算,2个因子的Cronbach内部一致性系数(α系数)分别为0.981和0.941,说明测量具有较高的一致性程度,而且内部结构良好。
2.1.5 因子分析结果
因子分析对该城市湿地公园建设项目评价指标的概念性模型进行了全面的修正和完善,因子的提取结果在该城市湿地公园建设项目社会环境影响评价指标体系中的结构状态发生了一些变化。从整体上说,概念性模型与实证结果保持了一致性。通过分析,得到城市湿地公园建设项目评价指标体系及其因子荷载和各因子权重,见表10。
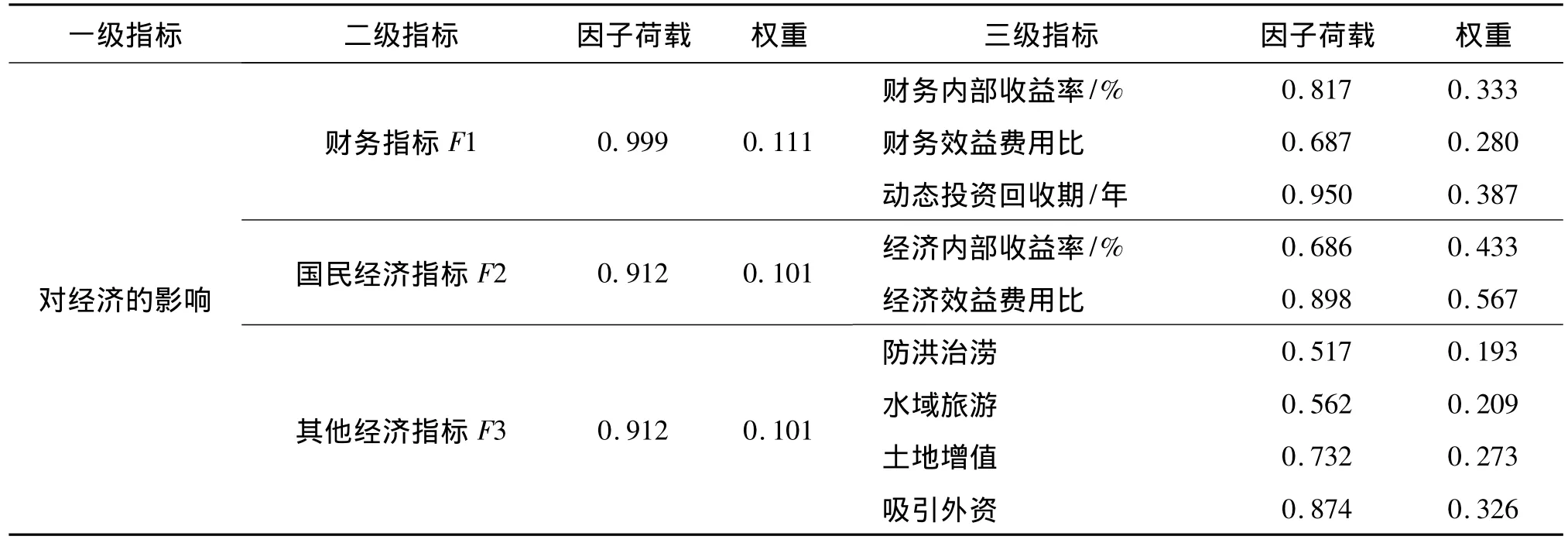
表10 怀仁县城市湿地公园建设项目社会环境影响评价指标体系及其荷载
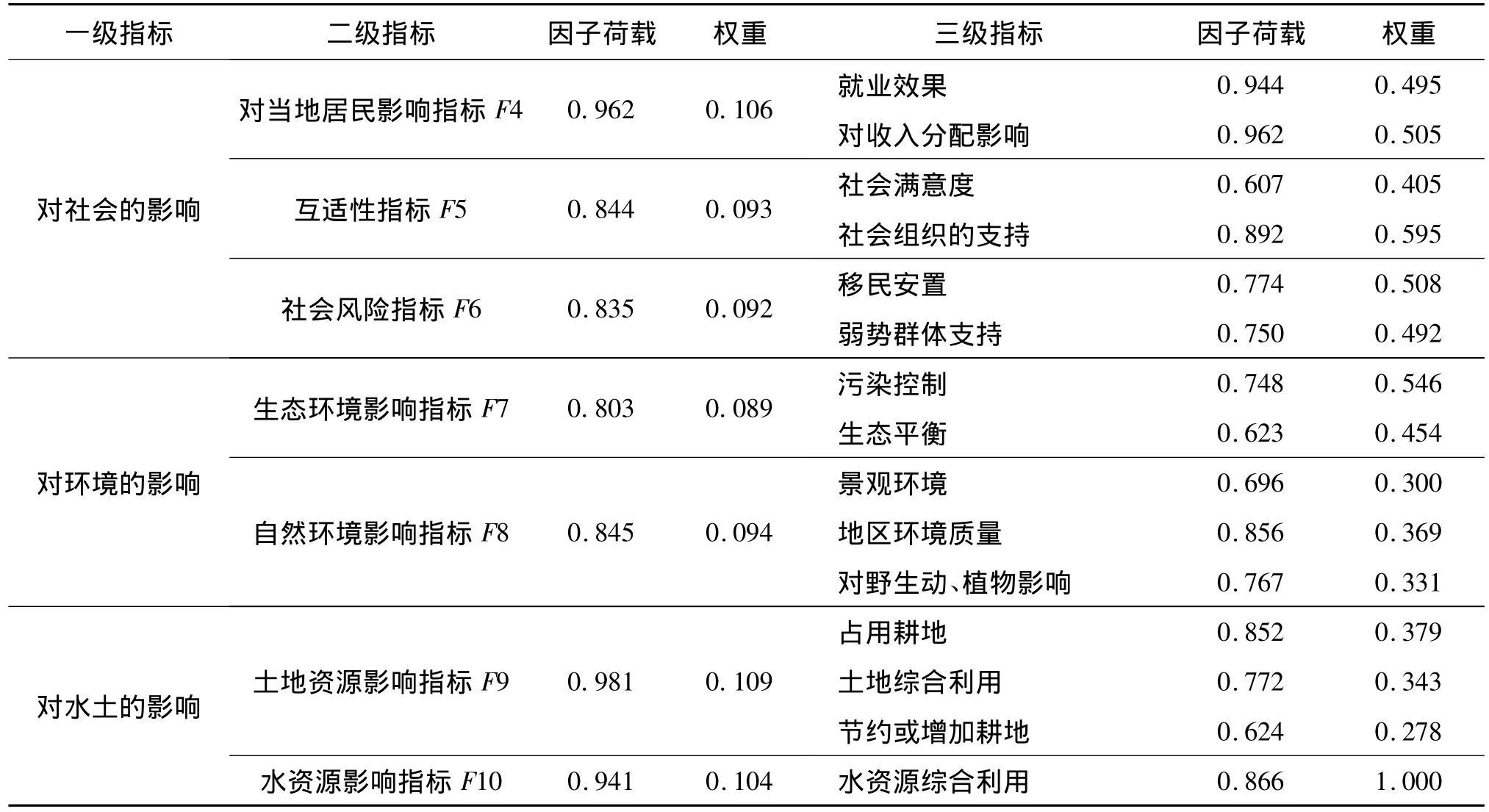
表10 怀仁县城市湿地公园建设项目社会环境影响评价指标体系及其荷载(续表)
2.2 建设项目社会环境影响评价
2.2.1 定量指标评价
通过对该项目分析,得到该项目的各项定量指标数值,如表11。
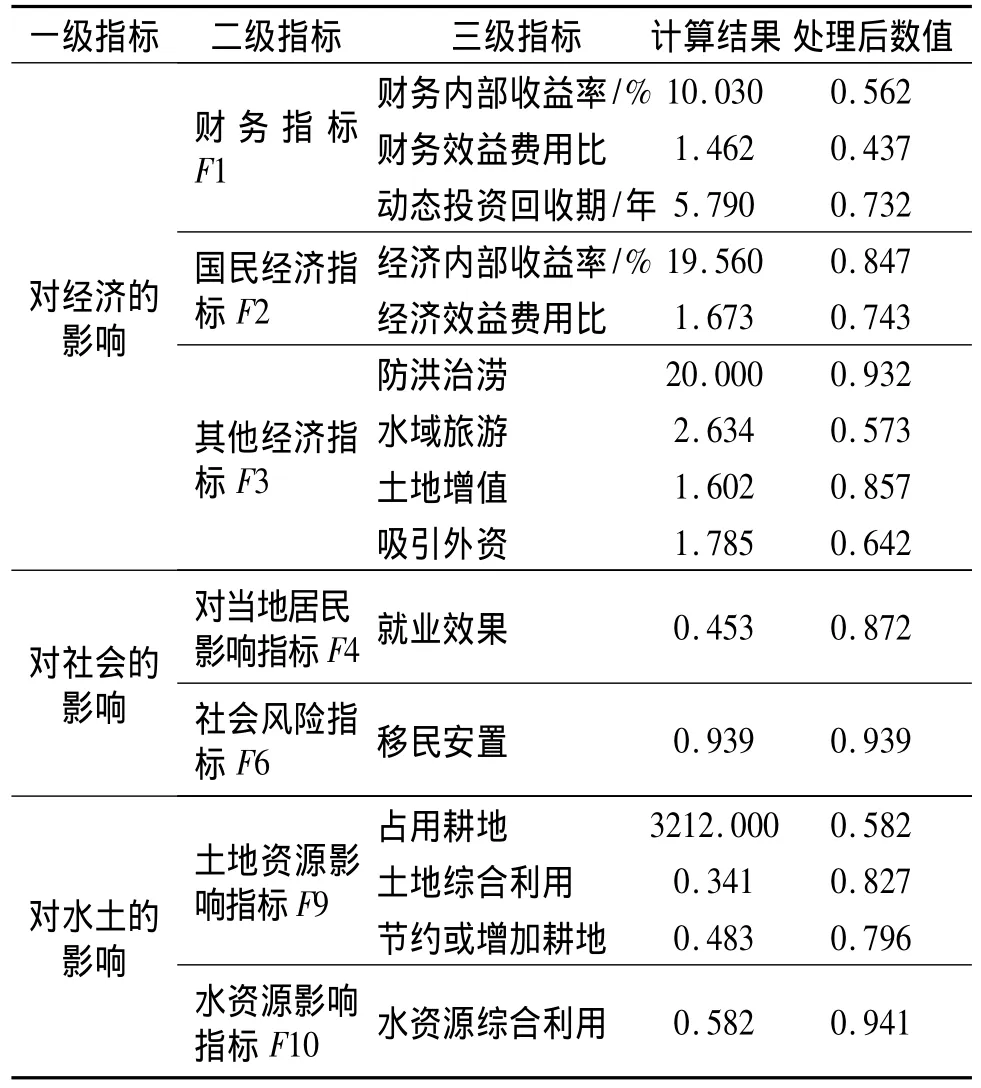
表11 定量指标计算结果
2.2.2 定性指标评价
对定性指标的打分结果进行无量纲化处理,处理结果如表12。
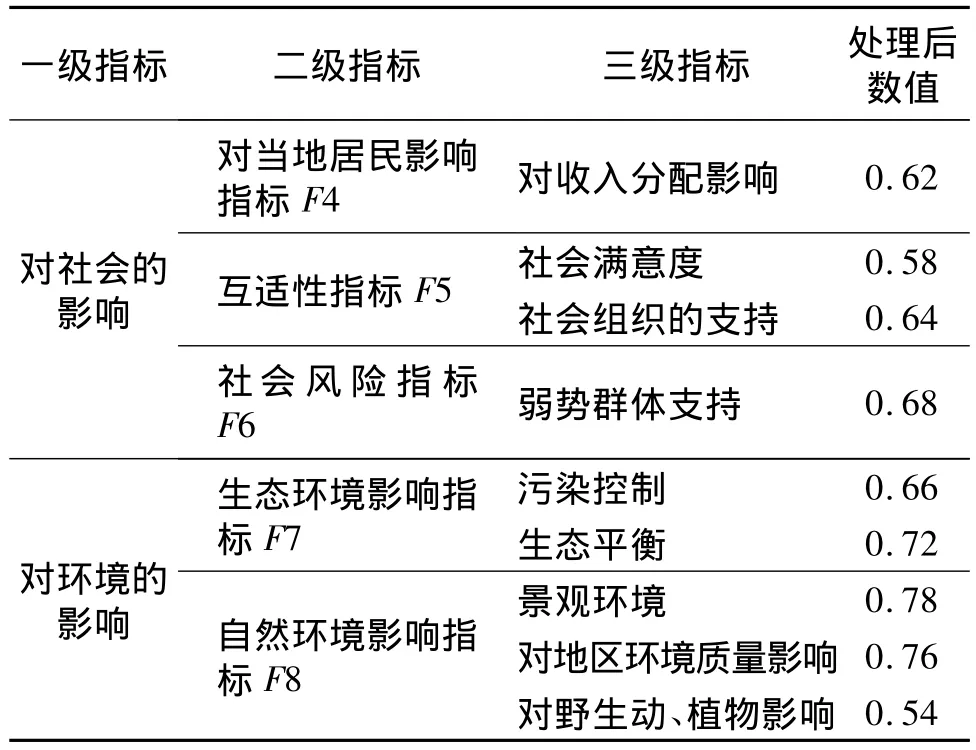
表12 定性指标无量纲化处理结果
2.2.3 怀仁县城市湿地公园建设项目杜会经济效益评价
根据计算结果可以求得该城市湿地公园建设项目主因子得分,如式(1)~式(8)及第54页式(9)~式(11):

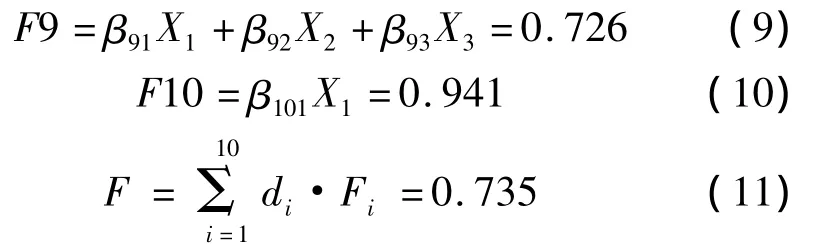
由此得出该城市湿地公园建设项目的社会环境影响评价指标效益的先后顺序是F10>F6>F2>F4>F3>F9>F8>F7>F5>F1。只有水资源影响指标处在 0.80~1.00,为很好;总体评价结果为0.735,处在0.60 ~0.80,为较好。同时可以看出,该项目最薄弱的环节是经济影响中的财务指标。因此,项目应针对评价结果中的薄弱环节给予改善,以保证项目的顺利发展。
3 结论
因子分析法对建设项目社会环境影响评价指标进行检验,既可以避免指标的相关性,又可以克服指标确定的主观性。从众多指标中提取出少量的不相关指标,将构成指标体系的众多原始指标所载信息浓缩并转存到因子中,使原始数据变为可供进一步测评分析的数据基础,再根据方差贡献率确定权重。因此,各综合因子的权重是根据各自的方差贡献率大小来确定的。方差越大的变量越重要,从而具有较大的权重;相反,方差越小的变量所对应的权重也就越小。这就避免了人为确定权重的随意性,使得评价结果唯一,而且较为客观合理。通过对主因子内涵的确定,可以进一步分析出影响建设项目的主要因素,并可以进行有效的决策。
同时,该项目的发展情况与评价结果基本相符。通过怀仁县城市湿地公园建设项目评价案例可以看出,选取指标可以较好地对城市湿地公园建设项目进行评价,并且因子分析模型适用于城市湿地公园建设项目。
[1]李越越.住宅小区环境影响评价中社会环境影响评价内容和方法的探讨[J].2009,4(34):4.
[2]韩勇.水利建设项目后评价中的社会评价研究[D].天津:天津大学建筑工程学院,2005.
[3]王萍.浙扛省水利项目后评价指标体系和方法研究[D].杭州:浙江大学,2006.
[4]朱建平,殷瑞飞.SPSS在统计分析中的应用[M].北京:清华大学出版社,2007:155-170.

