微细电火花加工工具电极夹持用音圈电机结构的优化设计
张明玮,白基成,王燕青
(哈尔滨工业大学机电工程学院,黑龙江哈尔滨 150001)
在用蠕动进给原理[1]进行电极丝损耗补偿的微细电火花加工主轴装置中,微细工具电极夹持模块是重要的组成部分,需要按照一定的控制时序要求对工具电极进行实时夹持及释放;该装置所应用的工具电极夹持音圈电机与普通的电磁驱动器有所不同,对其大出力、体积小型化提出了更高的要求,且该音圈电机能在旋转工况下工作。本课题依据音圈电机新的使用特性要求,首先确定了音圈电机结构方案,并对其出力等特性进行仿真分析,合理确定音圈电机结构方案及最优尺寸。并依据优化设计尺寸试制了新型的音圈电机,实现对微细工具电极的可靠夹持及释放。
1 音圈电机结构形式及比较
根据音圈电机的设计要求,音圈电机需要随主轴一起旋转,故使用轴对称筒形结构,共有轴向充磁式、径向充磁式和聚磁式3 种磁路结构供选择[2],其结构分别见图1~图3。
轴向充磁式和径向充磁式磁路结构是两种传统的磁路结构。轴向充磁工艺简单,成本低;而完整磁环的径向充磁工艺复杂,成本高,所以大多采用瓦型永磁体来代替。径向充磁式音圈电机的磁钢直接和线圈作用,线圈产生变化磁势,可使磁钢产生退磁和充磁。聚磁式结构是一种新的磁路结构,磁漏小,它通过底部轴向充磁的永磁体作用,迫使环形永磁体磁力线向上走,从而在气隙中形成较大的磁感应强度。

图1 轴向充磁式音圈电机结构
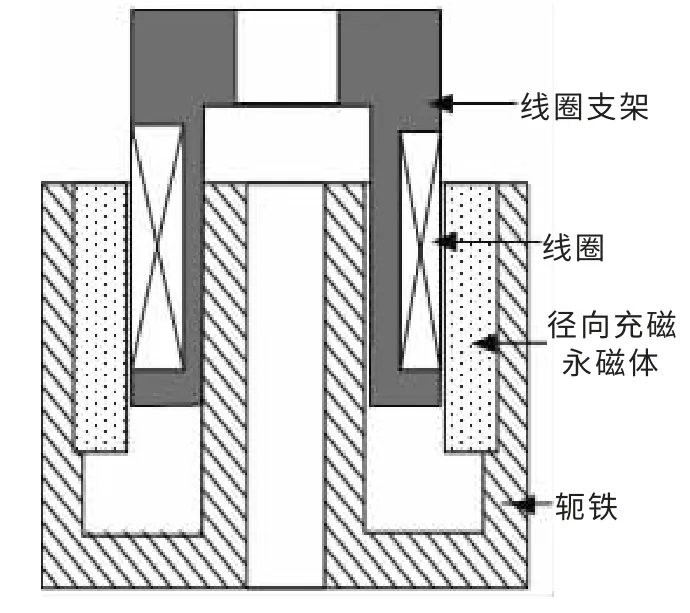
图2 径向充磁式音圈电机结构

图3 聚磁式音圈电机结构
轴向充磁式音圈电机的磁能利用率不高,磁漏较大,气隙中的磁感应强度较小,在同样的永磁体使用量和体积下,输出力明显较小[3]。因此,设计过程主要考虑径向充磁式和聚磁式结构的音圈电机。
采用相同的方法分别分析和设计了聚磁式和径向充磁式两种结构的音圈电机,利用ANSYS 仿真得到聚磁式结构磁场分布云图(图4)和径向充磁式结构磁场分布云图(图5)。
通过对比可发现,聚磁式磁场分布集中于气隙附近,没有磁饱和现象,使磁场能更加均匀有效地作用于线圈。而径向充磁式的磁场集中于左下角,且易产生磁饱和现象,增大磁阻,浪费磁势,与聚磁式相比会消耗更多的永磁体,故选择聚磁式结构进行进一步研究。

图4 聚磁式结构磁场分布云图

图5 径向充磁式结构磁场分布云图
2 新型聚磁式音圈电机
传统的聚磁式结构由轴向充磁磁环、径向充磁磁环和轭铁构成,其性能虽优于轴向充磁式和径向充磁式结构,出力大小也能满足要求,但其出力的平稳性不够好。图6 是由ANSYS 仿真得到的聚磁式结构气隙磁场随轴向位移变化的曲线,很容易看出随着轴向位移的变化,磁场强度变化较大,这将导致电磁力变化大,出力不平稳。

图6 聚磁式结构气隙磁场随轴向位移变化曲线
通过研究发现,在聚磁式结构径向充磁磁环下面加一个非导磁材料制成的隔磁环,将径向磁环与轴向磁环分隔开,这样不仅能减小漏磁,更能使气隙磁场均匀,大大改善出力的平稳性。其结构见图7,气隙磁场随轴向位移的变化见图8。

图7 改进的聚磁式结构图
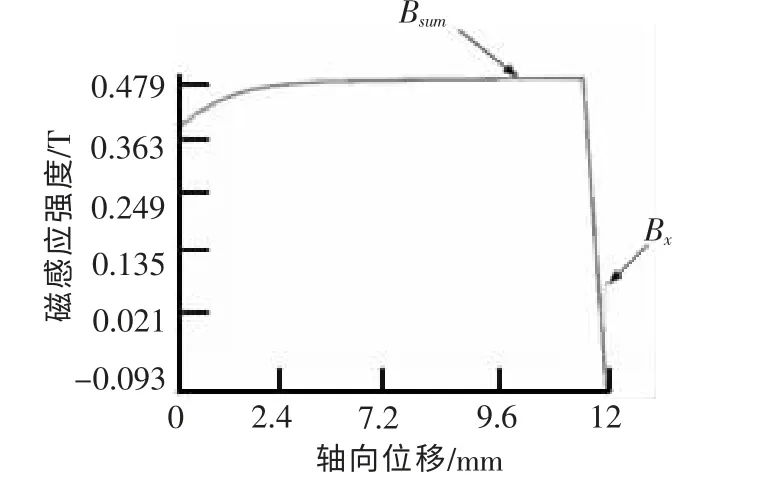
图8 改进的聚磁式结构气隙磁场随轴向位移变化曲线
由图8 可看出,在较长的一段轴向位移内,磁感应强度曲线几乎与X 轴平行,表现出良好的平稳性,故改进后的新型聚磁式结构将工作得更加平稳可靠。
3 音圈电机的优化设计
在确定音圈电机的结构形式后,利用ANSYS对音圈电机进行了优化设计。由于音圈电机不可避免地会有漏磁,所以为了模拟的环境更接近真实情况,在建立的音圈电机模型之外,又建立了3 倍于模型面积的空气模型。因此,磁路系统的几何模型中主要是由永磁体、内外磁轭、线圈支架和气隙组成的一个静态磁场回路,几何上为轴对称结构,故可采用二维模型来代替三维模型。另外,磁路系统是关于Y 轴对称的,所以对磁路的一半建模即可。
对二维静态磁场进行分析,网格划分时采用PLANE53 单元,为四边形八节点单元。受力线圈所在气隙处的磁场分布和永磁体的工作点是我们所关心的,为了计算精确,网格要细化,单元边长为0.5 mm;其他部分根据磁场强度的大小由密到疏划分网格。
设计音圈电机时,应保证有足够的作用力,并兼顾最大磁感应强度、长度和高度等。在优化初始过程中发现,优化结果使气隙面积变得很大,有效线圈长度也变得很大,而磁感应强度变得较小,这样,音圈电机虽然作用力很大,但线圈质量也很大,磁能利用率很低,发热严重。因此,需对气隙中的磁感应强度进行限制。另外,所用的永磁体材料钕铁硼价格较贵,为节省成本,且满足作用力的要求,优化以永磁体体积为目标函数。
最大磁感应强度、直径、高度、气隙中的磁感应强度、力常数BL 都是较重要的物理量,它们的大小需满足设计要求,因而将这些量设为状态变量(表1)。尺寸tqx、dqx、dycn、tycn、dycw、djn、txw等是会影响到永磁体大小、轭铁漏磁程度及音圈电机尺寸大小的结构参数,故将其设为设计变量(表2)。

表1 状态变量及其范围

表2 设计变量及其范围
优化方法可选用零阶算法或一阶算法。本课题所涉及的模型不是很复杂,所以为了提高运算精度,在机时允许的情况下,采用一阶算法进行优化。经圆整的优化结果见表3,其各项指标见表4。

表3 设计变量圆整结果

表4 优化后音圈电机的各项指标
该优化结果使永磁体体积有了较大幅度的减小,高度也较小,力常数和最大磁感应强度均满足要求。
4 不同计算方法的计算结果对比
计算音圈电机产生的电磁力可用洛伦兹力法或有限元法获得。洛伦兹力法是通过仿真得到气隙磁场的磁感应强度后,认为气隙中磁感应强度处处相等,再利用公式F=BIL 进行计算,得到输出力。
有限元法通常包括虚功法和麦克斯韦张量法2种方法计算电磁力。虚功法是基于能量守恒原理和虚位移原理的一种计算方法[4]。麦克斯韦张量法是利用等效的磁张力代替体积力来计算电磁力的方法[5]。两种方法都能在ANSYS 中实现。
音圈电机中的力常数是通过洛伦兹力法计算获得。为验证力常数的正确性,再用有限元法计算。优化结果中,气隙长为14 mm,宽为6 mm,设计电机行程为3 mm,再加上2 mm 的支架宽度和余量,线圈长9 mm,同理减去宽方向的间隙和支架厚度,线圈宽为4.5 mm,则线圈匝数为200 匝,通入电流为1 A,则安匝数F 为200 A。将此磁势加载在线圈上,计算其输出力,结果见表5。可看出,有限元法计算结果和洛伦兹力法计算结果较接近,验证了计算的正确性,同时也说明气隙中磁场分布的均匀性。

表5 输出力计算结果的比较N
电机的输出力随轴向位移不同而变化,会对控制、稳定性等产生不利影响,故有必要研究设计的音圈电机输出力的变化。对线圈施加1.254 A 的电流,研究不同轴向位移对输出力的影响,其结果见图9。可看出,输出力随轴向位移不同而出力均匀,在3 mm 的量程内,最大变化为0.8 N。

图9 输出力随轴向位移的变化
5 样机研制与性能测试
根据仿真计算结果制造出音圈电机,永磁体材料选择钕铁硼N35,磁轭材料选择工业纯铁DT4A,线圈支架材料选择硬铝,线圈为直径0.45 mm的漆包线。音圈电机样机的实物照片见图10,对音圈电机进行出力测试的实验装置见图11。

图10 样机实物照片
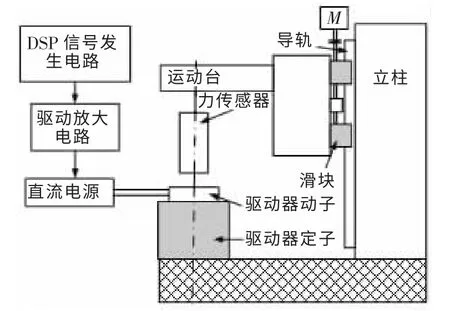
图11 实验装置图
实验过程中,实际测得5 组数据(表6)。求出力常数的平均值为13.888 N/A,理论值为15.86 N/A,两者相差1.972 N/A。此外,通过测量也得到了力常数随动子位移的变化规律(图12)。

表6 力常数测量实验数据

图12 力常数随动子轴向位移的变化
6 结论
本文的重点在对应用于蠕动进给主轴的微细工具电极夹持用音圈电机进行优化设计,以达到尽量减小其体积、增大其出力的指标。分析和优化工作基于ANSYS 有限元分析和优化模块来进行。优化设计完成后,进行加工和出力测试,验证了优化结果的正确性。
[1]毛利尚武.放电加工技术の最近の展开[J].机械と工具,1993(6).
[2]张大卫,冯晓梅.音圈电机的技术原理[J].中北大学学报,2006,27(3):224-228.
[3]沈海涛.动圈型直线压缩机原理性样机的优化与设计[D].杭州:浙江大学,2006.
[4]戴魏,余海涛,胡敏强.基于虚功法的直线同步电机电磁力计算[J].中国电机工程学报,2006,26(22):110-114.
[5]张二攀,石卡.利用麦克斯韦张量法分析永磁电机齿槽转矩[J].微特电机,2010(12):27-30.

