车辆多体系统振动方程建立探讨

全顺喜，王 平，赵才友

(1.中铁第四勘察设计院集团有限公司，武汉 430063;2.西南交通大学 高速铁路线路工程教育部重点实验室，成都 610031)

进行车辆-轨道耦合动力学研究时，需先建立车辆-轨道耦合系统振动方程。通常将车辆模拟成由车体、转向架、轮对组成的多刚体子系统，将轨道模拟成由梁、质量块等组成的子系统，分别建立振动方程，并通过复杂轮轨接触实现两子系统动态耦合［1］。建立车辆多体系统振动方程常用方法有三种:①利用达朗贝尔原理直接平衡法［2］，该法对简单问题较直接、方便，但对自由度多的车辆系统须先对车辆各部件受力详细分析后依次写出各刚体运动方程。②矩阵组装法［3-4］，该法虽可利用计算机自动形成车辆振动方程，但须先手工推导出各类变换矩阵。③能量法，如哈密尔顿原理、拉格朗日方程、势能驻值原理等［5-8］，该法从功、能角度建立系统振动方程，较适用于难直接写出力平衡方程的复杂结构，而哈密尔顿原理因只含纯粹标量，较方便应用。

用哈密尔顿与势能驻值原理时，需用“对号入座”法则建立系统振动方程［8-10］。但目前该法则尚未用有限元法中计算机编码法，不能将单元矩阵自动组建成总体矩阵。为此，文献［11］采用有限单元法建立车辆多体系统振动方程。而本文对“对号入座”法则进行改进，使之与有限元分析中计算机编码法统一，快速利用计算机将单元矩阵自动建成系统总体矩阵，方便了应用哈密尔顿原理建立车辆多体系统振动方程过程。

1 哈密尔顿原理与改进的“对号入座”法则

1.1 哈密尔顿原理简介［8］

据哈密尔顿原理提供的准则，利用动能、势能等标量可将实际发生的运动从可能发生的(约束所许可的)运动中挑选出来。哈密尔顿原理表达式为:

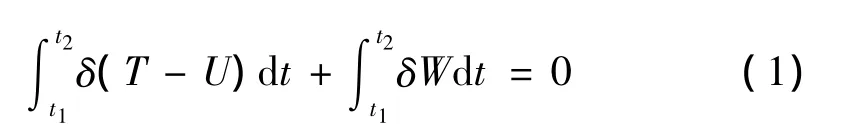
式中:T为系统总动能;U为系统总势能;δ为变分或虚位移符号;δW为保守力及非保守力所做虚功总和;t1，t2为积分起止时间。式(1)表示在任何时间段内，系统总动能与总势能之差的变分加保守力与非保守力所做功的变分等于零。应用此原理，可方便地据系统总动能、总势能及相应的虚功直接导出运动方程。

1.2 应用哈密尔顿原理建立振动方程

以图1振动系统为例。其中m1～m3分别为三参振体质量;k1～k3分别为三弹簧刚度值;c1～c3分别为三阻尼器阻尼值;z1～z3分别为三参振动体振动位移，向下为正;P(t)为作用于系统随时间变化外荷载。三自由度振动系统总动能一阶变分表达式为:

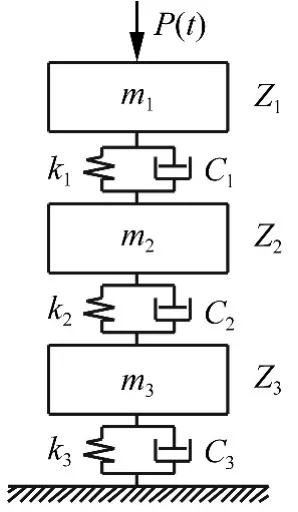
图1 振动系统Fig.1 Vibration system

由式(1)关于系统总动能积分形式，利用逐步积分得:

据“对号入座”法则，将与加速度对应项放入总质量矩阵中，其对应系统质量矩阵［M］可由式(3)加速度与变分角标获得，即:

系统总势能一阶变分式为:

为利用“对号入座”法则，将式(5)改写成位移与变分相乘形式，即:

将与位移对应项放入总刚度矩阵中，其对应系统刚度矩阵［K］可由式(6)中位移与变分角标获得，即:

同理可得系统阻尼力所做虚功，利用“对号入座”法则，将之改写成速度与变分相乘形式，即:

将与速度对应项放入总阻尼矩阵，其对应系统阻尼矩阵［C］可由式(8)中速度与变分角标获得，即:

外荷载所做虚功δW2=δz1P(t)对应系统的外荷载列阵［Q］，即:

至此，系统总动能、总势能变分及阻尼力、外力所做虚功均已求出，令 {q}=［z1z2z3］T、{δq}=［δz1δz2δz3］，利用哈密尔顿原理得:

由于{δq}的任意性，须式(11)括号内表达式为零时方可满足，由此得系统振动方程为:

1.3 “对号入座”法则改进

由以上推导知，在利用“对号入座”法则获取系统质量、刚度、阻尼及荷载矩阵时，需先将系统总动能、总势能、阻尼及外力所做虚功写成加速度与变分、位移与变分、速度与变分、外力与变分相乘形式，再据其角标将各项分别放入对应的质量、刚度、阻尼、荷载矩阵中，而未利用有限元法中用计算机将单元矩阵自动组成总体矩阵优势。系统自由度较多时，此过程仍较繁琐。为此，本文对其进行改进，将式(3)、式(5)、式(8)及外力所做虚功写成矩阵形式，再将各参振质量块、弹簧、阻尼及外力对应的矩阵分别合并获取系统总质量、总刚度、总阻尼、总荷载矩阵。以形成系统总刚度矩阵为例，将式(5)改写成矩阵形式为:

式中:K1，K2，K3分别为弹簧k1，k2，k3对应的刚度矩阵，由式(5)直接得出为:k1［-1，1］T［-1，1］、k2［-1，1］T［-1，1］、k3［0，1］T［0，1］。将弹簧k1，k2，k3对应的刚度矩阵合并即得系统总刚度矩阵，即:

系统总质量、总阻尼、总荷载矩阵均可按该方法获取。由此，① 该方法中各参振质量块、弹簧、阻尼、外力对应的子矩阵较易写出，且具有类似性，方便计算机输入;② 系统自由度较多时，通过改进后方法能借鉴有限元分析思想，可据编好的各参振质量块、弹簧、阻尼、外力对应的子矩阵在总质量、总刚度、总阻尼矩阵中序号，利用计算机将子矩阵自动组成系统总体矩阵。极大方便了自由度多的车辆多体系统振动方程建立。

2 建立全车-轨道垂向耦合振动方程

2.1 全车-轨道垂向振动模型

为建立全车-轨道垂向耦合振动方程，先建立该系统振动模型，见图2。该模型中车辆子系统由一个车体、两个转向架、四个轮对共七个刚体及一、二系悬挂组成。对车体及转向架考虑沉浮、侧滚、点头3个自由度，对轮对考虑沉浮、侧滚2个自由度，整个车辆子系统共17个自由度。轨道子系统包括以欧拉梁模拟的钢轨、轨枕、以弹簧阻尼装置模拟的扣件、道床，且钢轨采用弹性点支承模型，轨枕采用连续支承模型，并用有限单元法进行离散。

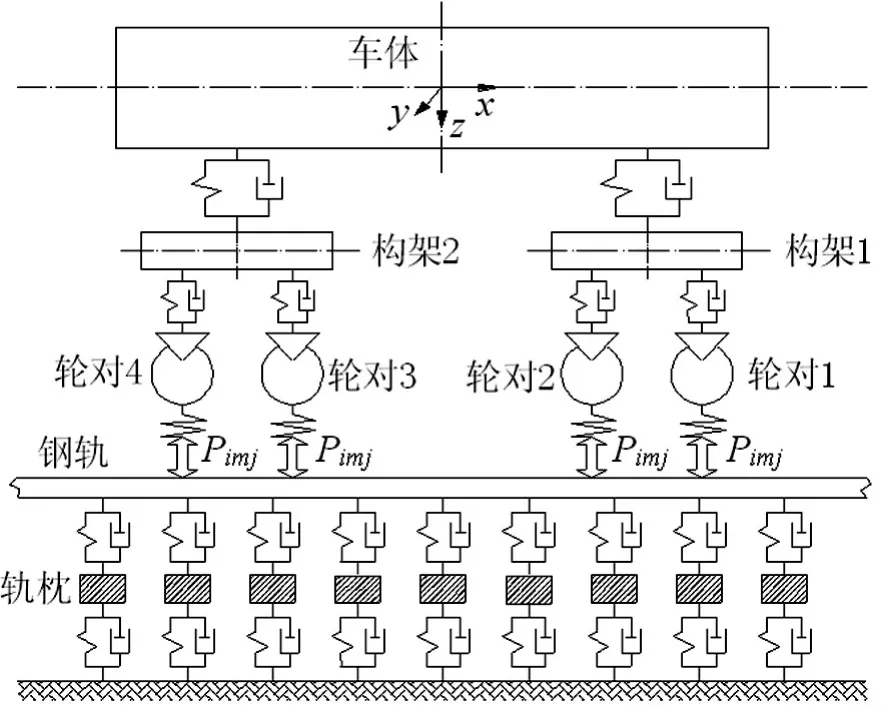
图2 全车-轨道垂向振动模型Fig.2 Vertical model for vehicle-track coupling system

2.2 全车-轨道垂向耦合振动方程建立

由图2容易获得车辆子系统总动能，考虑到哈密尔顿原理中关于系统总动能积分形式，将其逐步积分得:

车辆子系统总势能为:

令二系悬挂连接的车体、转向架位移{qcti}=［zc，φc，βc，zti，φti，βti］T、变分{δqcti}=［δzc，δφc，δβc，δzti，δφti，δβti］;一系悬挂连接的转向架、轮对位移{qtwim}=［zti，φti，βti，zwim，φwim］、变分{δqtwim}= ［δzti，δφti，δβti，δzwim，δφwim］。利用改进后的“对号入座”法则，式(16)一阶变分写为:

式(15)～式(17)中:i表示车体下有两个转向架;m表示转向架下有两个轮对;j=1表示左侧悬挂，j=2表示右侧悬挂;mc，Icx，Icy为车体质量、侧滚、点头转动惯量;mt，Itx，Ity为转向架质量、侧滚、点头转动惯量;mw，Iwx为轮对质量、侧滚转动惯量;zc，φc，βc表示车体沉浮、侧股、点头;zti，φti，βti表示转向架沉浮、侧股、点头;zwim，φwim表示轮对沉浮、侧股;Lc，Lt，d1，d2表示一、二系悬挂纵向距离及横向距离之半;k1z，k2z，{K1zimj}，{K2zij}分别为一、二系悬挂垂向刚度及其刚度子矩阵，由式(16)可得{K1zimj}=k1z［1，(-1)jd1，(-1)mLt， -1，(-1)j+1d1］T［1，(-1)jd1，(-1)mLt，-1，(-1)j+1d1］，{K2zij}=k2z［1，(-1)jd2，(-1)iLc，-1，(-1)j+1d2，0］T［1，(-1)jd2，(-1)iLc，-1，(-1)j+1d2，0］。

车辆子系统中阻尼力所做虚功为:

为利用改进后“对号入座”，将式(18)改写为:

式中:c1z，c2z，{C1zimj}，{C2zij}分别为一、二系悬挂的垂向阻尼及其阻尼子矩阵，由式(18)可得{C1zimj}={K1zimj}c1z/k1z，{C2zij}={K2zij}c2z/k2z。

轮轨垂向力对车辆子系统所做虚功为:

式中:Pimj为轮对左右侧轮轨垂向力，向下为正。同理，也可将式(20)写成荷载子列阵形式。

由式(15)、式(17)、式(19)、式(20)，据哈密尔顿原理，用以上组建总质量、总刚度、总阻尼、总荷载矩阵方法，利用计算机自动组建车辆系统振动方程，即:

式中:［M］c，［C］c，［K］c，{Pc}为车辆子系统总质量、总阻尼、总刚度、总荷载矩阵;{uc}为车辆系统位移矩阵。对轨道子系统，可用有限单元法建立振动方程［8］。

2.3 振动方程求解

车辆、轨道子系统是相互作用、密不可分的两个部分，主要通过轮轨间作用力相互联系。对求轮轨间作用力而言，文献［1］采用新型积分方法［12-13］求解系统振动方程，该方法中下一时刻位移列阵只与本时刻位移、速度、加速度列阵及上一时刻加速度列阵有关，下一时刻轮轨作用力可据本时刻及上一时刻振动响应求出，勿需迭代求解;文献［8-14］采用Park法求解系统振动方程组，而据Park法，下一时刻位移列阵不但与本时刻及上一时刻位移、速度、加速度列阵有关，且与下一时刻荷载列向量即轮轨作用力有关，因此，下一时刻轮轨作用力需反复迭代，对轮轨间垂向力，可采用牛顿迭代法求解。

由于本文用有限单元法离散轨道子系统，其质量矩阵非对角阵，即不能用新型积分方法求解振动方程。故采用Park法求解全车-轨道垂向耦合振动方程。考虑到用牛顿迭代法求解轮轨垂向力时要写出迭代雅克比阵，计算较复杂，且在车辆-轨道空间耦合振动分析中，轮轨间法向力不但与轮对垂向位移、轮对侧滚角、钢轨垂向位移、垂向不平顺有关，且与轮对横向位移、轮对摇头角、钢轨横向位移、车轮踏面、轮下钢轨轮廓等有关，该迭代雅克比阵无法写出。因此先将非线性赫兹弹簧简化成线性弹簧，采用直接迭代法求解轮轨垂向力。

设车辆静轮重P0，轮轨间接触等效线性刚度为［15］:

式中:G为轮轨接触常数，踏面为锥形时，G=4.57R-0.149×10-8;踏面为磨耗型时，G=4.57R-0.149×10-8(R为车轮半径)。数值试验表明，积分步长小于0.2 ms时，迭代过程收敛，约迭代5次即可满足1%精度要求。

据全车-轨道垂向振动模型及求解方法，用MATLAB编制的计算程序，可用于各种条件下全车-轨道垂向耦合振动分析。

3 焊接凹接头激励下车辆-轨道垂向振动特性

3.1 计算参数

为验证建立车辆多体系统振动方程方法的正确性，对焊接凹接头激励下车辆-轨道垂向振动特性进行分析。采用CRH3型动车组、CHN60钢轨，弹性模量E=2.1 ×105MPa，热膨胀系数 α =1.18 ×10-5，泊松比0.3，扣件间距0.625 m。轨道子系统相关参数见表1。

钢轨焊接凹接头可用两波长与幅值不同的余弦波叠加表示，取两余弦波波长分别为1 m、0.1 m，幅值分别为0.2 mm，0.1 mm，如图3 所示［16］。

图3 钢轨焊接凹接头不平顺Fig.3 Track irregularities of welded concave joints

3.2 计算结果

车辆以250 km/h通过焊接凹接头时，车辆-轨道垂向振动响应如图4所示。

由图4看出，焊接凹接头对车辆-轨道垂向振动特性影响较大。车辆进入焊接凹接头区域时，凹接头侧轮轨垂向力迅速减载至28.5 kN，随后又增大到117.3 kN，约为静轮载的1.7倍，而非凹接头侧轮轨垂向力波动较小;车体垂向加速度存在两个明显波动区，由车辆前后转向架通过焊接凹接头时所致，但由于车辆悬挂系统隔振效果，波动幅值较小，最大值不超过0.04 m/s2;车辆通过时，焊接凹接头附近钢轨、轨枕加速度、位移较大，加速度最大值分别为1 496 m/s2、127 m/s2，位移最大值分别为 0.77 mm、0.23 mm，比无不平顺时增加许多，会影响钢轨使用寿命。本文计算结果在波形上或量值上均与文献［16］结果接近，说明本文所提建立车辆多体系统振动方程方法正确、可行。

图4 焊接凹接头不平顺下系统振动响应Fig.4 Vibration responses of the vehicle-track coupling system under the welded concave joints irregularity

4 结论

为方便应用哈密尔顿原理建立车辆多体系统振动方程，本文工作为:

(1)以三自由度振动系统为例，对哈密尔顿原理“对号入座”进行改进，使之与有限元分析中计算机编码法统一，快速利用计算机将单元矩阵自动组成系统总体矩阵。

(2)建立全车-轨道垂向振动模型，应用改进后“对号入座”法则建立该振动系统方程，并应用MATLAB编制相应计算程序。

(3)用所编程序对焊接凹接头激励下车辆-轨道垂向振动特性进行分析，结果表明，本文计算结果与之前研究结论较一致，表明本文所提方法的正确性。

［1］翟婉明.车辆-轨道耦合动力学(第三版)［M］.北京:科学出版社，2007.

［2］翟婉明.车辆-轨道垂向系统的统一模型及其耦合动力学原理［J］.铁道学报，1992，14(3):10-21.

ZHAI Wan-ming.The vertical model of vehicle-track system and its coupling dynamics［J］.Journal of The China Railway Society，1992，14(3):10-21.

［3］张定贤.机车车辆轨道系统动力学［M］.北京:中国铁道出版社，1996.

［4］倪纯双，洪嘉振，贺启庸.车辆系统动力学的符号化多体方法［J］.中国铁道科学，1996，17(4):12-17.

NI Chun-shuang，HONG Jia-zhen，HE Qi-yong.Symbolic multibody approach of vehicle system dynamics［J］.China Railway Science，1996，17(4):12-17.

［5］曾庆元.弹性系统动力学总势能不变值原理［J］.华中理工大学学报，2000，28(1):1-3.

ZENG Qing-yuan.The principle of total potential energy with stationary value in elastic system dynamics［J］.Journal of Huazhong University of Science and Technology，2000，28(1):1-3.

［6］曾庆元.弹性系统动力学总势能不变值原理与列车桥梁时变系统振动分析［J］.铁道建筑技术，2001(1):1-6.

ZENG Qing-yuan.The principle of total potential energy with stationary value in elastic system dynamics and the vibration analysis of hain-bridge time-varying system［J］.Railway Construction Technology，2001(1):1-6.

［7］张亚辉，林家浩.结构动力学基础［M］.大连:大连理工大学出版社，2007.

［8］刘学毅，王 平.车辆-轨道-路基系统动力学［M］.成都:西南交通大学出版社，2010.

［9］曾庆元，杨 平.形成矩阵的“对号入座”法则与桁梁空间分析的桁段有限元法［J］.铁道学报，1986，8(2):48-59.

ZENG Qing-yuan，YANG Ping.The"set-in-right-position"rule for forming structural matrices and the finite trusselement method for space analysis of truss bridges［J］.Journal of The China Railway Society，1986，8(2):48-59.

［10］向 俊，曾庆元.关于机车车辆-轨道系统运动方程的建立［J］.长沙铁道学院学报，2000，18(4):1-5.

XIANG Jun，ZENG Qing-yuan.On building equations of motion of locomotive vehicle-track system［J］.Journal of Changsha Railway University，2000，18(4):1-5.

［11］李东平，曾庆元，娄 平.车辆多体系统动力学方程的有限元法［J］.中国铁道科学，2004，25(5):33-38.

LI Dong-ping，ZENG Qing-yuan，LOU Ping.The finite element method forestablishingdynamicalequationsof vehicle multi-body system［J］.China Railway Science，2004，25(5):33-38.

［12］翟婉明.非线性结构动力分析的Newmark预测-校正积分模式［J］.计算结构力学及其应用，1990，7(2):51-58.

ZHAI Wan-ming.The predictor-corrector scheme based on the newmarks integration algorithm for nonlinear structural dynamic analyses［J］.Chinese Journal of Computational Mechanics，1990，7(2):51-58.

［13］Zhai W M.Two simple fast integration methods for large-scale dynamic problems in engineering［J］.International Journal for Numerical Methods in Engineering，1996，39(24):4199-4214.

［14］王 平.道岔区轮轨系统动力学的研究［D］.成都:西南交通大学，1998.

［15］李成辉，万复光.轨道结构随机振动［J］.铁道学报，1998(3):97-101.

LI Cheng-hui，WAN Fu-guang.Random vibration of track structure［J］. Journal of The China Railway Society，1998(3):97-101.

［16］王伟华.土路基上双块式无砟轨道垂向动力特性分析［D］.成都:西南交通大学，2009.