基于同伦迭代算法的弱耦合梁损伤识别
雷晓光,吕中荣,刘济科
(中山大学 力学系,广州 510006)
工程结构长期处于各种复杂工作环境中并不断使用及损耗,总会出现各种损伤,而微小损伤一旦未被及时发现,损伤的积累会给整个结构带来灾难性后果。因此早期损伤识别[1]对保障结构安全非常重要。
大多据结构响应对物理参数变化提出的检测方法,均在频域[2-5]内进行。而实际工程中,大量结构由于自身对称性常会出现重频[6]或近似重频的退化系统。如海洋石油平台、飞机、多跨连续梁结构等。在此种情况下,频域损伤识别方法难以保证获得收敛的识别结果。因此研究重频损伤识别问题意义重大。
本文在时域内对具有重频特性的耦合结构进行损伤识别,以系统抗弯刚度参数作为损伤识别指标,引入同伦迭代法[7]对结构损伤进行定位及程度确定。利用有限元计算响应与模拟测量响应最小化获得非线性目标函数,对目标函数对各损伤参数求偏导获得时域内的识别方程。采用最小二乘法构造同伦方程[7]进行迭代求解,其实质是在时域内非线性大范围收敛识别方法。其收敛不依赖于初始值选择,且可对具有重频的多跨结构进行准确识别。利用车辆经过多跨桥梁时产生的加速度响应检测结构损伤。以两跨弱耦合连续梁为例,通过数值算例中对单一局部损伤及多个局部损伤工况分别进行识别,进一步讨论噪声对识别结果影响,仿真算例表明本文方法在有噪声环境下能较准确识别具有相重频率的多跨连续梁局部损伤。
1 正问题
1.1 连续梁系统有限元模型
图1为两跨耦合连续梁,通过有限元法离散,系统强迫振动方程可写为:
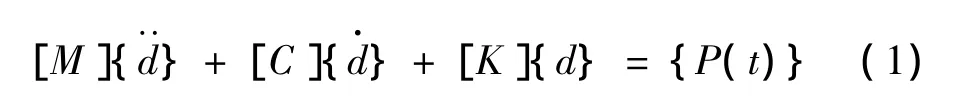
式中:[M],[K],[C]分别为系统质量矩阵、刚度矩阵、阻尼矩阵,本文采用瑞雷阻尼模型:[C]=a1[M]+a2[K],其中常数a1,a2由两个不等的振动模态频率与给定阻尼比率确定,{P(t)}为系统节点力向量。图中1,11为有限元节点编号。

图1 双跨耦合梁系统Fig.1 The coupled beam system
1.2 连续梁系统自由振动频率与强迫振动响应
无阻尼系统自由振动方程可表示为:
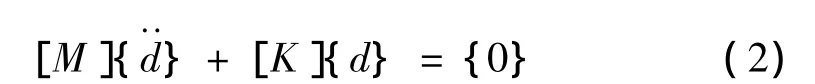
其特征值表达式为:

式中:λi=ω2
i,ωi为第i个模态圆频率;{u}i为第i阶模态振型。外激励力作用下的强迫振动响应可由式(1)求出。本文采用工程中常用的Newmark直接积分法求解。
2 同伦识别法求解
2.1 同伦法基本原理[7]
结构损伤识别问题可归结为问题的逆向优化求解,通过损伤模型获得响应反演系统局部损伤状况。直接利用时域响应数据反推系统结构真实损伤状况。损伤识别问题求解归结为寻找损伤向量x=(x1,x2,…,xn)T,使目标函数J(x)=(w-w*)T(w-w*)/2取得极小值,w*=(w1,w2,…,wn)T为已测得的结构测点响应幅值,即损伤结构真实响应(可以是位移、速度、加速度等)。此处采用结构响应加速度,因其包含的结构损伤信息量较多。w为结构系统计算响应数据。损伤识别问题转化为求解非线性方程组:

同伦法思想是对f(x)=0引入参数t构造一簇映射K,当t为某个特定数值:t=1,K变为式(7)中的f(x),t=0可得方程f0(x)=0的解x0,即构造一簇映射使K满足K(x,0)=f0(x),K(x,1)=f(x),其中f0(x)=0的解x0为已知,即初始迭代值。而方程K(x,1)=f(x)即为原非线性方程组。由此,结构损伤识别问题转化为求同伦方程K(x,t)=0解的问题。其解为x=x(t)。通过引入同伦参数t[0,1],建立同伦方程为:

式中:x0为任意取定初值;f(x)为非线性方程组左边向量函数;t=0,t=1时式(5)变为:
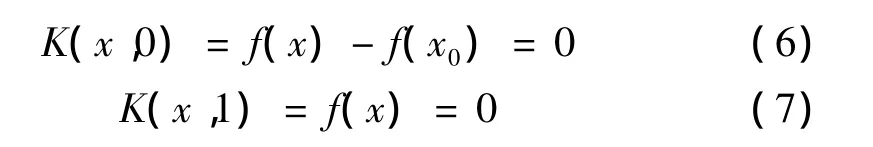
参数t在区间[0,1]变化时,K(x,t)构成一组同伦映射,对应同伦方程(5)的解x=x(t)从而构成空间曲线。曲线一端(t=0)表示f(x)-f(x0)=0的解;另一端(t=1)表示f(x)=0的解。因此只要控制参数t从0到1变化跟踪曲线x=x(t)即能找到原问题的解。K(x,1)=0的每个孤立解至少一条由t=0时曲线跟踪获得,即函数曲线的起点为K(x,0)=0的解。构造的同伦函数有该性质时全部孤立解可通过跟踪同伦函数路径获得。跟踪曲线基本数学方法见文献[7],其基本思想为使同伦方程恒成立:

由于初值x0可任意选取,且在选取过程中未做任何假定,故同伦延拓法亦为大范围收敛的非线性方法,式(5)的求解可采用牛顿迭代法。即将t在[0,1]区间上分为n份记作tr=r/N,(r=0,1,2......N),当r=0时,K(x,t)=K(x,0)=0 的解x(0)=x0已知,取r=0,1,2......N一个解为初始值,用牛顿法迭代公式为:

其中:r=0,1,2,3……,N-1。f'(xr)为计算中待求的雅克比矩阵,相当于灵敏度矩阵[8],表达式为:

K(x,t)=0可以有多种表达形式,如K(x,t)=tf(x)+(1-t)f(x-x0)等形式。同伦方程所取表达式不同,结果及求解速度也不同,本文采用K(x,t)=f(x)+(1-t)f(x0)形式,在计算迭代过程中,同伦参数等分数的划分对计算结果收敛快慢程度影响较大:同伦参数取值较大时,模型对应的雅克比矩阵趋近于奇异矩阵,使计算结果不能收敛。为避免该病态的出现,迭代时给雅克比矩阵增加一正则矩阵aI,I为单位矩阵,a为正则化参数[9],以保证结果收敛。
3 数值算例
3.1 损伤识别
对图1系统用有限元离散为10个均匀欧拉-伯努利梁单元。参数设为:杨氏模量E=3.4 GPa,密度p=2 800 kg/m3,横向耦合弹簧刚度 2.7 ×109N/m,扭转耦合弹簧刚度2.7×107N·m/rad,每跨长10 m,梁横截面积 0.15×0.15 m2,作用于梁系统的外激励P(t)=15 000[1+0.1sin(10πt)]N,计算响应时假定移动力在梁左端以5 m/s速度匀速移动到右端,时间步长0.005 s,进行不同工况下损伤识别。
3.1.1 单一损伤识别
将单元9的刚度折减5%模拟局部小损伤,利用5号节点加速度响应数据进行损伤检测,取前4 s响应数据进行识别。不考虑测量噪声影响,经9次迭代后识别结果见图2。由图2看出,本文方法能成功识别出系统局部损伤。即此方法可用于识别早期微小损伤。
3.1.2 多处损伤识别
设系统第2,3,7号单元刚度分别有2%,3%,5%的减少。移动力加速度响应位置同单一损伤识别。设数据测量仍未包含噪声影响。经10次迭代后识别结果见图3。由图3看出,3个局部损伤位置及损伤程度均能准确识别出来。表明本文所用同伦法能成功识别出结构的多个不同局部损伤,印证本文方法的有效性。
3.1.3 测量噪声影响


图2 耦合梁单一损伤识别Fig.2 Identification of a single damage
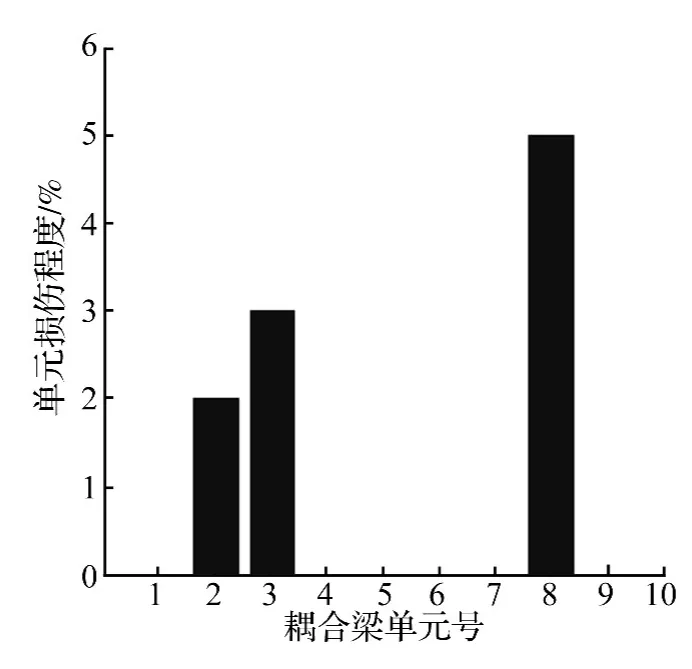
图3 耦合梁多损伤识别Fig.3 Identification of multiple damages
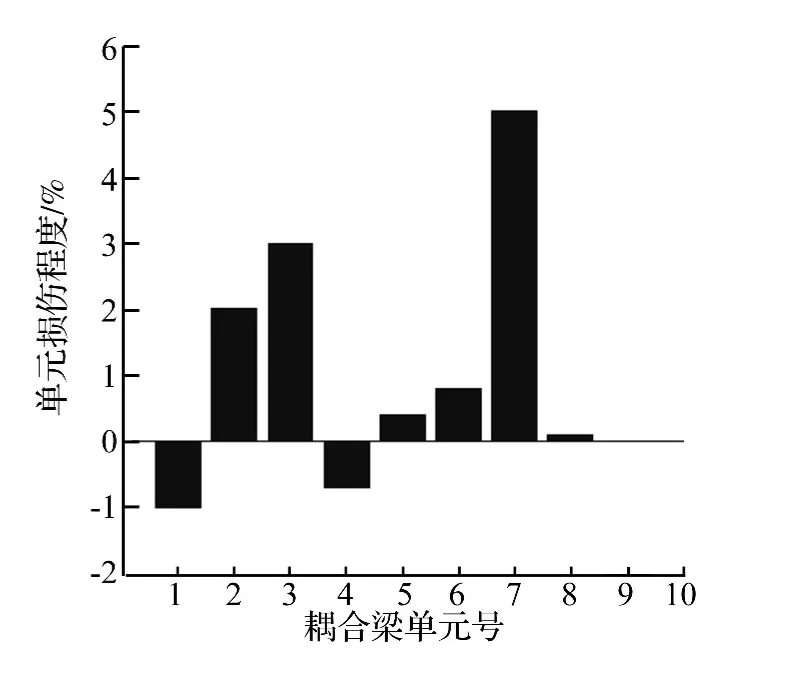
图4 耦合梁的多损伤识别(15% 噪声水平)Fig.4 Identification of multiple damages(15%noise level)
4 结论
本文利用所提基于同伦迭代算法时域损伤识别新方法,对两跨弱耦合欧拉-伯努利梁局部损伤位置及损伤程度进行有效识别。结论如下:
(1)基于同伦迭代算法,识别时解的收敛不依赖于初始值选择。能有效解决重频的多跨结构损伤识别。
(2)此方法对程度较小损伤检测可达到较好精度要求,收敛速度快、损伤识别效率高。
(3)由数值算例知,此方法对测量噪声不敏感,说明具有一定工程实用潜力及应用价值。
[1]Shi Z Y,Law S S,Zhang L M.Damage localization by directly using incomplete mode shapes[J].Journal of Engineering Mechanics-ASCE,2000,126(6):656-660.
[2]Cawley P,Adams R D.The location of defects in structures from measurements of natural frequencies[J].Journal of Strain Analysis,1979,14(2):49-57.
[3]Pandey A K,Biswas M,Samman M M.Damage detection from change in curvature mode shapes[J].Journal of Sound and Vibration,1991,145(2):321-332.
[4]Pandey A K,Biswas M.Damage detection in structures using change in flexibility[J].Journal of Sound and Vibration,1994,169(1):3-17.
[5]Liu J K,Yang Q W.A new structural damage detection method[J].Journal of Sound and Vibration,2006,297(3-5):694-703.
[6]Chen Z J.The analytic of repetition frequency[J].Fu Zhou University Journal(Natural Science),1994,8(4):1-6.
[7]张开鹏,吴代华,李卓球.基于有限元法的结构损伤同伦延拓识别法[J].武汉理工大学学报(自然科学版),2004,14(2):31-34.
ZHANG Kai-peng,WU Dai-hua,LI Zhuo-qiu. Homotopy algorithms of structures damage identification based on FEM[J].Journal of Wuhan University of Technologe(Natural Science),2004,14(2):31-34.
[8]Lu Z R,Law S S.Features of dynamic response sensitivity and its application in damage detection[J].Journal of Sound and Vibration,2007,303(1-2):305-329.
[9]Tikhonov A M.On the solution of ill-posed problems and the method of regularization[J].Soviet Mathematics,1963,4:1035-1038.

