弹道导弹扰动引力快速计算方法的研究
徐晓东 赵建亭 许春雷
(江苏自动化研究所,江苏 连云港 222006)
0 引言
射程在数千千米的远程弹道导弹在沿地球外部上空飞行时,时刻受到地球引力场的作用。由于高速飞行的弹道导弹弹载计算机处理参数的速度和时间非常有限,因此选择计算扰动引力的方法,除要满足一定的计算精度外,还要尽可能的简便,以减少计算量、提高计算速度[1]。由于斯托克斯积分方法和点质量法能够满足导弹制导与导航的精度,在弹道导弹扰动引力计算的工程中广泛应用。但是这两种方法具有计算量大、不能满足快速计算要求的不足;而与梯度法、球谐函数展开法相比较,它们又具有计算精度高和计算范围不受限制的优点,适用于全程弹道导弹弹道扰动引力的计算[2]。实际应用中一般都采用先在地面计算标准弹道附近点的扰动引力,然后通过标准弹道扰动引力插值或逼近来计算实际弹道的扰动引力[3]。
在满足工程需要精度要求的前提下,为了达到弹道导弹扰动引力快速计算的要求,本文在采用斯托克斯积分法计算地球外部空间扰动引力的基础上,提出了简化后的快速计算模型,并根据简化模型的特点,运用并行计算技术来提高计算速度、减少计算时间。仿真试验验证了快速计算模型的有效性。
1 斯托克斯积分原理
采用斯托克斯积分方法计算地球外部空间扰动引力,就是将用斯托克斯积分公式表示的地球外部空间扰动引力位对任一方向求偏导数,以求其扰动引力在该方向上的分量。
假设地球为圆球体时,采用斯托克斯积分公式表示的扰动引力位公式为:
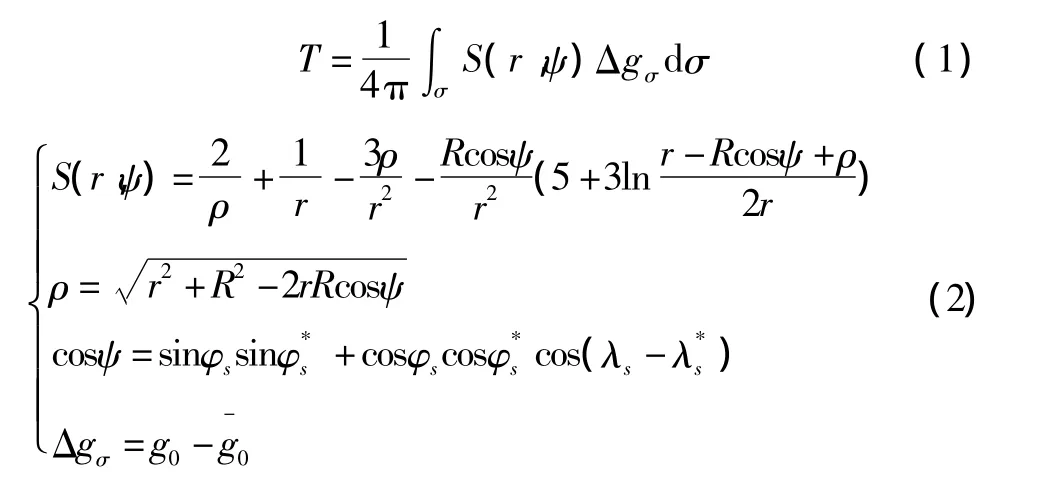
式中:R为地球的平均半径;r为球心到P点的距离;ρ为球面上面积圆dσ到P点的距离;ψ为面积圆dσ与P点间对应的地心极角;φs、λs分别为P点的地心纬度和经度、分别为面积圆dσ的地心纬度和经度;函数S(r,ψ)为广义斯托克斯函数;Δgσ为球面重力异常值[4-5]。
地球扰动引力位示意图如图1所示。

图1 地球扰动引力位示意图Fig.1 Sketch map of the earth gravitational potential of disturbance
2 快速计算模型
2.1 地心弹体坐标系
假设地球是圆球体,坐标原点取在地心,X轴为地心与弹体中心连线的延长线,Y轴在弹道导弹P点的速度V方向与地心构造的平面内,且与X轴垂直,Z轴与X、Y轴构成右手直角坐标系。由此构成的地心弹体坐标系示意图如图2所示。
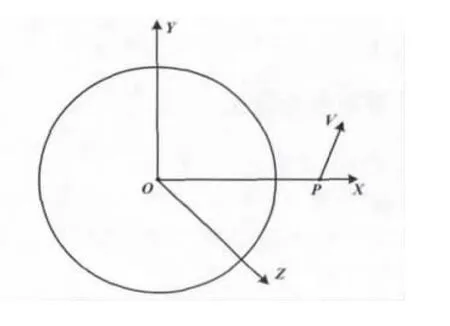
图2 地心弹体坐标系Fig.2 The coordinate system of the geocentric elastomer
2.2 斯托克斯积分简化模型
利用简化的斯托克斯积分法求解外部空间扰动引力模型时,首先将地球以适当的经纬度差(根据实际探测的地面重力异常值区域)进行划分。在划分的基础上,在地心弹体坐标系中,沿着X轴逆向观察,若X轴正方向经过的球体点恰好在某一经纬度差区域内,则以此区域作为起始区域;若X轴正方向经过的球体点恰好在几个经纬度差区域边界上,则以这几个相邻的区域作为起始区域,定义经过的轮次为第一轮,经纬度差区域的个数为N1。接着以X轴为轴心,沿着Y轴和Z轴向外八个方向进行延伸,除了起始区域外,首先经过的经纬度差区域定义为第二经纬度区域,定义轮次为第二轮,经纬度差区域个数为N2。然后继续向外八个方向延伸,除了起始区域和第二经纬度区域外,先经过的经纬度差区域定义为第三经纬度区域,经纬度差区域个数为N3。依次类推,直至当继续外推时出现与上一轮次经纬度差区域相重叠的区域时,将上一轮次经过的经纬度差区域定义为结束区域,经过的轮次定义为M,经纬度差区域个数为NM。
将上述斯托克斯积分法求解外部空间扰动引力积分方程离散化为:
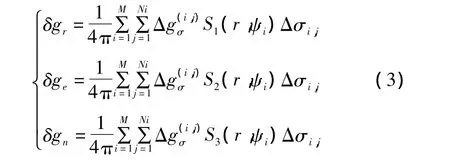
式中:下标r,e,n分别代表天北东坐标系中的三个坐标方向分量。
球面上的经纬度差区域的面积为:
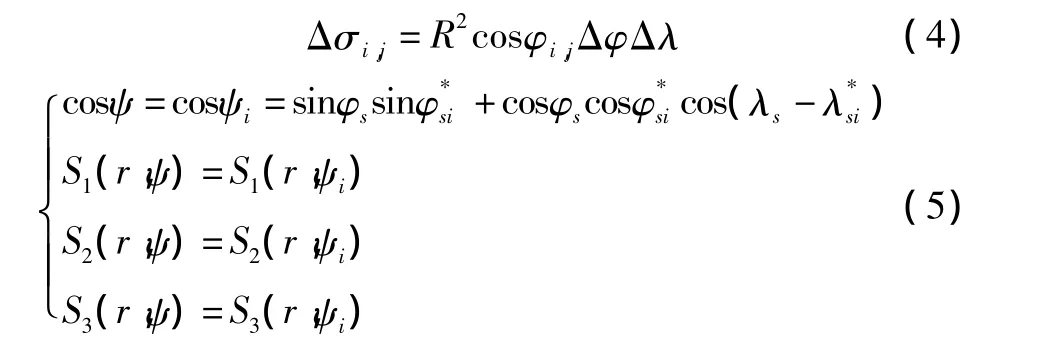
式中:φi为该区域中心的纬度;φ为该区域的纬度、为取自第i经纬度区域中随机选择一个经纬度差区域中心的地心经度和地心纬度(由于假设地球为圆球,则可以认为这些经纬度差区域的r,R,ρ,ψ相等);Δλ、Δφ分别为每一个经纬度差区域四边的经纬度差。
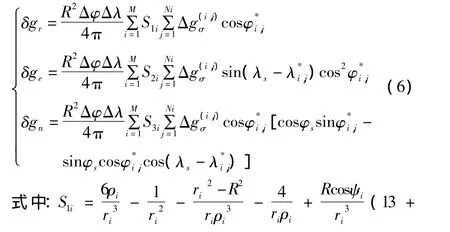

3 并行计算技术
在采用斯托克斯积分法求解弹道导弹外部空间扰动引力的过程中,随着经纬度差的减少,求解的精度会增加,但同时计算工作量以指数倍增加,存在计算工作量大的问题。为了解决这一问题,本文采用并行计算技术来提高计算的速度,以满足实时性的要求。
主从模式是一种比较常用的并行计算架构模式,它有一个控制进程,称为主进程,其余的进程称为从进程。主从架构模式的体系结构如图3所示。
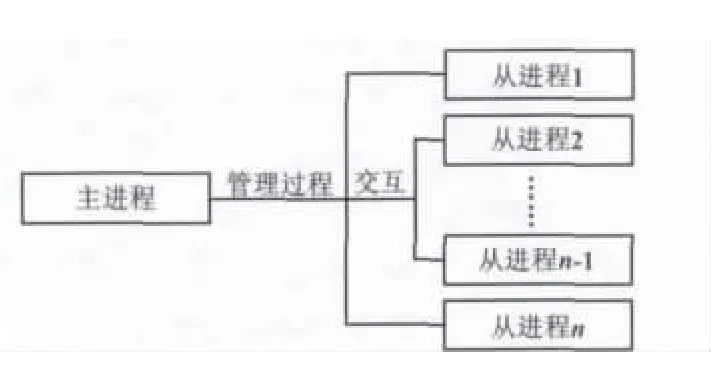
图3 主从模式并行机体系结构Fig.3 Architecture of the master-slave parallel machine
负载均衡问题是影响并行效率的主要因素。在本文的任务分配中,采用地心弹体坐标系左右半球平均分配的原则,使每个处理器中的计算量基本相同,大体能够满足负载均衡的要求。在由三个CPU构成的主从模式并行机构中,程序设计结构框图如图4所示。
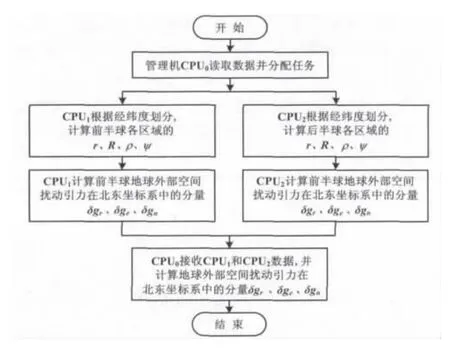
图4 程序设计结构框图Fig.4 Structural block diagram of program design
MPI是一个用于开发基于消息传递并行程序的标准,它提供了一个实际可用、可移植、高效和灵活的消息传递接口库。MPI支持非阻塞通信的方式,即 MPI_Isend(buf,count,datatype,dest,tag,comm,request)能够实现计算和通信的重叠[6],节省了传输数据的时间。同时,MPI还支持基于非阻塞通信模式的广播方式和收集方式。试验证明,与普通的发送(MPI_Send)和接收(MPI_Recv)操作相比,采用广播和收集的方式收发数据更有效。
4 仿真计算
本文采用5°×5°的经纬度差划分方法,将整个球体划分成(360/5)×(360/5)块经纬度差区域,各个经纬度差区域球面上的平均重力异常值Δg(i,j)σ通过数据模拟实现,地球外部空间任一点 P(r,φs,λs)简化的取值为P(7 378 140,0,0),R 取值为地球的平均半径6 371 km,则地球外部空间与球平面的交点为(6 371 000,0,0)。以此交点为中心,沿地心弹体坐标系X轴向周围八个方向进行延伸,这八个经纬度差区域即是第二经纬度区域。以此类推,可以确定其他的经纬度区域。传统计算模型与快速计算方法结果比较如表1所示。

表1 传统/快速计算法的比较Tab.1 Comparison of the fast calculation method and traditional calculation method
表1计算结果表明,简化的快速计算模型与传统的计算方法相比,计算时间降低了33.52%,由此证明了快速计算简化模型的有效性。
为了进一步降低简化的快速计算模型的计算时间,本文引入了如图4所示的并行计算技术。本文在输入相同数据的情况下,比较并行与串行程序的执行时间,并计算相应的加速比和效率。串行/并行计算技术比较结果如表2所示。
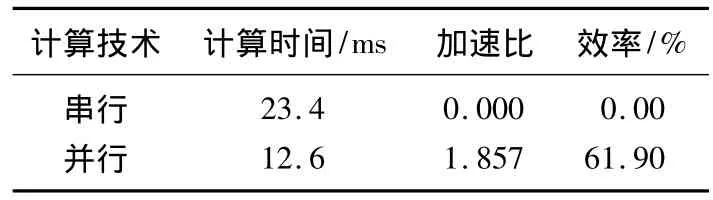
表2 串行/并行计算技术的比较Tab.2 Comparison of serial/parallel computation technology
上述计算结果表明:并行计算方法能够获得较高的加速比和效率,具有比较好的快速计算效果。
5 结束语
远程弹道导弹飞行过程中时刻受到扰动引力的影响,而计算外部空间扰动引力的斯托克斯积分方法本身存在计算量大、模型复杂的不足,不能满足实时计算的要求。针对上述情况,本文提出了斯托克斯解算扰动引力的快速计算模型。通过仿真可知,在满足精度要求的情况下,该模型可以大幅度提高计算速度。同时,针对斯托克斯快速计算模型在计算扰动引力的过程中各个经纬度差区域独立性强的特点,在Linux环境下应用MPI技术实现了斯托克斯积分法的并行计算。仿真验证并行效果明显,能得到较好的加速比和并行效率,从而有效减少扰动引力的计算时间,提高计算的效率。弹道导弹在飞行过程中速度很快,对扰动引力的计算速度提出了很高的要求,研究基于插值和补偿的外部空间扰动引力的快速计算问题,以满足实际应用的需要,将有待于进一步的探讨。
[1]王庆宾,周世昌,王世忠,等.弹道主动段全射向扰动引力快速逼近方法[J].测绘科学技术学报,2010,4(2):79 -81.
[2]张毅,肖龙旭,王顺宏,等.弹道导弹弹道学[M].2版.长沙:国防科技大学出版社,1999:73-76.
[3]王继平,王明海,陈摩西.弹道导弹主动段扰动引力的一种逼近算法[J].航天控制,2008(3):30 -38.
[4] Difrancesco D,Meyer T,Christensen A,et al.Gravity gradiometry:today and tomorrow[C]//SAGA Biennial Technical Meeting and Exhibition,Swaziland,2009:80 -83.
[5]张赤军,骆鸣津,王新胜,等.地球内外扰动物质引起高程异常的分析[J].大地测量与地球动力学,2010,12(6):42 -45.
[6]都志辉.高性能计算并行编程技术-MPI并行程序设计[M].北京:清华大学出版社,2001:99-124.

