基函数自适应选择的预测函数控制方法在混凝投加中的应用

张伯立，章如峰，赵寅军（浙大中控信息技术有限公司，浙江 杭州 310053）

1 引言

预测函数控制[1]在模型预测控制基础上引入了基函数，大大减小了在线计算量，提高了跟踪速度、精度，它利用预测模型及过去、当前时刻输出实现对未来输出的预测，通过优化性能指标来计算控制量，具有良好的跟踪能力及较强的鲁棒性，并在多种领域得到广泛的应用[2,3]。

针对具有大时滞的混凝投药过程控制，预测函数控制具有较好的抗时滞能力。一般固定基函数的预测函数控制在水质不稳定的情况下控制品质不理想，适应性差。由此引出用变基函数的方法对预测函数的控制品质进行改善的设想[4]。当水质变化造成输出结果离期望值较远时，选择一种斜率较大的基函数来快速抑制干扰因素作用；随着输出结果逼近离期望值时，则选择一种斜率较小的基函数来改善控制的超调。由于时滞的原因，我们无法及时判别输出结果离期望值的远近。在此利用BP网络的特性建立一个混凝投药模型，应用该模型预测过程的输出。用该预测输出去与期望值相减得到一个误差，将该误差分为几个区域，每个区域分别对应一个基函数，通过误差来选择对应的基函数。

2 基函数自适应选择的预测控制方法

2.1 基函数自适应器的构造

基函数自适应选择预测函数控制算法与传统预测函数控制相比就是多了一个基函数推理机，这是实现基函数自适应选择的关键。如图1所示。

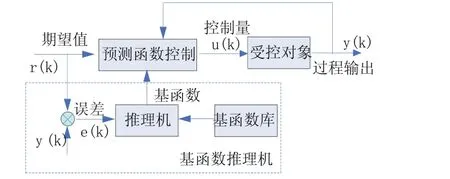
图1 基函数自适应选择预测函数控制算法结构

基函数推理机主要有两大大模块，为基函数库和推理机。

其中基函数库是基础模块，主要是存储所需要的基本基函数。我们可以根据情况有条件的从基函数库中选择所需要的基函数，用该基函数去实现预测函数控制。常用的基函数有阶跃基函数、斜坡基函数和指数基函数等。

而推理机则是核心模块，它里面有一些规则，可以根据一些特定条件从基函数库中选择恰当的基函数。

2.2 不同基函数的预测函数控制对控制品质的影响

下面我分析下基函数对控制量值的影响，从而来评估基函数对控制品质的作用。

一般过程的方程表示如下：

预测函数控制算法控制量表述如下：

式中f()i第i个采样周期的基函数取值，µ是基函数的线性加权系数。把（2）代入（1）得：

选择优化指标函数取为误差平方和，

式中ry为期望轨迹，py为过程预测轨迹，my预测模型值，e为过程补偿误差。令

则优化指标函数形式改为，

极小化优化指标函数，则组合系数计算公式如下，

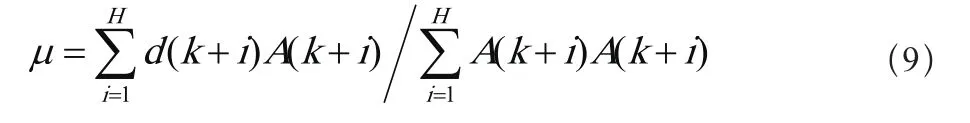
那么预测时域内第一步预测控制量结果如下，

我们选择阶跃基函数、斜坡基函数和指数基函数来比较它们对控制品质的影响。如表1所示，A1(k+i)、1µ和1u表示为阶跃基函数时A(k+i)、µ和u值；A2(k+i) 、2µ和2u表示为斜坡基函数时A(k+i)、µ和u值；A3(k+i)、3µ和3u表示为指数基函数时A(k+i)、µ和u值。从表1中可以看出，A1<>2µ，而2µ>>3µ；最后得出，1µ>>2µ，而2u>>3u。

表1 不同基函数的u比对

根据上述比较得出，阶跃基函数的控制量调节幅度是最高的，这就会造成较大的超调；指数基函数的控制量调节幅度是最低的，这就使响应速度很慢；斜坡基函数的控制量调节幅度居中。

2.3 基函数自适应选择的算法

基函数自适应选择算法的规则如下：当水质变化造成输出结果离期望值较远时，选择一种斜率较大的基函数来快速抑制扰动作用；随着输出结果逼近离期望值时，则选择一种斜率较小的基函数来改善控制的超调。

图2 基函自适应选择数算法

基函数自适应选择算法流程图如图2所示，具体算法如下：

（1）建立模式匹配库。

（2）读入k时刻y(k)，期望设定值

（3）计算误差，判断误差类别。

（4）确定类别，确定模式，选择基函数。

（5）无法确定类别，保持不变，选择原来的基函数。

模式匹配库建立方法如下：

第一步确立基函数模式库：常用基函数斜率从小到大排为阶跃函数、斜坡函数和指数函数，将这三个基函数分别定为模式A、模式B和模式C；

第二步确立输出误差类别：将过程输出值与期望值的误差集合分为三个类别，分别是类别a、类别b和类别c；

第三步建立基函数模式与输出误差类别的匹配关系：类别a对应模式A，类别b对应模式B，类别c对应模式C。

本文的误差分类方法：

一是把误差集合归一化到区间（0，1）中；

二是取两个节点d1和d2，将（0，1）区间分为（0，d1）、（d1，d2）和（d2，1）三个区间。

这里类别a就是区间（0，d1），同理类别b就是区间（d1，d2），类别c就是区间（d2，1）。

推理机的判别方法，令当前时刻过程输出值与期望值的误差为E，其量程为(0 ，Emax)，将其归一化至（0,1）范围。

判别出e所属区间。若e在（0，d1）区间，则选择基函数中的模式A；若e在（d1，d2）区间，则选择基函数中的模式B；若e在（d2，1）区间，则选择基函数中的模式C；这里的d1和d2可以根据不同情况确定。

3 混凝投加过程基函数自适应选择的预测控制的设计

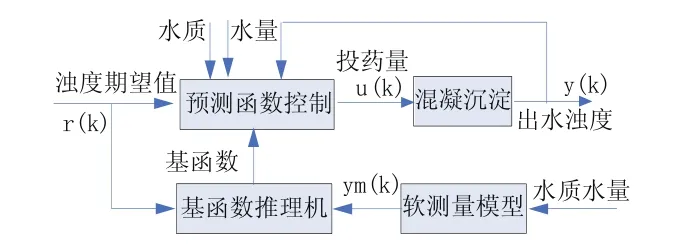
图3 基函数自适应选择混凝投药PFC算法

基函数自适应选择混凝投药PFC算法如图3所示，混凝投药PFC控制器包括传统预测函数控制、基函数推理机和混凝沉淀过程软测量模型。软测量模型是算法中的一个关键环节，因为在推理机判别过程中我们需要知道当前时刻过程输出值与期望值的误差，但是由于时滞的原因，我们无法及时的知道当前时刻水质水量所造成的输出结果。在此就需要利用软测量方法建立一个混凝投药模型，应用该模型来预测当前时刻过程的输出。

混凝投加过程基函数自适应选择的预测控制的设计主要有基函数推理机设计和软测量模型设计，设计如下：

根据文献[5]和文献[6]，本文预测函数控制器设计如下。

参考轨迹设计如下，

式中c(k+)i为出水浊度指标，一般为0.1。

过程预测轨迹设计如下，

优化指标函数设计如下，

式中H为预测时域，一般为100。预测模型设计如下，

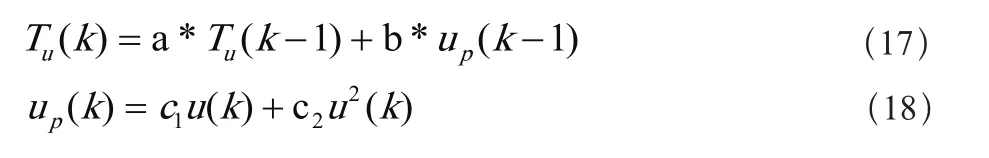
式中u为加矾流量，uT为沉后浊度。

（2）基函数推理机设计

现代水厂出水浊度标准≤0.1 NTU，假设进水水质水量出现突变，此时出水浊度预测为x NTU。采用推理机误差分类方法，设定d1为0.1×（x-0.1），d2为0.4×（x-0.1）。由此确定，预测出水浊度在（0.4×（x-0.1），x-0.1）区间时，选择阶跃基函数；预测出水浊度在（0.1×（x-0.1）,0.4×（x-0.1））区间时，选择斜坡基函数；预测出水浊度在（0,0.1×（x-0.1））区间时，选择指数基函数。则设计得到类别a为（0.4,1），类别b为（0.1,0.4），类别c为（0,0.1）。同时设计规定模式A为阶跃基函数，模式B为斜坡基函数，模式C为指数基函数。最后设计规定类别a匹配模式A，类别b匹配模式B，类别c匹配模式C。

（3）软测量模型设计

混凝投加过程基函数自适应选择的预测控制的设计主要软测量方法有很多，常用的有回归建模方法、BP神经网络建模方法和模糊建模方法等。本文利用BP网络强大的非线性逼近能力来建立混凝投药过程模型。BP神经网络的建立需要确定两个因素，一是BP神经网络的输入输出，二是BP神经网络的网络层数。已证明三层BP网络可以逼近任意非线性特性，因此本文所建立的混凝投药模型神经网络层数为3。通常混凝沉淀过程中影响输出浊度的因素主要为进水水量、进水浊度、温度、PH值和投药量。根据文献[7]和文献[8]，本文的BP神经网络模型的输入变量选择为进水水量、进水浊度、温度、PH值和投药量，输出为出水浊度。混凝投药过程BP神经网络模型结构如图4所示。

图4 混凝投药过程BP神经网络模型结构

4 算例

采用某水厂的混凝投药过程作为控制算法的仿真对象，其中控制量为加矾流量，被控量为沉后水浊度，参考第三节预测函数控制器设计中的预测模型设计方法，应用某水厂的历史数据为仿真实验数据，把该数据分为两部分，分别用来辨识控制器的预测模型和仿真过程的对象模型。对象模型如下，

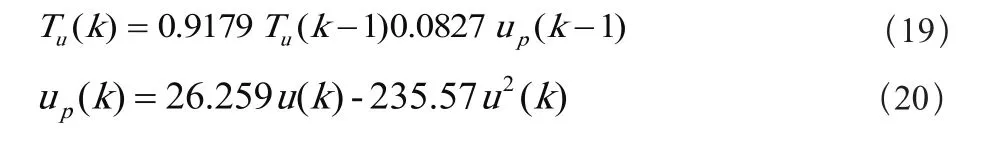
式中u为加矾流量，Tu为沉后浊度，把上述的模型作为仿真实验的实际过程对象。控制仿真试验在matlab环境下用m语言实现，算法流程图如图5所示，具体算法如下：

（1）确定采样周期、预测时域程度、参考轨迹系数及期望过程输出值。

（2）读入k时刻y(k)，期望设定值

（3）获取水质水量值，估计输出浊度值，计算误差，找到匹配基函数，计算u1(k+1)。

（4）令k=k+1，并判断k是否小于仿真步数N。

（5）是转（2），否结束。

图5 仿真算法流程图

仿真研究基函数自适应选择投药预测函数控制参数设置，在800秒时浊度设定值c()k为0.2NTU，采样周期sT为2秒，参考轨迹响应时间rT为2秒。仿真结果如图6所示，纵坐标为出水浊度值，单位为NTU，横坐标为仿真时间，单位为秒。图6中的a为基函数自适应选择情况下做的PFC仿真，图6中的b为阶跃基函数PFC仿真。看图6（a）和图6（b），阶跃基函数PFC控制在十几秒内迅速接近期望值，响应速度快，然后输出超越期望值，变为0.29 NTU，直到150秒后才平稳，超调大；而基函数自适应选择PFC控制在十几秒内迅速接近期望值，变为0.18 NTU，响应速度快，然后输出缓慢接近期望值，到100秒后缓慢平稳，无超调。可以看出，对于具有大时滞时变特性的投药过程，基函数自适应选择投药PFC控制能较快较稳定地达到设定值，响应速度快、超调小。

5 结语

基于模式匹配或外部干扰较大的基本思想，通过事先设定的推理规则，根据期望值与实际预测值的差从基函数库中选出匹配的基函数，实现基函数自适应选择预测函数投药控制。通过基函数自适应选择，可以同时兼顾系统超调和响应速度，保证混凝投药控制系统的稳定。

图6 基函数自适应选择预测函数控制与阶跃基函数预测函数控制仿真效果

[1]王国玉, 韩璞, 王东风. 预测函数控制及其应用研究[J]. 系统仿真学报,2002.14 (8) : 1087～1091.

[2]H.Bouhenchir, M.Cabassud, M.V.Le Lann. Predictive functional control for the temperature control of a chemical batch reactor[J]. Computers & Chemical Engineering, 2006.30: 1141～1154.

[3]Ridong Zhang, Shuqing Wang. Support vector machine based predictive functional control design for output temperature of coking furnace[J]. Journal of Process Control, 2008. 18: 439～448.

[4]赵寅军, 陈国定, 张伯立. 阶跃基权系数时变的预测函数控制[J]. 计算机仿真, 2012.1 (29) : 79～82.

[5]葛宝明, 林飞, 李国国. 先进控制理论及其应用[M]. 机械工业出版社,2007.

[6]丁宝苍. 预测控制的理论与方法[M]. 机械工业出版社, 2008.

[7]白桦, 李圭白. 基于神经网络的混凝投药系统预测模型[J]. 中国给水排水,2002, 18 (6) : 46～47.

[8]李丽荣, 韩璞, 董泽等. 人工神经网络在系统辨识中的研究与应用[J]. 华北电力大学学报, 2000, 27 (3) : 28～33.