广告主异质下的关键词拍卖的最优保留价研究
王 平,张玉林
(东南大学经济管理学院,江苏南京 211189)
1 研究背景
关键词拍卖是近十几年来搜索引擎发展起来的一种广告服务形式。该模式起源于1998年的GoTo(即后来雅虎的Overture),Google在2002年改进了其中的拍卖机制,成功地将广义二阶价格拍卖[1](generalized second price auction,GSP) 转变为商业模式,该模式很快成为互联网广告的主要利润来源[2]。在Google公司30亿美元的月广告收入中,最大的贡献来自搜索关键词广告[3]。中国2011年搜索引擎广告整体市场规模达154.9亿元人民币,占网络广告总体市场规模的比例超过50%,搜索引擎已超过报纸媒介成为仅次于电视的第二大广告载体[4]。百度也在其广告服务中采用了关键词拍卖,短短几年就成为国内最大的互联网企业。关键词广告的成功应用引起了学术界的广泛关注,也为相关的理论研究赋予了很高的实际价值。
在关键词销售实践中,大多数关键词广告是这样设计的:广告主根据所需要推广的产品选择一组关键词(由搜索引擎发布),并为每个关键词提供一个报价。该报价表示当用户点击其广告时,广告主愿意支付的最高价格。当用户检索某个关键词时,搜索引擎会反馈给用户一个搜索结果页面(SERP),SERP上除了搜索引擎的算法自动检索生成的内容外,还会在特定的位置出现一组有序的广告,这些广告就是广告主选择该关键词并提交了报价的广告,它们的排序也依赖于广告主的报价。这一过程中,广告主的报价反映了其对单位点击的私有估价信息,拍卖机制决定了广告位的预期分配以及广告主的预期支付,最后用户的点击实现了广告资源的分配,从而使搜索引擎获得收益。
实践中,关键词拍卖机制大致经历了两个阶段,即广义第一价格(GFP)和广义第二价格(GSP)。GFP机制简单易行,但不稳定,很快被GSP机制代替。目前,GSP机制已成为主流搜索引擎服务商关键词拍卖的主要机制,众多学者围绕该机制展开了研究。GSP机制是EDELMAN等在总结Google和Yahoo!关键词拍卖的基础上提出的,他们证明该机制存在局部无嫉妒均衡(locally envy-free equilibrium),在这种均衡下广告主没有动机改变自己的位置,文献[5]提出的对称纳什均衡(symmetric Nash equilibrium)与此相同。文献[6]则给出了不同排序方式下GSP机制的均衡。文献[7]分析了在GSP机制下广告主的策略性行为,证明了这种策略行为不利于搜索引擎的收益。文献[8]则在GSP机制的基础上提出按广告主竞价或者加权竞价递减排序的“阶梯拍卖”,并证明了这是一个讲真话机制。而文献[9]认为GSP机制并不是对所有的广告商都公平。但是这些结论都是在没有考虑广告主预算约束和关键词保留价的前提下得到的。当广告主有预算约束时,上述结论将发生改变,如文献[10]讨论了广告主有预算约束的拍卖机制,他们认为有预算约束时不存在非平凡的讲真话机制;而当存在保留价时,上述结论将发生变化,如文献[6]给出了广告主的单阶段和多阶段竞价均衡,并证明了保留价会影响广告主的均衡竞价。因此,广告位有保留价约束时,已有的多数关键词拍卖的研究成果需要修订和补充。
保留价的思想起源于RILEY等1981年的研究单物品拍卖工作[11-12],其在私有估价假设与竞价者风险中性假设下,得到了最优保留价的经典公式。文献[13]则对二阶和一阶价格拍卖中的最优保留价进行了分析,发现最优保留价受参加拍卖人数影响,并且设置保留价的效果比吸引更多的竞拍者的效果要好。关键词拍卖出现后,上述经典结果被推广应用于关键词拍卖,如文献[14]为每一个广告位设置保留价,提出“双阶梯拍卖”,推广了文献[8]的结论。文献[15]认为广告位可变成本的作用相当于保留价的作用,并可利用广告位可变成本实现最优关键词拍卖。文献[16]提出了在广义英式拍卖中关键词最优保留价应满足的关系式。在处理方法上,有学者将关键词拍卖看作可分物品拍卖,比较重要的有文献[17],文献[18]则沿用这一方法,在广告主独立且同质对称下,以搜索引擎收益最大化为目标,推导出关键词的最优保留价。但是,实际中广告主之间相互独立却不对称的情况是普遍存在的。对搜索引擎来说,不同的广告商有不同的竞价策略,从而产生不同的支付,进而影响预期收益[19]。因此,在广告商异质性的一般假设下研究关键词的最优保留价,显然具有重大的理论和实际意义,该问题也是笔者研究的重点,是与已有研究的区别之所在。
2 机制描述
现实中的关键词拍卖十分复杂,各大搜索引擎的拍卖规则也不尽相同,如Yahoo!的直接排名机制和Google的综合排名机制。但物品的出售机制总是包括以下要素:买者的可能信息或者报价的集合,这里表现为对关键词的估价;一套分配规则;以及一套支付规则。
首先假设有关键词A,搜索引擎在其下设置了 k 个广告位,用 j表示,j∈K(K=1,2,…,k),有n 个潜在广告主,令 i∈N(N=1,2,…,n)为广告主i的标记,对广告主和搜索引擎作如下假设:
(1)假设广告主人数多于广告位数,即n≥k,且拍卖的所有参与者都是个体理性的;
(2)广告主的估价υi为私有信息,但假设其服从的分布是公共知识;
(3)广告主独立非对称。如果广告主i的估价υi服从概率分布 Fi(·),概率密度函数为fi(·),那么当 i≠j时,Fi(·)≠Fj(·);
任意广告主在搜索结果页面上的位置由自己的报价和其他广告主的报价共同确定,记广告主i的报价为bi,其预期点击率Pi和预期付费Mi为:
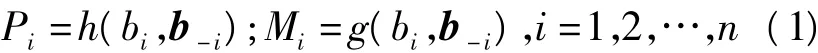
其中:h为分配规则;g为支付规则;b-i=(b1,b2,…,bi-1,bi+1,…,bn)。
广告主根据自己对关键词的估价进行报价,有:

βi(·)称为广告主i的策略。在非合作博弈中,重要的是要找到它的均衡策略,因为均衡策略是所有广告主的最优选择。所谓均衡策略见定义1。
定义1 均衡策略β(·)满足:
(1)所有的广告主都按照策略β(·)出价,即对任意广告主i,都有βi=β;
(2)如果其他广告主都按照b-i=β(υ-i)出价,即其他广告主都选择在出价策略中显示自己的真实估价,那么对于真实估价为υi的广告主来说,其最优反应也是显示自己的真实估价,即bi=β(υi),定义 β(υi)=υi。
这样,独立但不同分布的私有估价υi,均衡策略β(υi)以及式(1)共同构成了关键词广告的出售机制。下面将在这一机制中考虑保留价,研究关键词最优保留价设置。
3 搜索引擎的收益
考虑广告主i,记λij为其在位置j时所获得的点击率,如果其想通过隐瞒自己的真实估价来获得更多收益,那么其将报价bi而非真实估价υi。此时,他的预期点击率和付费分别为:
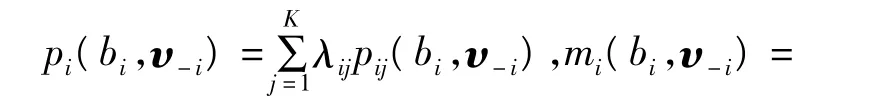
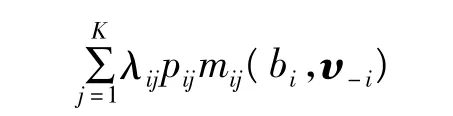
式中:pij(bi,υ-i)和 mij(bi,υ-i)分别为广告主i报价bi,而其他广告主按真实估价报价时得到位置j的概率和付费。
假设除广告主i外其他广告主都按真实估价报价,即b-i=υ-i时,广告主i的预期利润为:

进而,广告主i的期望利润为:
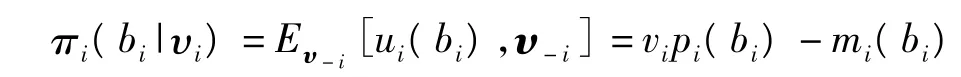
其中:Eυ-i(·)表示对i外的其他n-1个广告主的估价分布取期望,pi(bi)=Eυ-i·[pi(bi,υ-i)],mi(bi)=Eυ-i[mi(bi,υ-i)]分别表示广告主i报价bi时的期望点击率和期望支付。
个体理性的广告主i会保证收益非负,找到保证期望利润至少为0的估价下限,那么:
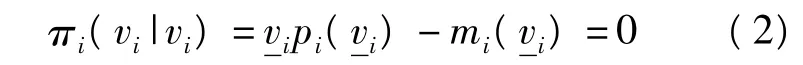
同时,希望找到一个合适的bi使自己的期望收益最大,目标函数为:

为了获得最大的收益,广告主i需要确定最优的bi。由定义1知bi=vi是一个均衡策略,即当其他广告主均按真实估价报价时,广告主i的最优反应是显示真实估价,因此bi=vi是最优化式(3)的解,从而如下的一阶条件成立:

当vi大于时,上述微分方程成立。结合个体理性条件式(2)可得广告主i的期望支付为:

从搜索引擎的角度来看,由式(4)得到的期望支付mi(vi)仍然是一个随机变量,因为搜索引擎仅知道vi的分布,所以搜索引擎从广告主i处得到的期望收益为:

通过简单的积分变换可得:

搜索引擎的总收益是从各广告主处得到的收益之和,即:

4 最低保留价
由(6)式可知,搜索引擎的最优化问题为:

根据基本假设可知hi(vi)单调递增,结合式(8)和式(9)可知,对于任意,有:

结论1 假设关键词拍卖的所有参与者都是风险中性的,竞价者的估价是独立非对称的,则搜索引擎应设定的最优保留价为:

如果广告主独立对称,即当F1=F2=…=Fn=F,f1=f2=…=fn=f时,可以得到=…==v*,从而结论1可以写为:r*=v*,其中v*满足式(10)。这与文献[18]中独立同分布的广告主私人价值假设下,搜索引擎对关键词的持有价值为零时的最优保留价一致。根据文献[1],广告位对于搜索引擎来说是一种易逝品,持有广告位而不出售是不会有收益的,其持有价值为0。在这一假设前提下,文献[18]中的结论就是笔者结论的一个特例。
综合上述广告主的估价是独立同分布时的保留价及其满足的性质,可得到结论2。
结论2 如果关键词拍卖的所有参与者均为风险中性,竞价者的估价是独立同分布的,那么随着最优保留价的提高,广告主得到广告位的概率降低。
证明 由上述分析可知,当广告主的估价独立同分布时,根据式(10)可得:
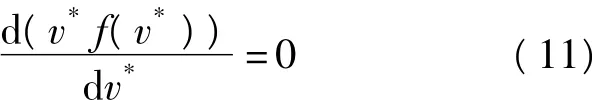
对上式两边同时求不定积分可以得到:

其中,C为不定积分产生的任意常数。
已知F(v*)为累计概率,因此F(v*)≤1,从而C≤1,则式(12)右边是大于等于0的。式(12)表示广告主估价大于最优保留价的概率随着最优保留价的增加而降低,广告主得到广告位的概率与最优保留价之间也满足该关系,这是符合实际情况的。随着保留价的提高,广告主真实估价大于保留价的概率就会减小。因此,搜索引擎应选择适当的保留价,保证参与拍卖的广告主人数以及自己的收益。
分析上述广告主独立对称和非对称情况下保留价所满足的性质,可得到结论3。
结论3 如果关键词拍卖的所有参与者均为风险中性,在广告主的估价是独立对称的私人价值假设下,搜索引擎对关键词的最优保留价与广告主人数以及参与拍卖的广告主没有关系;当广告主的估价独立非对称时,搜索引擎的最低保留价格受到参与拍卖的竞价者的影响,但两者仍没有直接联系。
5 算例分析
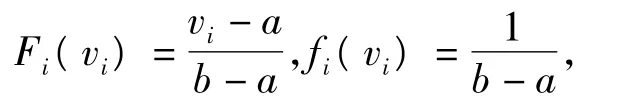
假设搜索引擎在某关键词下设置5个位置,且广告主的期望点击率为:P=(0.10F1(v1),0.08F2(v2),0.06F3(v3),0.04F4(v4),0.07F5(v5),0.09F6(v6),0.03F7(v7),0.05F8(v8),0.02F9(v9),0.20F10(v10)),并保持固定不变。
表1给出了竞价人数从5到10时关键词保留价和搜索引擎总预期收益变化结果。
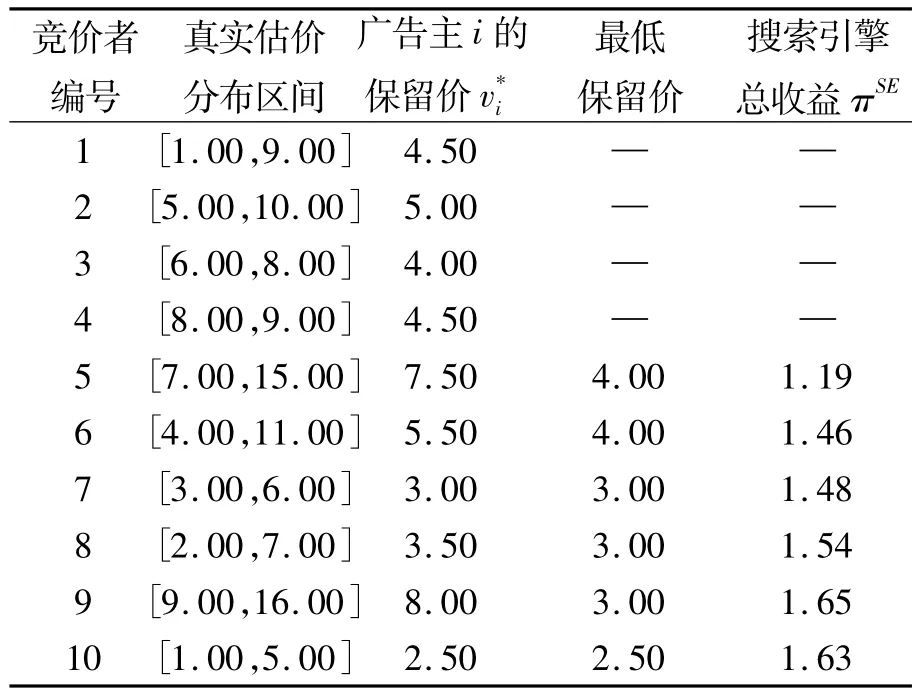
表1 不同竞价者情形下的最低保留价与搜索引擎总收益
从表1可以看出,在考虑广告主异质性时,当广告主人数从5增加到8时,关键词最低保留价不变,当广告主9加入时,关键词保留价减小,而广告主10加入时,关键词保留价不变,由此初步推断,关键词最低保留价与广告主人数无关,但与新加入的广告主的估价所服从的具体分布相关。同时,随着广告主人数的增加,搜索引擎的总预期收益也增加,这是符合实际的。直观地说,广告主人数越多,搜索引擎分配广告位时的选择范围越大,从而有可能获得更多收益。
6 结论
笔者将关键词拍卖看成可分单物品拍卖,在考虑广告主异质性的情况下,设计了一个搜索引擎关键词拍卖机制,得到了关键词最优保留价所满足的理论表达式。与文献[18]相比,笔者的结论更为一般化。该研究对点击率的假设也更加符合实际,点击率既与位置有关,又与广告主有关,且无论其是否符合可分离假设对笔者的结论都没有影响。还讨论了在广告主的估价独立且同分布时保留价对广告主的影响,发现保留价提高时广告主得到广告位的概率就降低。这意味着,搜索引擎应选择适当的保留价来保证广告主的参与以及自己的收益。实际情形下,保留价的影响因素有很多,更多影响因素下的关键词最优保留价研究是值得进一步讨论的问题。
[1]EDELMAN B,OSTROVSKY M,SCHWARZ M.Internet advertising and the generalized second price auction:selling billions of dollars worth of keywords[R].[S.l.]:[s.n.],2005.
[2]FAIN D C,PEDERSEN J O.Sponsored search:a brief history[C]//Proceedings of the 2006 ACM Conference on Electronic Commerce.Ann Arbor:[s.n.],2006:12-13.
[3]DCCI互联网数据中心.搜索竞价排名,美仍继续[R].[S.l.]:DCCI互联网数据中心,2011.
[4]DCCI互联网数据中心.2010—2011年度中国互联网市场数据发布[R].[S.l.]:DCCI互联网数据中心,2011.
[5]HAL R V.Position auctions[J].International Journal of Industrial Organization,2007(25):1163-1178.
[6]陈李刚,李一军.搜索引擎关键字广告的竞争分析[J].中国管理科学,2010,18(5):98-105.
[7]BENJAMIN E,MICHAEL O.Strategic bidder behavior in sponsored search auctions[J].Decision Support Systems,2007,43(1):192-198.
[8]GAGAN A,ASHISH G,RAJEEV M.Truthful auctions for pricing search keywords[C]//Proceedings of the 7th ACM Conference on Electronic Commerce(EC-06).[S.l.]:[s.n.],2006:1-7.
[9]MAUTIZIO N,GIUSEPPE D A,GIUSEPPE F I.The value of location in keyword auctions[J].Electronic Commerce Research and Applications,2010(9):160-170.
[10]EYAL E D,JON F,YISHAY M,et al.Position auctions with bidder-specific minimum prices[C]//Ad Auctions Workshop(2008).[S.l.]:[s.n.],2008:577-584.
[11]RILEY J G,SAMUELSON W F.Optimal auctions[J].The American Economic Review,1981,71(3):381-392.
[12]MYERSON R B.Optimal auction design[J].Mathematics of Operations Research,1981,6(1):58-73.
[13]STEPHANIE R,PATRICK W S.Reserve prices in auctions as reference points[J].The Economic Journal,2007(117):637-653.
[14]RICA G,SERGEI V.Sponsored search auctions with reserve prices:going beyond separability[C]//Internet and Network Economics,LNCS.[S.l.]: [s.n.],2008:597-608.
[15]LIU S L,RONG W J.Optimal keyword auctions with variable costs of advertisement[R].[S.l.]:[s.n.],2011.
[16]BENJAMIN E,MICHAEL S.Optimal auction design and equilibrium selection in sponsored search auctions[EB/OL].[2013-01-12].http://ssrn.com/abstract=1535319.2011.
[17]CHEN J Q,LIU D,ANDREW B W.Designing share structure in auctions of divisible goods[C]//The ACM Conference on Electronic Commence(EC’05).Vancouver:British Columbia,2005:786-791.
[18]戎文晋,刘树林.关键词拍卖中最优保留价的研究[J].管理科学学报,2010,13(4):29-37.
[19]姜辉,王浣尘,关树永.付费搜索拍卖建模与两类排名机制比较研究[J].中国管理科学,2009,17(3):142-149.

