重排谱图在跳频信号参数估计中的应用

邓 灵，张天骐，金 静，朱洪波

（重庆邮电大学 信号与信息处理重庆市重点实验室，重庆400065）

0 引 言

跳频通信以其优良的抗干扰性能和多址组网性能在军事、民用通信得到了广泛的应用，于是如何对接收到的跳频信号进行检测和分析，获得频率，周期等技术参数以便通信双方使用，已经成为一种迫切需要［1，2］。

跳频信号不同于一般的平稳信号，其频率不断地跳变。对于这类非平稳信号，常用时频分析来处理。经过长期大量的研究，这些主要的时频分析方法显露了很多缺陷。短时傅里叶变换 （short－time fourier transform，STFT）虽然运算量小，但是时间和频率的分辨率不高［3］；维格分布（wigner－ville distribution，WVD）具有许多优良的数学性质，但对于跳频信号存在很大的交叉项干扰［4，5］；平滑伪维格分布 （smoothed pseudo WVD，SPWVD）通过分别在时域和频域进行平滑，有效地抑制了交叉项干扰，但降低了时频分辨率［6，7］；重排类时频分布在时频聚集性和抑制交叉项干扰上都有良好的性能，考虑到参数估计需要精确的估计值，本文采用了重排谱图的时频分析方法，对跳频信号进行参数估计。

重排谱图的方法能有效地减少交叉项干扰，提高了时频分布的聚集性，同时保留了维格分布的高时频分辨率，使跳频参数的估计值更加准确。首先利用重排谱图，对跳频信号进行处理，提取出重排谱图在每个时刻的最大值，构成峰值矢量，对峰值矢量进行傅里叶变换，由频谱峰值位置即可得出跳频周期，在已知跳频周期的基础上，利用公式求出跳变时刻及跳频频率。

1 跳频信号的时域特性

跳频信号的主要参数有跳频频率、跳频周期、跳变时刻及跳频图案，其定义参见文献 ［8］。常用的数学表达式如下

式中：0≤t≤T，T为跳频信号的观测时间；A为幅度；p为跳频信号的载波频率个数；recTh是宽度为Th的矩形窗；Th为跳频信号的跳频周期；｛ f1，f2，…，fk，…，fp｝ 为一个给定的频率集，fk为跳频信号的第k个跳变频率；φ为载波的初始相位；n（t）为零均值的加性高斯白噪声。

理想的跳频信号 （无噪声）如图1所示，其中，初始相位为φ＝0，跳频周期为Th＝0.05s，观测时间T为5个跳频周期，采样频率fs＝1000Hz，采用的跳频频率为｛350，400，150，50，250｝Hz。

图1 时域中的观测信号

2 时频分析方法

2.1 短时傅里叶变换 （STFT）及谱图

短时傅里叶变换是一种典型的线性时频表示［8］。给定一个窗长很短的窗函数γ（t），让窗在时间域上滑动，则信号z（t）的短时傅里叶变换定义为

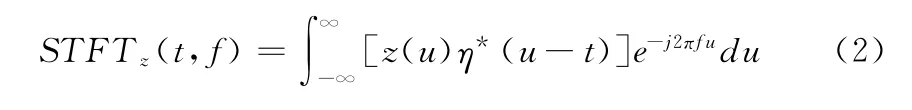
定义式表明，信号在时间t的短时傅里叶变换就是首先让信号乘以一个以时间t为中心的窗函数η＊（u－t），然后对乘积作傅里叶变换，相当于提取了信号在时间t附近的一个切片进行分析，因此其物理意义可看成是信号z（t）在时刻t附近的一个 “局部频谱”。窗函数的选择对局部频谱的分辨率有明显影响，窗宽要适应信号的局部平稳长度，如何找到最优的窗函数使短时傅里叶变换在实际应用中受限。

由于能量本身就是一种二次型表示，当我们用时频分布来描述时间－频率能量分布时，二次型时频表示更加直观，谱图便是二次型时频表示的一个典型例子。谱图的定义为STFT的模值的平方

对于一般时变性比较明显的信号，用谱图来分析只能取很短的时间窗宽，因此存在时宽和带宽分辨率的矛盾；但是对于多分量信号z（t）＝∑izi（t），谱图的计算式为

式中：φzi（t，f）＝arg（STFTzi（t，f）），由上式可知，如果信号自身的谱图不重叠，那么谱图没有交叉项。

2.2 维格分布 （WVD）

信号z（t）的维格分布定义为

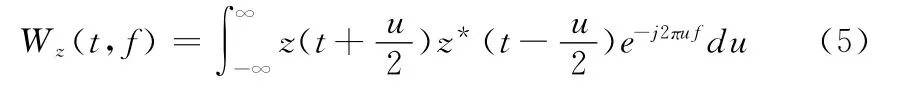
对于多分量信号，不同信号分量之间交叉作用是比较严重，即使两个信号分量的支撑区基本不重叠，维格分布仍会出现交叉项。由于维格分布严重的交叉项干扰，限制了它的实际应用。

2.3 重排谱图

对于以上二次型时频分布的不足，Kodera K，De Villedary C等人首先提出了对谱图进行重排，来提高信号分量的时频聚集性。随后，Auger.F，Flandrin.P提出了比较完善的重排公式［9］。

根据前面的定义，谱图可以看成是信号和分析窗之间的维格分布的二维卷积，即

式中，Wh是窗函数的维格分布。式 （7）表明，乘积项Wz（s，ξ）W （t－s，f－ξ）之和即任意点 （t，f）在时频平面的值，可看作是对（t，f）的邻近点的维格分布值进行加权平均。因此，信号的谱图是信号在以点（t，f）为中心的邻近区域内的能量平均值。这一求平均的运算虽减小了信号的交叉项，同时也使信号的分量发生了扩散［10，11］，重排方法通过重排算子，重新安排信号的能量在时频域内的分布，将各平均点分配到能量重心，以改善信号分量的能量聚集性。其中，重排算子定义为

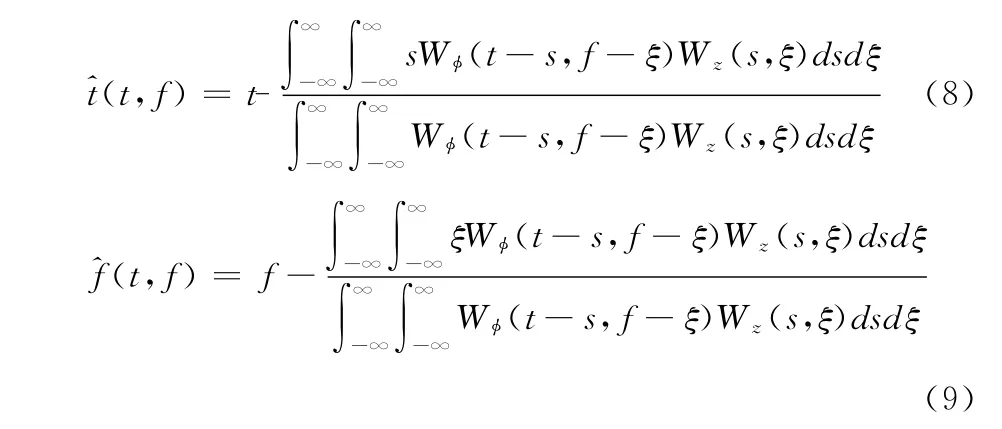
2.4 谱图、WVD及重排谱图方法的比较

在理想的跳频信号中加入信噪比为10dB的高斯白噪声，分别用WVD、谱图和重排谱图进行仿真，得到如图2－图4结果所示。

由图2－图4可以看出，WVD在有噪声的情况下，跳频图案模糊，各分量间 （不同频点之间，频点与噪声以及不同频率的噪声之间）存在严重的交叉项干扰；谱图通过加权求平均，交叉项干扰显著减少，跳频图案比较清晰，但是由于窗函数的选取受限 （此处选用了窗长为61的汉宁窗），导致其时频分辨率很低；重排谱图方法在谱图的基础上，通过重新分配信号的能量分布提高了时频聚集性，能够清晰准确地反映出跳频信号的时频特性，便于参数估计。

图4 重排谱图

3 跳频信号的参数估计

对于接收到的跳频信号以跳频信号模型的采样频率fs进行采样，得到长度为N的序列z（n），n＝0，1，…，N－1，具体的参数估计算法步骤如下：

跳频周期

（3）用FFT变换对最大值矢量y（n）进行处理，跳频信号的跳频速率fmax可由变换后的幅频图直接读出，即幅度最大值所在的频率点。继而得到跳周期估计值＝其相应的离散估计值为。

跳变时刻

（1）在实际应用中，第一个周期和最后一个周期可能会因为接收不完整而存在较大的误差，作精确估计时只对中间的几个周期进行计算。求出y（n）在观测时间n∈［＾NH＋1，N－＾NH］内峰值所在的位置，得到p（k），k＝1，2，…，p，p是观测出的峰值个数。

（2）计算观测到的峰值的平均时刻：＾pα＝则估计出跳频信号的离散跳变时刻为：－。

跳频频率

（1）在估计出跳周期＾NH和跳变时刻＾na的基础上，求出在观测时间N内出现的完整频点数目i＝（符号“［］”表示取不大于符号内参数的最大整数）。

（2）跳频信号的重排谱图的峰值所对应的频率即跳频频率，即可得到跳频信号的跳变图案

4 仿真结果及性能分析

（1）时频分析的定量评价

文献 ［10］用信息熵来定量地评价时频分析的性能。信息熵用来描述事件发生的不确定程度，数学表达式为：式中，pi为事件的概率分布，K为一个常数。由式可知，当事件等概率分布时，此时信息熵最大，信息熵反映了概率分布的均匀性。在时频分布中，信息熵值越大即概率分布越均匀，说明其时频聚集性越差；同理，在聚集性相同的条件下，信息熵值越大说明交叉项干扰越大。因此，对于信号的时频分析，其信息熵越小，表示时频性能越好。表1给出了几种时频分布的信息熵。

表1 时频分布的信息熵

由表1可以看出，重排谱图与WVD和谱图相比，性能有显著的提高。

（2）参数估计性能

根据算法步骤，对2.4中的跳频信号 （信噪比为10dB，T＝0.05s）的谱图和重排谱图分别提取出其在每一时刻的最大值，即对图3和图4进行计算，得到图5和图6。

从图5和图6可知，经过时频分析后的最大值矢量具有周期性，由于对谱图进行了重排，导致了重排谱图的最大值曲线不平滑。对图5和图6进行傅里叶变换，得到图7和图8。

由图7和图8可知，最大值矢量的FT幅频图中最大的峰值所在的频率就是跳频信号的跳速。在信噪比为10dB的条件下，由图7得到的跳频信号的跳速为18.5547，即跳频周期T＝1／18.5547＝0.054s；由图8得到的跳频信号的跳速为19.5313，即跳频周期为T＝1／19.5313＝0.051s，由此可见，用重排谱图的方法对跳频周期的估计更加精确。由第三节参数估计的算法可知，跳变时刻的估计精度受到跳周期估计精度的直接影响，而对其估计的准确度又与跳频频率估计有关，因此，提高对跳周期的估计精度十分重要，文中仅对跳频周期 （跳频跳速的倒数）作性能分析。

图9为改变信号的信噪比，反复实验算法300次后对信号的跳频跳速估计的性能曲线图。由图可以看出，谱图对跳频跳速的估计相对误差在0.05～0.2之间，波动幅度较大；而重排谱图对跳频跳速的估计相对误差却精确到在0～0.1，精确度明显提高。

5 结束语

本文研究了重排谱图在跳频信号参数估计中的应用方法。通过对时频谱图的重排，提高了跳频信号在时频域内的聚集性，有效抑制了部分交叉项干扰，改善了时频图的可读性。针对跳频跳速 （跳频周期的倒数）的估计进行了性能仿真，仿真结果表明，与普通的谱图方法相比，重排谱图在低信噪比的条件下，提高了跳频周期及跳频频率估计的准确度。

图9 跳频跳速估计性能曲线

［1］ZHANG Wei，TANG Bin，ZHANG Jian.Ultra wideband highspeed frequency hopping signal reconnaissance technique ［J］.Telecommunication Engineering，2008，48 （4）：19－22 （in Chinese）.［张伟，唐斌，张健.超宽带快速跳频信号侦察技术［J］.电讯技术，2008，48 （4）：19－22.］

［2］GUO Jiantao.Ambiguity function of random frequency－hopping signals and its time－frequency analysis ［J］.Computer Engineering and Applications，2008，44 （18）：121－123 （in Chinese）.［郭建涛.随机跳频信号的模糊函数与时频分析 ［J］.计算机工程与应用，2008，44 （18）：121－123.］

［3］LU Yunsheng，DONG Yingying.Parameter estimation of frequency－hopping signals based on STFT ［J］.Ship Electronic Engineering，2011，31 （10）：73－74 （in Chinese）.［卢云 生，董英英.基于STFT的跳频信号参数估计 ［J］.舰船电子工程，2011，31 （10）：73－74.］

［4］LIU Yuzhen，ZHAO Ran.Frequency－hopping signal parameter estimation based on improved WVD ［J］.Computer Engineering and Design，2011，32 （11）：3616－3919 （in Chinese）.［刘玉珍，赵冉.基于改进WVD的跳频信号参数估计方法 ［J］.计算机工程与设计，2011，32 （11）：3616－3919.］

［5］CHEN Chao，HAO Yanzhong，GAO Xianjun.Parameter estimation of frequency－hopping signals based on amelioration algorithm of WVD ［J］.Journal of Jilin University （Information Science Edition），2010，28 （2）：124－130 （in Chinese）.［陈超，郝雁中，高宪军.基于 WVD改进算法的跳频信号参数估计 ［J］.吉林大学学报 （信息科学版），2010，28 （2）：124－130.］

［6］LU Hu，SHI Haoshan，XIE Yan.The estimation of FH signal parameter by multi－windows iterative SPWVD algorithm ［J］.Journal of Air Force Engineering University （Natural Science Edition），2008，9 （2）：52－55 （in Chinese）.［卢虎，史浩山，谢岩.估计跳频信号参数的多窗口迭代平滑伪WVD新算法［J］.空 军 工 程 大 学 学 报 （自 然 科 学 版），2008，9 （2）：52－55.］

［7］GUO Yi，ZHANG Eryang，SHEN Rongjun.The time－frequency analysis and blind parameter estimation of frequency hopping signals ［J］.Signal Processing，2007，23 （2）：210－213（in Chinese）.［郭艺，张尔扬，沈荣骏.跳频信号时－频域分析与参数盲估计方法 ［J］.信号处理，2007，23 （2）：210－213.］

［8］YAN Chaohui，TANG Jianlong.Hop duration estimation for frequency－hopping signals ［J］.Information and Electronic Engineering，2011，9 （1）：74－77 （in Chinese）.［严超会，汤建龙.跳频信号的跳周期估计 ［J］.信息与电子工程，2011，9（1）：74－77.］

［9］CHEN Lihu，ZHANG Eryang，SHEN Rongjun.Time－frequency analysis of frequency－hopping signals ［J］.Journal of Astronautics，2009，30 （2）：740－747 （in Chinese）.［陈利虎，张尔扬，沈荣骏.跳频信号的时频分析 ［J］.宇航学报，2009，30（2）：740－747.］

［10］ZHANG Xi，DU Xingmin，ZHU Liya.Blind parameters extraction of frequency－hopping signals based on reassignment SPWVD ［J］.Computer Engineering and Applications，2007，43 （15）：144－147 （in Chinese）.［张曦，杜兴民，朱礼亚.基于重排SPWVD的跳频信号参数提取方法 ［J］.计算机工程与应用，2007，43 （15）：144－147.］

［11］LEI Yingke，ZHONG Zifa，WU Yanhua.Hop duration estimation algorithm for high－speed frequency－hopping signals based on RSPWVD ［J］.Systems Engineering and Electronics，2008，30 （5）：803－805 （in Chinese）.［雷迎科，钟子法，吴彦华.基于RSPWVD高速跳频信号跳周期估计算法 ［J］.系统工程与电子技术，2008，30 （5）：803－805.］