基于真实能量衰减方程的水面特效模拟

庄甘霖，陈秀宏

（江南大学 数字媒体学院，江苏 无锡214122）

0 引 言

水面是现实世界里最常见的一种自然景观，也是必不可少的组成部分，真实水面的模拟对于增加虚拟自然环境的沉浸感可以起到非常重要的作用。水面模拟在游戏、影视、虚拟现实各领域中有着广泛的用途。作为自然景物模拟的重要内容，对流体、水面的模拟正日益引起人们的关注。从科学的角度来看，自然景物的真实感以及建模与绘制的实时性是其难点所在。由于水的形状是动态的、不固定的，且极不规则，因此不能用静态的几何多边形来表示；并且水面的光影效果取决于各种光线的反射和折射，它们的比例会根据视点位置的不同而不同，因此找到一种合适的模型来模拟真实效果并不容易。由于人们对视觉体验的要求不断提高，在实现大规模、高精度、绚丽特效的同时，高负荷的计算带来的时间与资源的消耗又对实时性提出了严峻的考验。近年来，基于波形分析的水面特效模拟在真实性与实时性上找到了一个不错的平衡点，得到了广泛的研究与应用。

随着计算机技术的发展，Max在1981年提出把整个水面作为高度场，通过正弦函数来模拟水面。在Max方法的启发下，越来越多的人开始研究将水波曲面作为一个参数曲面来处理，然后用波形函数来描述水波的外观形状和运动效果。Peachey在此基础上，使用了平面波方程，通过改变参数得到不同的水面效果。1986年Fournier和Reeves在波形函数中首次采用了Gerstner波函数。这种方法很好的解决了把波形作为高度场时，不能很好的表现激烈的水面环境的不足，使得算法的适用环境更加广泛。Perlin在文中还特别提到了模型的实际效果比它的物理意义更为重要。2001年，Tessendorf又对Gerstner波中的参数和叠加规律进行了深入的研究。童若锋借鉴了Peachey的算法，将水网格进行更进一步的细分，同时通过对水面网格的扰动操作，来产生逼真的水面微观效果，并且很好的解决了水面模拟不够光滑的问题。国内对于基于Gerstner波模拟海浪有着广泛的研究［1－3］。王海玲等［4］在2011年利用改进的曲面熵算法对水面进行动态分区，对不同区域施加不同程度的水面扰动，通过修正纹理映射位移的方法提高水面质感。对于水波模拟中GPU技术的应用，文［5－7］也各自做出了不错的效果。在能量衰减方面，陈和平等在2005年在算法中考虑增加了水波衰减效应的模拟功能，方法是将每次计算出的新振幅按一定的衰减率减小，因移位运算具有快捷性，衰减率选取1／16或1／32等。刘洁［8］等在模拟海浪时使用了线性衰减，波的振幅随着时间的变化衰减至0。黄玲［9］等则根据波浪理论使用了风速影响下的振幅A＝4.416＊10－3v2.5。2010年，侯学隆［10］等研究了基于方向谱的海浪合成方法，其中也根据波浪理论使用频谱得到了单元波振幅的变化。

以往的常见水体特效模拟中，往往对振幅采取线性衰减或者无衰减。线性与指数的衰减是凭经验、或者是适应计算来构造衰减方程，虽然渲染速度较快但是衰减不真实，并不能展现水波传播过程中真实的能量变化。基于波浪理论的振幅变化方程虽然有真实的数据指导，但其计算方法过于复杂，使得渲染速度下降，再者它来源于波浪，模拟常见水体时很难得到适当的波动效果。本文提出了一种基于Gerstner波模型的水面特效模拟方法。首先融入统计思想，针对单一Gerstner波波形变化较少的问题，采用三个Gerstner波进行叠加，寻找不同环境下合适的叠加方式；然后通过对水面真实波动过程的研究，得到水波传递时能量衰减的物理模型，引入能量衰减因子α，建立崭新的振幅随时间衰减的方程，将方程代入Gerstner波函数，使用新的模型来模拟水波；最后，引入反射率与透明度，对不同的环境与水体通过立方环境映射等技术，得到更好的光影效果，呈现出更真实的水面特效。

1 Gerstner波

捷克科学家Jozef Gerstner在1802年首次提出了精确描述任意幅度水波的模型，该模型描述了在水深比波长大的情况下表面波的摆线运动。模型中的偏移量由下列方程决定

公式中X0＝（x0，y0）是不受干扰的表面上的点，A是振幅，K是波矢，它是一个水平向量，方向为水波传播的方向，k是其大小，其取值与水波的波长有关

ω为水波的频率，取值将在之后讨论。

1986年，Fournier和Reeves将Gerstner波引入了计算机图形学，使用这个模型模拟水面上独立波动的点

式中：X ＝ （xt－1，yt－1）——该点上一时刻的水平面坐标值，Dx与Dy——单位波动向量K／k在x、y方向上的大小。当kA＜1时，波的形态是正常的，并且当kA越接近于1时，波峰更尖，波谷更平缓；当kA＞1时，在波峰上将会形成环，水波内部将会展示出来，达不到预期的真实效果。如图1所示。

图1 两个不同kA的Gerstner波

因此通过选取不同的振幅与波长可以得到尖锐程度不同的波形。

Gerstner波的波动特性有很大一部分取决于它的频率ω，根据流体动力学知识，波在水深为D的水体中传播时

当水体的深度与水波波长相近时，水体会对波的传播有更强的阻尼作用。通常情况下，当D＞λ／2时，由tanh函数的曲线接近于1，公式可简化为

从而有

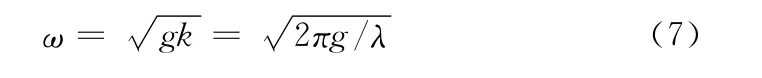
g为重力加速度，取为9.8 m／s2。

单一的Gerstner波无法满足对各种波形的需要，经实验分析，3个Gerstner波的叠加可以在效果和运算时间上得到很好的平衡

使用下面的公式得到叠加后水波各点的位置

从图2可以看出，选择合适的Gerstner波进行叠加，可以得到所需的各种波形。

图2 3个Gerstner波叠加效果

2 能量衰减

能量以波速在介质中伴随着波一起传播。单位时间内沿波速方向、垂直通过单位面积的平均能量称为能流密度，也称为波的强度，用I表示。能流密度是矢量，在各向同性均匀介质中，能流密度矢量方向与波速μ方向相同。水波的能流密度为

公式表明，水波的能流密度 （波的强度）大小与振幅A的平方成正比，与频率ω的平方成正比，与波速μ也成正比。

波在介质中传播时，介质总要吸收波的部分能量，因而波的强度将逐渐减弱，这种现象称为波的吸收。实验表明，当波通过距离为dx的介质薄层时，波的强度增量dI（dI＜0）正比于入射波的强度I与介质的距离dx，即

比例常数α是一个与介质的性质、温度及波的频率有关的量，称为介质的吸收系数，也就是波的能量衰减因子。积分后得

式 （13）中I0和I分别为t＝0和t＝t处波的强度。在模拟水波时，假设水波的传播速度μ＝1不变，则由式（11）与式 （13）可得振幅随时间衰减的函数

函数曲线如图3所示。

图3 振幅衰减函数曲线

将式 （14）代入式 （10）有

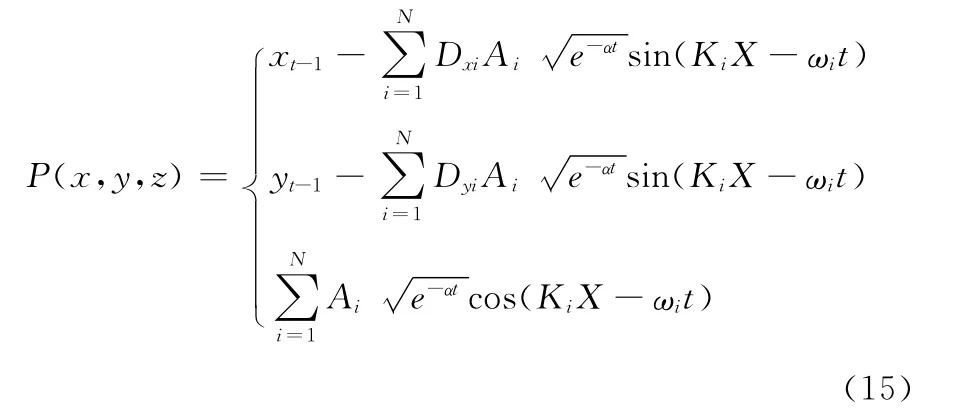
对比于式 （10），式 （15）将振幅随时间衰减的方程（式 （14））代入Gerstner波模型，使得在模拟水波时可以呈现出水波传播过程中能量的衰减，并且引入了衰减因子α，可以根据环境、水体的不同选择合适的α，得到更加真实的效果。

3 水面光影

3.1 立方环境映射

环境映射是一种常用的渲染反光表面的纹理映射技术。其基本原理是将反光物体所在的周边环境存储在称为环境图的纹理中。渲染物体时根据表面的反射向量到环境图中采样作为反射颜色。环境映射假定物体的尺度远远小于它与周边环境的距离，是一种近似的方法。但如果使用得当可以产生非常逼真的镜面反射效果。

立方环境映射是环境映射技术的一种，在三维图形渲染和游戏中得到广泛的使用。如图4所示，立方环境映射假想有一个巨大的立方体环绕在物体周围。物体所在的周边环境被映射到立方体的6个面上，然后存储为六幅纹理图像。这六幅纹理图像就构成了立方环境映射的环境图。纹理采样时假想从立方体中心发出一条沿反射向量R方向的射线，并计算该射线与立方体面的交点，然后根据相交面确定是六幅图像中的那一幅，再根据交点坐标在该图像中按照二维纹理的方式采样。

3.2 水面反射

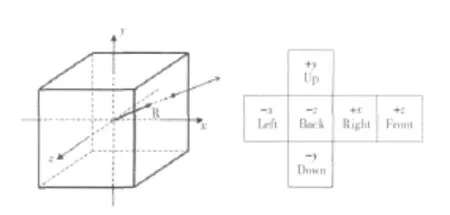
图4 立方环境映射

实现水面反射效果的一种常用方法是使用环境映射。如图5所示，P是水面上一点，N是P点处的单位法线向量，C是照相机 （观察者）的位置。

图5 水面反射效果的实现

首先计算从P指向照相机的单位向量V

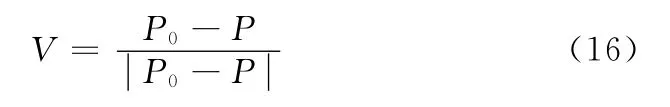
然后计算V相对于法线N的反射向量R

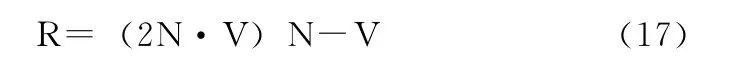
R与反射纹理平面的交点D

由于

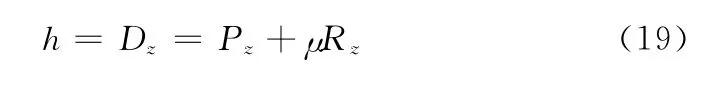
所以

使用D作为纹理坐标到反射平面中采样得到P点处的反射颜色。

3.3 水面折射

图6中，d为水面到水底的平均深度，ηi与ηr分别为空气与水的折射率，θi与θr分别为折射光 （入射光）与界面法线的夹角，由斯涅耳定律可知

则折射向量

将其单位化有

T与折射纹理平面的交点E

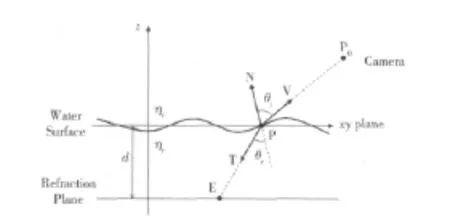
图6 水面折射效果的实现

由于

所以

使用E作为纹理坐标到折射平面中采样得到P点处的折射颜色。

3.4 颜色融合

在得到P点的反射颜色Creflect与折射颜色Crefract后，通过下面的公式得到P点的最终颜色：

式中：Cambient、Cspecular与Cdiffuse——环境光、镜面反射光与漫反射光，fspecular与fdiffuse——镜面反射系数与漫反射系数。r与t——水面的反射率与透明度，根据不同环境下的不同水体，调节r与t可以得到理想的水面光影。

4 实验结果及分析

根据以上方法，模拟水面特效。采用 Windows XP平台下的Visual C＋＋6.0和OpenGL 2.0进行绘制。硬件平台为 Pentium Dual－Core E6700 3.2GHz，2GDDR3－1333内存，显卡为 ATI Radeon HD 4350。

图7为模拟结果，其中图7 （a）、图7 （b）、图7（d）分别为衰减因子α为0.01时，时刻t分别为1秒、100秒和250秒时的场景截图。图7（c）、图7（e）分别为线性衰减时刻t分别为100秒和250秒时的场景截图。反射率为0.8、透明度为0.2。

从模拟结果来看，振幅的线性衰减过程是均匀过度的，显得较为生涩，真实能量的衰减则较为柔和，更加自然。配合新的能量源产生的波形，便可得到理想的水面波动效果。在1440×900的分辨率下，渲染帧数达到了224帧每秒，可以满足各种游戏和动画场景的需要。

5 结束语

本文通过对真实水波物理特性的研究，得到了崭新的水波传播时能量衰减的方程。将其带入Gerstner波模型模拟水波，使用反射率与透明度控制光影效果，得到了更加真实的水面特效以及不错的渲染速度。而且此方法简单，适用性强，在多种软、硬件平台下都得到了理想的效果，有很强的通用性。

图7 真实能量衰减与线性衰减的比较

下一步的工作重心将会放在水面刻蚀等光学效果以及浪花、涟漪等物理过程的研究。并进一步挖掘GPU的潜能，提高渲染速度。

：

［1］LI Sujun，YANG Bing，WU Lingda.Modeling and rendering of ocean scene based on Gerstner－Rankine model ［J］.Journal of Engineering Graphics，2008，29 （2）：77－82 （in Chinese）. ［李苏军，杨冰，吴玲达.基于Gerstner－Rankine模型的真实感海洋场景建模与绘制 ［J］.工程图形学报，2008，29 （2）：77－82.］

［2］FENG Kaiping，LIU Tao.Research on wave real－time simulation based on 3DGerstner wave ［J］.Journal of Engineering Graphics，2009，30 （5）：52－57 （in Chinese）. ［冯开平，刘涛.基于3DGerstner水波的实时模拟研究 ［J］.工程图形学报2009，30 （5）：52－57.］

［3］HUANG Wei，WANG Changbo，XIE Buying.Real－time rendering of overturning waves based on Gerstner－wave model ［J］.Journal of University of Shanghai for Science and Technology，2009，31 （1）：72－76 （in Chinese）.［黄威，王长波，谢步瀛.基于Gerstner波模型的海洋卷浪实时仿真 ［J］.上海理工大学学报，2009，31 （1）：72－76.］

［4］WANG Hailing，YIN Guisheng，ZHANG Jing，et al.Dynamic water surface simulation method based on improved surface entropy ［J］.Computer Engineering，2011，37 （6）：24－26 （in Chinese）.［王海玲，印桂生，张菁，等.基于改进曲面熵的动态水面模拟方法 ［J］.计算机工程，2011，37 （6）：24－26.］

［5］LI Sujun，YANG Bing，GAO Yu，et al.GPU－based real－time rendering of large－scale ocean wave ［J］.Computer Simulation，2008，25 （5）：190－194 （in Chinese）.［李苏军，杨冰，高宇，等.基于GPU的大规模海浪实时绘制 ［J］.计算机仿真，2008，25 （5）：190－194.］

［6］GUO Xingzhao，ZHANG Jun.Simulation of water based on GPU ［J］.Computer Simulation，2010，27 （1）：218－221 （in Chinese）.［郭新钊，张军.基于图形处理器的水面仿真 ［J］.计算机仿真，2010，27 （1）：218－221.］

［7］LIU Xiaoping，XIE Wenjun.Research on the method of simulation of real－time water surface based on GPU ［J］.Journal of Graphics，2010，31 （1）：79－83 （in Chinese）.［刘晓平，谢文军.实时水面模拟方法研究 ［J］.工程图学学报，2010，31（1）：79－83.］

［8］LIU Jie，ZOU Beiji，ZHOU Jieqiong，et al.Modeling gerstner waves based on the ocean wave spectrum ［J］.Computer Engineering and Science，2006，28 （2）：41－44 （in Chinese）.［刘洁，邹北骥，周洁琼，等.基于海浪谱的Gerstner波浪模拟［J］.计算机工程与科学，2006，28 （2）：41－44.］

［9］HUANG Ling，WANG Changbo，YANG Bo，et al.Photo－realistic modeling and rendering of curved wave ［J］.Computer Engineering and Applications，2009，45 （32）：164－167 （in Chinese）.［黄玲，王长波，杨波，等.卷浪的真实感建模与绘制 ［J］.计算机工程与应用，2009，45 （32）：164－167.］

［10］HOU Xuelong，SHEN Peizhi，WANG Wenyun.Method of ocean wave synthesis based on directional spectrum ［J］.Journal of System Simulation，2010，22 （1）：130－134 （in Chinese）.［侯学隆，沈培志，王文恽.基于方向谱的海浪合成方法 ［J］.系统仿真学报，2010，22 （1）：130－134.］