组合近似重分析算法中迭代终止性判定与基向量的自适应分析
王学强
(同济大学建筑工程系,上海 200092)
组合近似重分析算法中迭代终止性判定与基向量的自适应分析
王学强
(同济大学建筑工程系,上海 200092)
本文简要介绍了结构重分析算法及其在结构优化中重要作用。针对基于空间网格结构优化的组合近似重分析算法,结合误差范数的概念,实现了CA算法中迭代过程终止性判定与基向量数目的自适应选定,并对精确性、收敛性及效率进行了分析与讨论。
组合近似算法(CA);结构重分析;收敛性;误差估计
引言
目前,国内对利用计算机进行方案阶段的概念设计方面进行了一些尝试,并构建了基于性能的结构生(合)成理论。该理论由结构形状语法、结构分析与评估、结构优化技术三者组合而成[1,4]。
一般来讲,结构优化问题可分为尺寸优化、几何优化及拓扑优化三大类别,均涉及平衡方程的求解:直接法(精确解)和近似法(数值解)。对于大型结构,反复精确求解则包含大量数学运算(主要为矩阵求逆),效率势必较低。虽然一定精度的近似解即可满足工程需要,而求解近似解的利器则是利用结构重分析技术。
一个典型的重分析过程如下所示:
假定某一初始设计对应的刚度矩阵为K0,求解平衡方程(K0r0=R0)得初始位移r0:
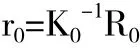
假定结构发生某种变化DK,则刚度矩阵K=K0+DK,平衡方程变为:
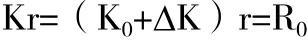
重分析的目标即是尽量避免矩阵求逆而高效求解由于结构变化后的位移r:
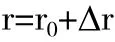
复杂空间网络结构数字化生成与优化过程中需进行大量新结构的生成、分析与评估,新结构由上一结构变换个别杆件尺寸、或局部坐标位置、或局部拓扑得到;若每次对新结构进行完整分析将耗费大量机时(约为85%的运行时间),而利用结构重分析技术,新结构的内力变形解等于上一结构的内力变形解“加”上一个“修正量”得到,避免了矩阵求逆等复杂计算,大大加快了优化运算的速度[1]。
1 组合近似重分析算法简述
一般来讲,不同重分析算法其精度和效率不尽相同,算法选取需综合考虑精度、效率和可行性等因素。结构重分析算法的直接法[6,7]主要基于Woodbury公式和Sherman-Morrison 公式;近似重分析算法可分局部单点近似、合局多点近似和组合近似(Combined Approximation,以下简称CA法)等。
CA法最初由Kirsch[2]提出,系将将全局近似(缩减基底法,RB)结果质量精度高的特性赋予具有较高计算效率的局部近似(二项式级数展开法,BSA)。在CA法中,二项式级数展开式中前若干经过计算的项被运用于简化基表达式中的基向量,从而获得一个有效的求解过程,而基向量的未知系数可通过求解一个简化方程组而得到。
CA法起初多用于小型结构;研究表明,在大型结构设计当中,即使结构变动较大,运用CA法亦能得到较好的近似结果[2]。对于不同类型的结构或者设计变量,如桁架、框架或网架中的截面、几何变化或拓扑变动等,CA法均适用。
2 CA法的范数误差公式
Kirsch等研究表明[2],引入Gram-Schmidt正交化后,CA法的精度和效率可进一步提高,且生成的正交基向量可使缩减方程解耦:不仅可避免非线性分析过程中可能遇到病态矩阵情况,还可将结构位移以显式方式精确表达,从而可以控制算法的效率和精度(即若需提高近似精度,可在原有计算结果的基础上进行“修正”而无须重新完整计算),保证了算法的高效性与鲁棒性。结构优化重分析一般涉及三种类型的收敛性情形:级数收敛快、级数收敛慢、级数发散,对此CA法均能求得相当精确的解。
利用CA法中正交基向量的特点,本文采用如下误差范数[3]公式用以判断收敛性并实现基向量数目的自适应选择。
‖·‖——欧几里得范数;
r——位移向量;
Vi——第i个正交基向量;
S——所选取的基向量个数。
3 数值模型分析
3.1 计算初始结构模型
以图1所示模型研究CA法的基向量数量与指定精度之间的关系——即利用误差 范数的概念研究判断何时终止CA法的迭代过程,实现基向量数目的自适应选定。本文主要研究以下几种情况:
用相邻向量之间变化进行判断;用新增基向量占基向量总和的比例进行判断;用单个位移的相对误差进行判断;利用误差范数进行判断。
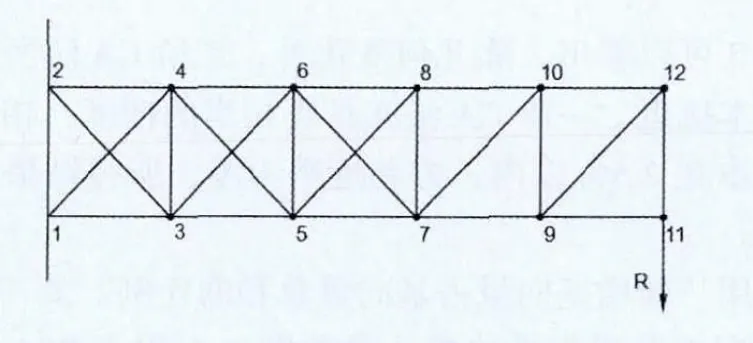
图1 初始结构
3.2 数值算例分析
3.2.1 用相邻基向量之间的变化进行判断
假设结构中杆件4-6截面积减小50%,运用CA法计算不同数目基向量下的位移,见表1。
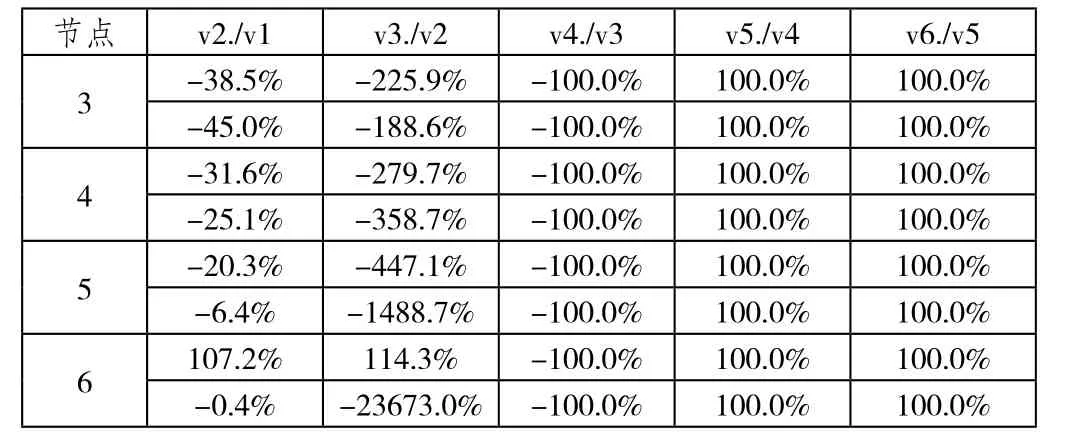
表2 相邻基向量对应比较
表2显示,对于单根杆件截面尺寸变化,从第4个基向量(三阶CA法)开始,基向量保持恒定;当基向量数超出某个值或值域后,计算精度开始恶化,即CA法的计算精度与基向量数目呈抛物线变化关系——当基向量的个数仅在某个特定值或值域内时所求结果精度较高。对于本例当相邻基向量之间比值为1时,CA法即可终止计算,此时基向量个数应为出现比值1前的数量;但该种判断方法属于“后验”法——即需先求出后续基向量后方能判断是否采纳该基向量。
3.2.2 用误差范数公式进行判断
在重分析计算过程中,收敛准则的选取应满足一定原则:计算量小且能在执行下一轮计算前判断出是否需增加基向量,即应具有“先验性”:误差范数公式可实现在本轮计算结束时根据限定精度(ErU)判断出是否有必要进行下一轮计算而不必先计算一个新规则化的基向量,从而提高了计算效率,加速收敛。
表3给出了空间网格结构优化过程中涉及的基本变化类型及采用误差范数判断达到限定精度所需的正交基向量数目。
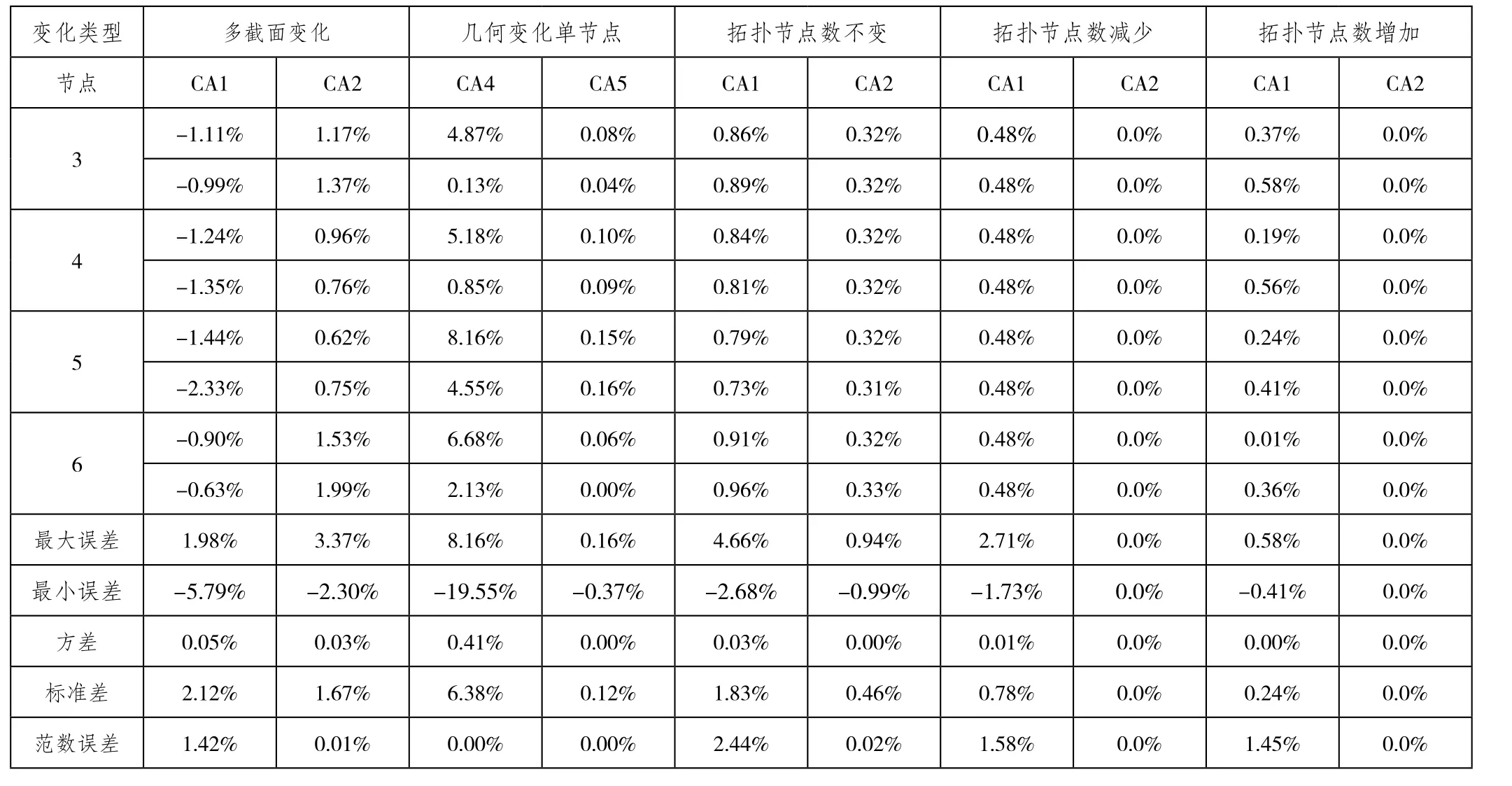
表3 引入范数误差判断不同类型结构优化CA法基向量数目选取分析
从表3可以看出,除几何变化外,二阶CA法所得结果与精确值基本接近,一阶CA法亦具有相当的精度:相对误差的标准差基本在2.5%以内,方差近乎为零,所得结果具有较高的置信度。
而利用“新增基向量占基向量总和的比例”及“用单个位移的相对误差”进行迭代终止性判断,多用于BSA法中,均属于“后验性”方法,且数值稳定性较差,不予深入讨论。
4 引入误差范数判断的CA法算法效率分析
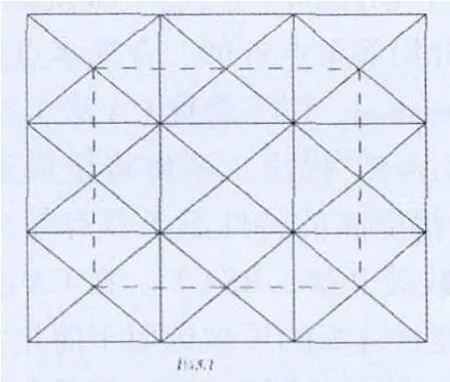
图2 空间网格结构
以某一空间正放四角锥网架[5](见图2)的优化过程为例。分析引入误差范数后的CA法优化程序的计算效率。
该网架平面尺寸为12m×12m,四角采用点支承(作铰接点处理)。初始截面尺寸均为100mm2,E=2.06×105MPa,下层节点竖向荷载为R=100kN。
运用不同阶数CA法达到最优结构所需计算时间见表4。

表4 计算时间对比
可以看出,CA法的引入提高了优化过程中重分析环节的执行效率,且引入误差范数后根据精度要求可实现CA法迭代终止性判断与基向量数量的自适应性选定。如限定计算精度为2%,仅需计算3个基向量(二阶CA法),相对于三阶CA和完整解法,计算时间分别为两者的71.48%、26.97%。
数值算例表明,利用范数误差计算位移的相对误差并用以判断何时结束CA法的迭代过程实现了CA法基向量数目的自适应性选定。
[1]赵宪忠.S.Kristina.空间杆系结构的智能生成与设计[N].建筑结构学报,2010.
[2]王仁华.基于形状语法的空间网格结构优化.上海.同济大学,2010.
[3]王帅.基于模拟退火和结构重分析的网架结构优化设计.上海.同济大学,2007.
TP273
A
1671-3362(2013)07-0113-02

