基于轮胎磨损的悬架与转向系统硬点优化*

唐应时，朱位宇，朱 彪，孙鹏飞，干年妃

(1.湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082; 2.一汽大众汽车有限公司，长春 130000;3.厦门理工学院机械工程系，厦门 361024)

前言

汽车轮胎与悬架共同作用缓解路面冲击，支撑车辆质量，保证车轮与路面的良好附着能力。轮胎磨损会严重影响轮胎性能。文献［1］和文献［2］中基于刷子模型分析了轮胎侧偏、纵滑和侧偏纵滑模型3种工况下轮胎磨损机理，文献［3］中从车轮横向拖移量的角度分析前轮定位参数中前束角与外倾角的配合关系。文献［4］中考虑到转向系统对前束的影响从转向阿克曼角度方向优化转向系统的硬点坐标。由于在悬架跳动时，悬架运动瞬心与转向拉杆瞬心不重合，会影响跳动过程中前束角的变化趋势与范围［5］。本文中从轮胎磨损机理上分析悬架与转向系统设计要求，整体上对悬架和转向硬点一同优化，并且考虑到轮胎在整个跳动过程中前束与外倾的匹配关系，有效减轻轮胎磨损，减少干涉现象的出现。

1 悬架与转向系统匹配设计要求

汽车转向系统与悬架匹配设计时主要考虑［6］:(1)当车轮上下跳动时，转向杆系与悬架的运动干涉所引起的车辆前束角变化要尽量小;(2)车辆转向行驶时，机构所引起的干涉要有利于不足转向的产生。双横臂悬架与独立式转向梯形结构布置时指导思想是:转向节臂与转向连杆连接的球铰中心的瞬心与断开点中心重合。如图1所示，EC代表上横臂，GD代表下横臂，UT为转向拉杆，P点为瞬心交点，M为转向节臂与主销交点为转向拉杆瞬心运动曲线为双横臂瞬心运动曲线。

根据设计要求，悬架的跳动瞬心与转向拉杆的跳动瞬心在空间运动过程中尽量重合，即图1中的阴影部分的面积越小，则由悬架与转向系统匹配带来的轮胎磨损越少。在车轮行驶过程中，由于跳动带来的轮胎磨损、直线行驶能力与悬架及转向硬点关系密切。因此在设计悬架系统时，必须考虑到转向系统的布置。只有考虑到整个跳动过程中的前轮定位参数变化和转向阿克曼角度误差，才能有效减轻轮胎磨损，提高操作稳定性。

2 前轮定位参数与轮胎磨损的关系

在汽车行驶过程中，主销参数内倾角和后倾角不是直接体现轮胎空间姿态的参数，所以本文中主要从前束角和外倾角考虑其对轮胎磨损的影响。对基于刷子模型的轮胎侧偏纵滑工况进行磨损分析，从前轮定位参数、阿克曼误差与轮胎侧偏角关系进行轮胎磨损量分析。

2.1 车轮外倾角对轮胎磨损的影响

外倾角对于轮胎磨损和汽车操作稳定性都有一定影响。当车轮在一定的外倾角下滚动时，将会产生一定侧倾力，等效为车轮产生了侧偏角Δα。轮胎磨损的实质是地面对轮胎做功，当做功超过轮胎承受能力时，便产生了轮胎磨损。因此可用轮胎做功的大小来表示车轮侧偏角与轮胎磨损的关系［1-2，7-8］，磨损功为

式中:Wx为侧向力所做摩擦功;Wy为纵向力所做摩擦功;a为轮胎接地印迹长的一半;u为轮胎接地处的坐标变量;uc为轮胎起滑点;qz(u)表示为轮胎载荷分布;μx、μy分别为侧向与纵向车轮附着系数;y't(u)代表轮胎侧向变形曲线;Sx为纵向滑移率。

2.1.1 轮胎接地印迹长度计算

本文中采用165/70R13LT子午线轮胎。根据吉林工业大学推荐的经验公式计算轮胎接地印迹长度［8］为

式中:m=0.576，为子午线轮胎经验指数;D为轮胎名义外径;Δ为轮胎在垂直载荷下的径向变形量，由匈牙利学者科曼第推荐公式［8］确定:

式中:C=1.5为子午线轮胎修正系数;K=0.0015b+0.42，为修正系数;b为轮胎断面宽度，cm;Wn为轮胎垂向载荷，N;p为胎压，0.1MPa。

计算得轮胎印迹长度为162.04mm。

2.1.2 轮胎平均接地压力分布计算

考虑在标准载荷下，简化选取对轮胎影响较大的印迹纵向中心线上的压力分布来表示轮胎平均压力。根据日本学者Sakai提出的轮胎在纵向的接地压力分布为

式中:n为指数系数，子午线轮胎n可近似为4;x为轮胎接地点坐标;b0为接地印迹宽度。

得到印迹纵向中心线上压力分布如图2所示。则计算得到外倾角对轮胎磨损的影响如图3所示。

2.2 车轮前束角对轮胎磨损的影响

由于存在外倾角，车轮直线行驶时会出现圆锥摆运动，所以使用前束消除外倾角带来的负面影响。根据前束角的定义，其可以视为小角度下车轮的侧偏角。用式(1)～式(3)计算得到前束角对轮胎磨损的影响，如图4所示。

由图3和图4可得在稳态侧偏纵滑工况下，车辆直线行驶时，由前束角带来的轮胎磨损远比外倾角带来的磨损严重。

2.3 阿克曼误差对轮胎磨损的影响

阿克曼误差是指理论阿克曼转角值与实际车轮转角的差值。由于阿克曼误差存在，造成轮胎拖滑。根据车轮侧偏角的定义，阿克曼误差实际上可视为附加于该轮上的侧偏角，且大小等于前束角的一半。其对轮胎磨损的影响如图5所示。

由上可知，由前束带来的轮胎磨损大于外倾角造成的磨损;阿克曼误差造成的轮胎磨损为前束所造成的轮胎磨损量的一半，但常用转角下，阿克曼误差的变化量较小，因此由其所造成的轮胎磨损量也较小。

3 车轮跳动过程中实验设计和变量选取

悬架与转向系统的空间运动状态难以用精确的数学模型来表达，因此只能从数学统计和拟合角度，利用RSM(response surface method)法拟合出悬架与转向系统运动状态的函数关系。

为减少计算量，提高工程可行性，首先在Adams/Car中建立某车型的前悬架转向系统虚拟样机模型，选取车轮上、下跳极限、中间位置3种工况的外倾角和前束角作为实验设计对象，利用Insight模块对硬点坐标进行灵敏度分析［4，9-10］。

3.1 前悬架系统虚拟样机模型的建立

某车型前悬架为双横臂扭杆式独立悬架，使用传统机械式齿轮齿条转向器，断开式转向梯形。轴荷分配为50%～50%。根据满载硬点坐标建立如图6所示的虚拟样机模型。调整模型整车参数和前轮定位参数如表1所示。

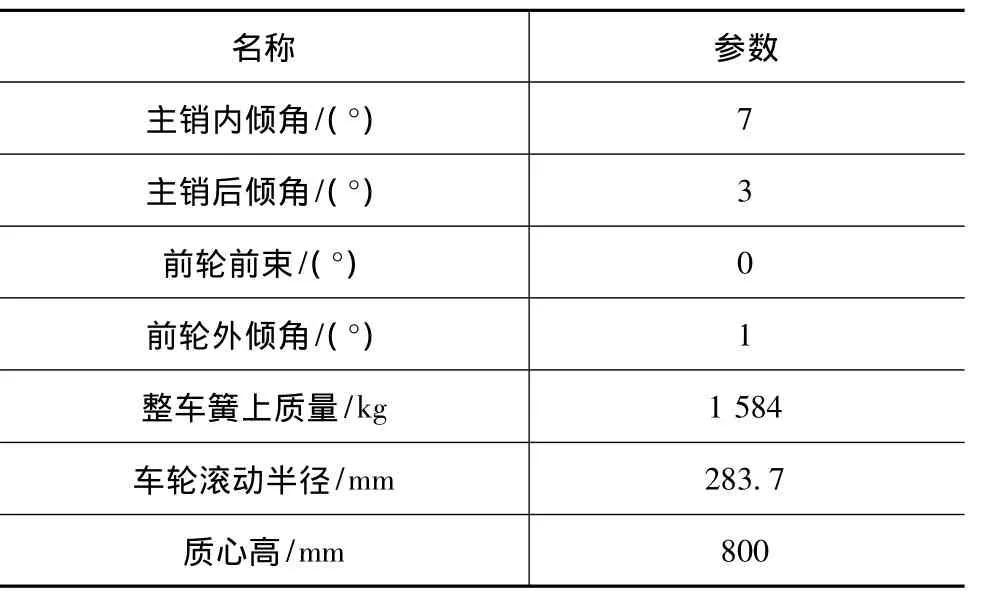
表1 部分整车参数

3.2 主要硬点变量灵敏度分析

在Adams/Insight模块中分别以车轮外倾角和前束角变化为目标函数，对所有硬点坐标运用实验设计进行变量分析，得到如表2和表3所示的变量灵敏度(表格中主要选取灵敏度变化大于15%的变量予以列出)。

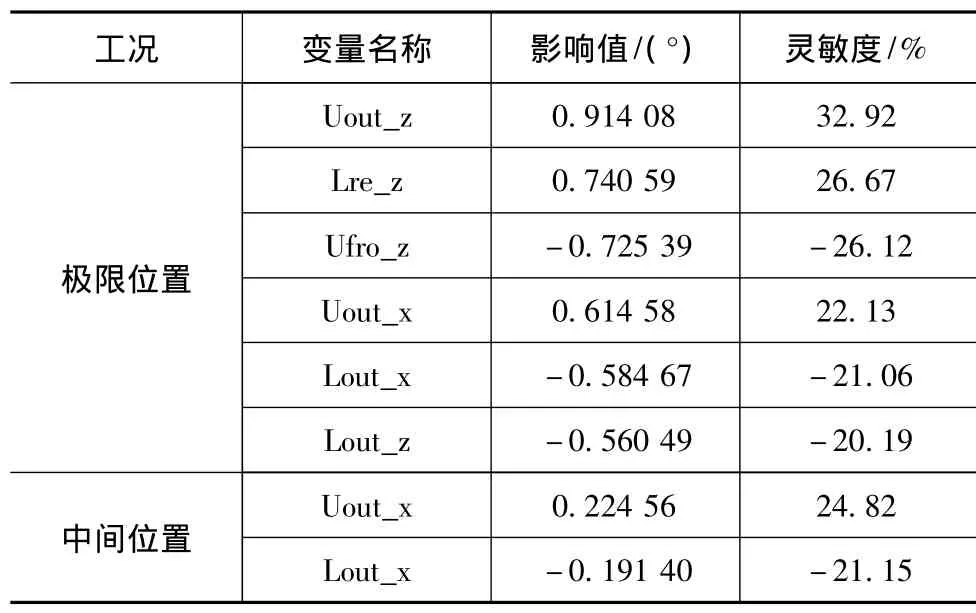
表2 硬点变量对外倾角的影响

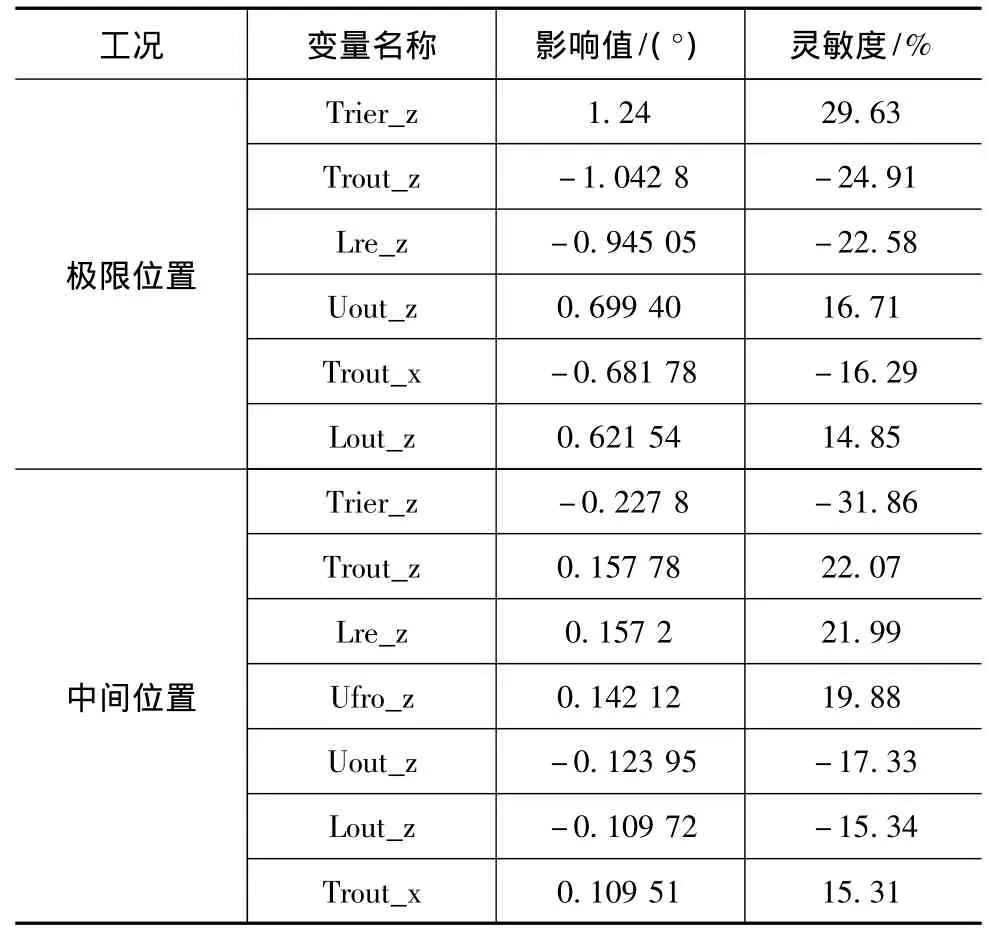
表3 硬点变量对前束角的影响

表2和表3中正的灵敏度表示目标值函数随变量变大而增长，负的灵敏度表示目标值随变量变大而减小。

3.3 优化变量的选择

由表2和表3可得，在整个跳动过程中转向拉杆内、外球头坐标点的Trier_z、Trout_z坐标对于前束的影响较大;而上下横臂的前、后硬点的Uout_x，Lout_x，Uout_z，Lre_z，Ufro_z，Lout_z 坐标对外倾角影响较大。转向外球头Trout_x坐标对转向阿克曼误差影响较大［4］。因此选取上下横臂点、转向拉杆内外球头点上述坐标作为优化变量，设置9个变量，写成矩阵形式为

4 目标函数的响应面法拟合

选取上述9个灵敏度较高的变量拟合复杂工况下的前束角和外倾角，中间位置的后倾角和转向工况下的阿克曼误差8个响应面输出函数。响应面函数为

式中:α 为常数项;B=［βi］T，其中 βi为一次项系数;C=［γij］n×n为二次项系数矩阵;γij为二次项系数，i，j=1，…，n;n为变量个数。

4.1 上跳极限位置外倾角响应面函数

选取下横臂后点Z坐标、下横臂外点Z坐标，上横臂前点Z坐标，上横臂外点X坐标和上横臂外点Z坐标这5个影响因子较大的变量来拟合车轮上跳极限外倾角目标函数。拟合函数采用二次函数，研究策略采用DOE Response Surface，设计类型为全变量设计［10］。拟合结果为

经检验多重相关系数R2为0.993 452，多重样本相关修正系数为R2adj为0.991 599，说明该拟合函数可以较好地描述目标函数。

4.2 其它目标的响应面函数拟合

同样选择不同变量运用Insight模块拟合出车轮上跳极限位置的前束角响应面函数为Ts;下跳极限位置的前束角响应面函数为Te，外倾角响应面函数为Ce;车轮中间位置时的前束角和外倾角响应面函数为Tm，Cm;以及中间位置的转向工况下的阿克曼误差响应面函数为Km和中间位置后倾角响应面函数Ctm。上述函数的具体计算过程和结果予以省略，方法同4.1节所述。

5 优化过程描述

5.1 约束条件设置

在车轮单向跳动过程中，车轮外倾角、前束角和主销后倾角均呈现单调变化的趋势。要求外倾角、前束角随车轮上跳而减少，以提高轮胎附着能力，增大不足转向倾向。在优化车轮外倾角和前束角时，部分坐标对于主销后倾角的影响较为明显，因此须同时约束主销后倾角的变化范围和趋势。

具体约束函数为

5.2 目标函数确定

根据轮胎磨损机理和前束角、外倾角及阿克曼误差对轮胎磨损影响的分析，可知轮胎侧偏角变化越小，则轮胎磨损越小。因此目标函数为轮胎磨损量最小，即要求前束角、外倾角和阿克曼误差的变化尽量小。具体函数式为

5.3 优化结果

利用Matlab多目标优化工具箱得到新的硬点坐标，并带入Adams/Car中施加上下跳动距离为50mm，进行平行轮跳和中间位置转向工况仿真。

外倾角与车轮垂向位移关系的优化前后对比见图7。前束角与车轮垂向位移关系的优化前后对比见图8。左轮阿克曼误差与左轮转角关系的优化前后对比见图9。

由图7和图8可知，车轮外倾角和前束角都随车轮上跳而减小;外倾角变化范围由原来的［-1.9°，2.8°］变为［-1.8°，1.6°］，整个范围减小了27.65%;改变原前束角曲线变化趋势，使之更加符合设计要求;由图9可知，在0°～25°常用角度范围内，阿克曼的均方根值减小了14.7%，可认为转向梯形机构设计更为合理。同时，在整个跳动过程中外倾角和前束角的匹配范围更大，较大地减轻了轮胎磨损。

6 结论

(1)基于轮胎刷子模型分析稳态侧偏纵滑模型，定量分析前轮定位参数和阿克曼误差对轮胎磨损的影响，发现前束角对轮胎磨损有较大影响。

(2)经过优化，车轮外倾角变化范围减小27.65%;前束角随车轮上跳时的变化量减小，符合设计要求;常用转角状态下，阿克曼误差均方根值减小14.7%。

(3)将悬架系统与转向系统同时优化，符合汽车设计理念，有效减小悬架与转向系统的干涉量，避免传统单一目标优化的片面性，从而有效减轻轮胎磨损，延长轮胎寿命。

［1］ 刘青，郭孔辉，陈秉聪.轮胎刷子模型分析I稳态侧偏刷子模型［J］.农业机械学报，2000，31(1):19-22.

［2］ 刘青，郭孔辉，陈秉聪.轮胎刷子模型分析II稳态侧偏刷子模型［J］.农业机械学报，2000，31(2):129-134.

［3］ 魏道高，陈雪琴，胡能俊，等.车辆前轮前束值与外倾角合理匹配算法的商讨［J］.农业工程学报，2003，19(6):139-142.

［4］ 周兵，杨凡，徐琪.基于ADAMS的转向机构的优化设计［J］.湖南大学学报，2008，35(12):23-26.

［5］ 王宵锋.汽车底盘设计［M］.北京:清华大学出版社，2010:388-394.

［6］ Joško Deura，Jahan Asgari，Davor Hrovat.A 3D Brush-type Dynamic Tire Friction Model［J］.Vehicle System Dynamics，2004，42(3):133-173.

［7］ 郭孔辉，吴海东，卢荡.冰面上轮胎稳态侧偏刷子模型［J］.吉林大学学报(工学版)，2007，32(7):253-258.

［8］ 庄继德.计算汽车地面力学［M］.北京:机械工业出版社，2001:53-59.

［9］ 丁飞，韩旭，等.悬架导向机构硬点灵敏度分析及多目标优化设计［J］.汽车工程，2010，32(2):138-142.

［10］ 李伟平，王世东，周兵，等.基于响应面法和NSGA-Ⅱ算法的麦弗逊悬架优化［J］.湖南大学学报(自然科学版)，2011，38(26):28-32.