振弦式应变计数学模型的比较分析

李 滨 钟文斌 林飞振 / 广州计量检测技术研究院

0 引言

振弦式传感器是目前国内外普遍重视和广泛应用的一种非电量电测的传感器。由于振弦式传感器直接输出的是自振频率信号，不会因导线电阻的变化、温度波动的变化而引起信号的明显衰减，具有性能稳定、抗干扰能力强、零点漂移小、耐震和寿命长等特点，因此受到工程界的广泛关注。到20世纪70年代，随着现代电子技术、材料和制造工艺技术的进步，振弦式传感器技术得到了完善并真正能满足工程应用的要求。近年来已被大量运用于大坝[1-2]、隧道[3]、矿井[4]、道路桥梁[5]、地基基础[6]、船舶应力[7]等的受力状况的测试和长期监测，有着十分广阔的应用和发展前景。

振弦式传感器的精度直接影响测试的数据是否准确、可靠进而影响工程的质量和安全。其精度的高低不仅与材料和制作工艺有关，还与其采用的数学模型有着重要的关系，王学水、白泰礼、于凤等人[8-11]对振弦式传感器都提出了相同的数学模型，并对这一模型进行了验证，使振弦式传感器的拟合精度得到提高。国内外的一些学者也提出了一些其他的数学模型来提高振弦式传感器的拟合精度。

本文根据国内外的资料总结归纳了几种振弦式传感器的数学模型，以振弦式应变计测量得到的试验数据，分析比较各数学模型及其计算方法优缺点和对振弦式应变计拟合精度的影响，为振弦式应变计拟合精度的提高提供借鉴。

1 振弦式应变计的工作原理

主要有单线圈激励方式（间歇触发激振）和双线圈激励方式（等幅连续激振）。单线圈激励方式的工作原理是激励线圈既激励弦产生振动也接收弦的振动所产生的激励信号，双线圈激励方式是一个线圈激励，一个线圈接收。除了线圈外，传感器还带有一个热敏电阻，用以测试传感器周围环境温度，以便进行温度修正（见图1）。

图1 振弦式应变计

一根钢丝弦固定在具有保护和支撑作用的应变筒内，此时钢丝弦具有一定的固有频率。把振弦式应变计固定在结构物的表面或内部。当结构物内部的应力发生变化时，钢丝弦与应变筒同步感受结构物的变形，钢丝弦的应力发生变化，固有频率随之变化。通过测试弦的固有振动频率就可以确定其内部张力的变化（与结构应变相关联），通过测量钢丝弦固有频率的变化，就可以测出结构物应变，振弦式应变计就是根据这一原理制成的。由振动理论得知其钢丝弦固有频率与所受应力之间的关系可表示为

式中；f — 钢丝弦的自振频率；

σ — 钢丝内部拉或压应力；

L — 钢丝弦长度；

ρ — 钢丝弦线密度(单位长度的质量)

由（1）式可以得到

式中：k = 4ρL2；

f0：初始频率，Hz；f：当前频率，Hz；

σ0：初始应力，MPa；σ：当前应力，MPa

由于振弦式应变传感器的应变筒与其中钢丝弦变形协调，应变增( 减)量相同。设应变筒的应变增量为εh，钢丝弦的应变增量为εg，

2 数学模型

2.1 模型一

式（3）是国标GB/T 3408.2-2008《大坝监测仪器应变计》中采用的一般计算模型（在不考虑温度的影响下）。国内生产振弦式应变传感器的厂家在其出厂检验报告中也都一直使用这个模型来计算应变量。其标定系数K值的确定有以下三种方法。

1）总量均值法

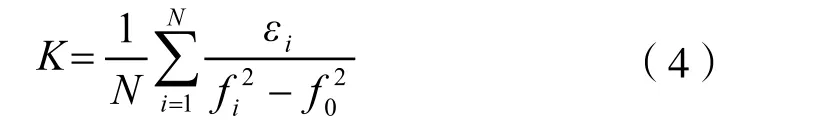
2）增量均值法

3）最小二乘法

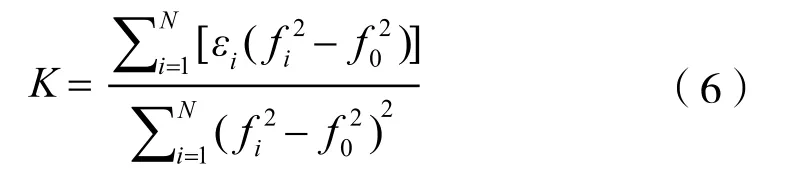
2.2 模型二

假设给定一组标定用数据 {εi，fi} i=1，2，3，…，N。可用多种数学式进行拟合。例如：多项式、牛顿插值多项式、以及三次插值样条函数等。从振弦式应变计原理推导的模型计算式（3）中可以看出，应变量与频率是二次项关系，故可假设为标准的二次抛物线模型：

其中，系数a、b、c可以由相应的计算软件直接得出。

2.3 模型三

王学水、白泰礼等人从振弦式传感器的原理出发，提出了一个新颖的振弦式传感器数学模型：

其中系数A、B可由最小二乘法确定

2.4 模型四

国外的一些技术资料中采用多项式回归衰减的方法来计算变化量[12]，

其中系数α、β由以下两式给出

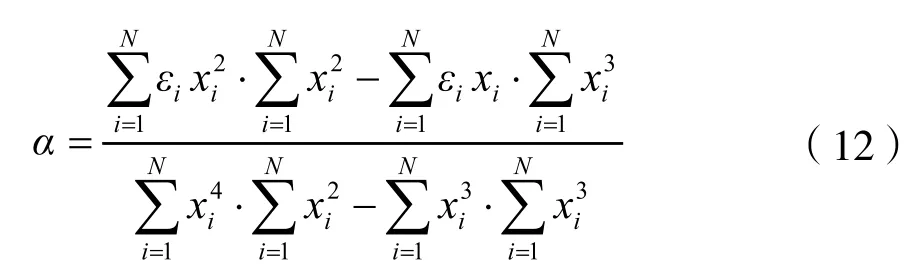
3 计算分析

本文以澳大利亚生产的振弦式应变计（1#）为例，对其进行标定得到一组试验数据（见表1），利用该数据分别对上述四个模型和计算公式进行比较分析，得到各个数学模型和计算公式的拟合精度误差曲线图（见图2）。

表1 1#应变计标定数据

图2 各计算式的绝对误差曲线（1#）

从图2中可见利用式（4）、（5）、（6）与式（3）结合计算拟合出来的误差曲线偏离零点较远且离散性大，进一步计算得到最大误差分别为1.34%FS、0.83%FS、0.61%FS。而利用式（7）、（8）、（11）计算拟合出来的误差曲线接近零点值且离散型小、 吻合度较好，其最大误差分别为 0.157%FS、0.161%FS、0.191%FS。很明显，式（7）、（8）、（11）的拟合精度比式（4）、（5）、（6）与式（3）结合计算拟合的精度要高。也说明模型二、三、四比模型一的拟合精度高。为进一步验证模型公式精确性，利用同类型的2#、3#应变计做了重复性试验（见图3、4）。2#应变计利用上式拟合计算出来的最大误差分别为 0.410%FS、0.342%FS、0.285%FS、0.121%FS、0.117%FS、0.128%FS。3#应变计利用上式拟合计算出来的最大误差分别为0.629%FS 、0.362%FS、0.267%FS、0.089 9%FS、0.090 0%FS、0.101 0%FS 。重复性试验结果同样表明式（7）、（8）、（11）三式比式（4）、（5）、（6）分别和式（3）结合拟合计算出来的误差要小、精度要高、曲线的离散性小、与真值曲线的吻合度要好。由此可以得出数学模型二、三、四的拟合精度相当，且误差不超过0.03%FS。模型一的拟合精度最差。

图3 各计算式的绝对误差曲线（2#）

图4 各计算式的绝对误差曲线（3#）

式（4）、（5）、（6）是模型一中系数K值得三种不同的计算方法。从以上实验结果看出利用最小二乘法[即式（6）]拟合的结果与实测结果比较吻合，这也是国标及生产商在出厂标定时一直采用的计算方法。式（5）次之，式（4）最差。尽管模型二的拟合精度高，但是由于该模型中不含初频f0项，初频漂移后该式无法使用,该模型存在一定的缺陷。模型三和模型四的拟合值都与实测结果相吻合，且相互之间的误差微小（仅为0.01%FS），两模型都是很好的拟合计算方法。进一步观察发现两模型中都含有一共同项：fi2- f02，且都含有f0项。两模型的区别在于另外一项不同，进而导致了拟合系数和结果的差异。模型四与模型三的异同点在于模型四的修正项是二次项而模型三是一次项，从计算方法上讲模型三更简单，且能够直接从频率上计算出应变量的差值。笔者认为模型三是以上四个模型中最理想的拟合计算方法。此外，可以发现图1和图2与图3的误差变化趋势是相反的，这可能是由于应变计本身特性的原因所致。

图5、图 6和图 7分别为式（7）、（8）、（11）三式中各项参量对拟合值的贡献量关系。从图5中可以看出式（7）中b fi项与拟合值相近，是主导项，其余为修正项。这与振弦式应变计的原理不符。尽管该式的拟合精度高，但是无法从原理上说明该式的根据，何况该式无初频 f0项，因此不适合做为振弦式应变计的数学模型。在图6和图7中项对拟合值的贡献量最大，是主导项，这符合振弦式应变计的原理，修正项对拟合值的贡献量小，但不可缺少。

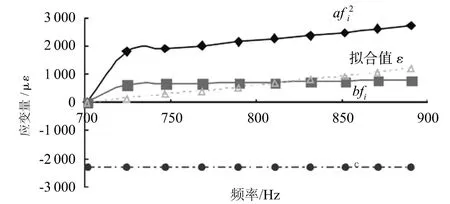
图5 式（7）中各项对拟合值的贡献量

图6 式（8）中各项对拟合值的贡献量

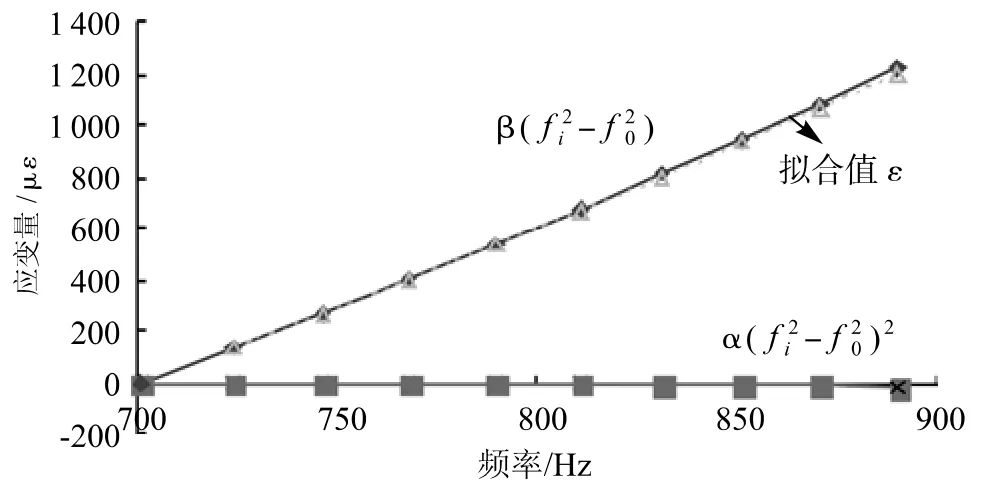
图7 式（11）中各项对拟合值的贡献量

4 结语

从以上几个数学模型比较分析的结果来看，模型一的三种计算方法误差都大，不适合作为高精度振弦式应变传感器的数学模型；模型二中不含初频f0项，初频漂移后该式无法使用,该模型存在一定的缺陷；模型三和模型四的计算拟合精度都高，但是由于模型四是高次多项式，计算相对较复杂。根据振弦式应变计的本质和原理，fi2- f02项是模型中不可或缺的一项。因此综合各因素，模型三形式简单、计算拟合精度高，是四个模型中最好的（这与王学水等人得到的结论是一致的），该模型不仅适用于振弦式压力传感器、位移传感器，而且也适用于振弦式应变传感器，应当加以推广和应用。

[1]B.Benmokrane, M.Chekired,H.Xu, Monitoring behavior of grouted anchors using vibrating-wire gauges[J]. Journal of Geotechnical Engineering-ASCE, 1995(121)： 466-475.

[2]聂洪江, 高春林, 孙纪华. 基于振弦式传感器的大坝安全监测系统的研究[J]. 河南水利与南水北调, 2010(10)： 76-77.

[3]D.Coutts, J.Wang, J.Cai.Monitoring and analysis of results for two strutted deep excavations using vibrating wire strains gauges[J].Tunnelling and Undergroud Space Technology, 2001(16)： 87-92.

[4]宋振骐, 宋振骐. 实用矿山压力控制[M]. 徐州： 中国矿业大学出版社, 1988： 295-296.

[5]杨伟, 高至飞, 杨纯燕. 振弦式应变仪在桥梁快速检测中的应用[J]. 山西交通科技, 2006. 06(3)： 62-64.

[6]吕惠卿, 张湘伟, 张荣辉, 等. 振弦式应变计在水泥混凝土路面力学性能测试中的应用[J]. 公路交通科技, 2006： 61-63.

[7]袁广超, 田旭东, 张恩, 等. 振弦传感器在船舶应力监测系统中的应用[J].技术与应用, 2009(03)： 36-39.

[8]王学水, 邓铁六. 振弦式传感器标定曲线的拟合公式[J]. 传感器技术, 1994(3)： 37-39.

[9]崔玉亮, 刘永明, 于凤. 谐振弦式传感器理论公式修正方法及应用[J]. 测试技术学报, 1996, 10(1)： 19-22.

[10]Feng Yu, Naren Gupta. An efficient model for improving performance of vibrating-wire instruments[J]. Measurement, 2005(37)： 278-283.

[11]白泰礼, 邓铁六, 谢军, 等. 振弦式传感器的精确数学模型及其应用[J]. 岩石力学与工程学报, 2005，11(24)： 5965-5969.

[12]美国基康公司. 振弦式传感器使用说明书.