弹性复合圆柱滚子轴承静态径向刚度分析

姚齐水 张 然 明兴祖 杨 文

湖南工业大学，株洲，412007

0 引言

圆柱滚子轴承因其滚动体与滚道为线接触、径向承载能力和径向刚度较高的特点，广泛应用于各类机械设备中。目前使用的圆柱滚子轴承的滚动体一般为实心圆柱滚动体（或外表面带有一定凸度的实心圆柱滚动体）和空心圆柱滚动体（去掉实心圆柱滚动体中心部分的材料，将滚动体做成空心状）两种。从实际应用中发现，实心圆柱滚子轴承存在传动精度不高、振动噪声大、高速和重载情况下容易损坏等不足，空心圆柱滚子轴承具备较高的传动精度和振动性能等优点，但受载空心滚动体处于周期性的交替变形状态，空心滚动体的内壁容易弯曲疲劳断裂，因此，研制具有高精度、高转速、高寿命的圆柱滚子轴承在工程上具有特别重要的意义。笔者根据组合创新的原理，在保留实心圆柱滚子轴承和空心圆柱滚子轴承优点的基础上，提出了一种全新的弹性复合圆柱滚子轴承，并申请了专利［1］。

轴承的刚度是轴承的重要参数之一，定义为轴承内外套圈产生单位的相对弹性位移量所需要的外加载荷。刚度参数对整个系统的振动、噪声、寿命有着非常重要的影响，研究弹性复合圆柱滚子轴承的刚度十分必要。国内外许多学者对实心圆柱滚子轴承和空心圆柱滚子轴承刚度的研究做了大量工作：Harris等［2］给出了点接触和线接触情况下轴承的接触应力分布和接触变形公式；Erwin等［3］给出了计算线接触圆柱滚子轴承弹性变形的近似公式；陈家庆等［4］利用曲梁理论推导出空心圆柱滚子轴承接触变形公式；刘卫群等［5］利用PSARB程序编写的程序分析了滚动轴承的刚度；李伟健等［6－7］利用当量弹性模量的分析方法推导出了空心圆柱滚子轴承的刚度计算公式。考虑到弹性复合圆柱滚子轴承结构上的特殊性，不能直接应用上述的研究结论。本文将在分析计算弹性复合圆柱滚子轴承载荷分布的基础上，利用有限元仿真的方法计算轴承的受载变形，结合刚度的定义，推导出弹性复合圆柱滚子轴承静态径向刚度的计算公式；再通过弹性复合圆柱滚子轴承刚度的计算，分析填充度、外载荷、滚子数三者对弹性复合圆柱滚子轴承刚度的影响规律，并和空心圆柱滚子轴承的刚度进行比较。

1 载荷分布［8］

弹性复合圆柱滚子轴承结构如图1所示。弹性复合圆柱滚子轴承是在空心圆柱滚子轴承的滚动体中嵌入聚四氟乙烯材料，用以改善滚动体内壁的应力状态，减小内壁弯曲疲劳应力，提高承载性能［9］，延长轴承的安全服役寿命［8］。为了便于分析计算，作如下假设：①轴承内外圈均为刚体，不发生变形；②所有的弹性变形均发生在滚动体上；③轴承外圈静止，内圈在外载荷作用下发生相应的位移；④滚动体和内部的填充物之间粘结良好，可看作一个整体结构。

图1 弹性复合圆柱滚子轴承结构图

轴承在承载过程中受接触变形等原因的影响，不同位置的滚动体所承受的载荷和弹性变形都不同，所以研究在受载情况下的载荷分布具有十分重要的意义。如图2所示，在不考虑径向游隙的情况下，轴承在承受径向载荷Fr时，内圈中心从O点沿径向移动到O′点，相对于外圈产生径向位移δ。假设有一个滚动体的中心位于径向负荷的作用线上，取最下面的滚动体编号为0，产生的弹性变形量为δ0（在径向游隙为0的情况下δ0＝δ），从最下面的滚动体向两边依次给每个滚动体编号，则第i个滚动体上产生的理论变形量为δi。

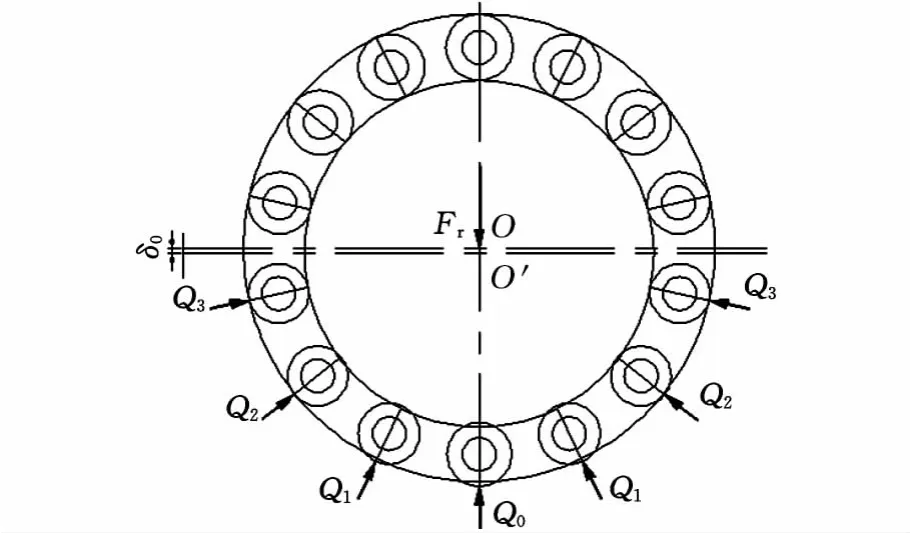
图2 弹性复合圆柱滚子轴承受径向载荷时的载荷分布

式中，φi为第i个滚动体中心和外圈中心连线与径向负荷作用线之间的夹角；N为轴承单边接触滚动体数。

根据轴承整体的受力平衡可得

变形协调方程如下：

式中，Z为滚动体总数；t为指数，线接触时，t＝0.9。

联立式（2）～ 式（5）并且代入式（1）可求得

其中，对于圆柱滚子轴承，有

通过式（6）可求得Q0的一个初始值，再代入式（1）～ 式（5）反复进行迭代运算，求得Q0的一个精确值，最后通过式（3）可求得弹性复合圆柱滚子轴承在承受径向载荷时每个滚动体所承受的载荷。

2 接触变形有限元仿真计算

根据 GB／T4661－2002以及 GB／T283－2007来确定本文所要分析的弹性复合圆柱滚子轴承的各项参数，如表1所示。

表1 弹性复合圆柱滚子轴承参数

应用ABAQUS软件进行有限元建模，根据上述假设①和假设②，不考虑内外圈的接触变形，利用文献［7］中所用方法，将轴承内外圈的弹性模量设置为206TPa（该弹性模量远大于滚动体外圈弹性模量，接触变形可忽略），泊松比为0.3。考虑到轴承受力的对称性和轴承的滚子数，在建立模型时，分别取1／20的轴承内外圈和1／2的滚动体进行分析，在不影响计算结果的前提下，将内圈的内表面和外圈的外表面简化为平面。采用单元类型为三维二次完全积分单元来对模型进行网格划分。由于滚动体与内外圈接触区域的接触半宽很小，容易产生应力集中，将此区域网格进行局部细划，而内外圈基本不发生变形，对计算结果影响不大，此区域网格划分相对较粗。在定义相互作用时，对滚动体外圈和内部填充物施加绑定约束；而滚动体和滚道之间的接触采取面面接触，以内外圈接触面为主面，滚动体接触面为从面，对内外圈与滚动体之间分别设立接触对。有限元分析模型如图3所示。

图3 弹性复合圆柱滚动体与内外圈接触有限元分析模型

边界条件的设置在有限元的分析中起着非常重要的作用。工作过程中轴承外圈与轴承座之间不会发生相对转动，可视为固定，在外圈外表面添加所有自由度的约束；在模型的剖面处施加对称约束；在内圈的端面处施加轴向的约束。在内圈的内表面施加总和为Qi／2的均布载荷，内圈在边界条件和径向载荷的作用下，只能沿着y轴方向移动，而这部分位移则会被滚动体和内外圈的变形所吸收，即内圈在y轴上的位移就是滚动体所产生的径向变形量的大小。

3 刚度计算公式

轴承的径向刚度是指轴承内外套圈产生单位的相对弹性位移量所需的外载荷，轴承的径向刚度等于轴承所受径向载荷除以径向变形，结合载荷分布公式可得

4 计算结果及分析

定义滚动体的填充度为k，k＝d／D，其中d为填充物的直径，D为滚动体外圈的外径。取不同径向载荷和不同填充度的弹性复合圆柱滚子轴承，结合载荷分布公式以及弹性变形的有限元计算结果，对弹性复合圆柱滚子轴承的径向刚度计算结果如表2所示。

表2 不同填充度、不同载荷情况下弹性复合圆柱滚子轴承的刚度值 MN／m

4.1 填充度对刚度的影响

填充度是影响弹性复合圆柱滚子轴承刚度的一个非常重要的因素，填充度过小则对轴承的接触状态和变形影响不大［10］，无法体现弹性复合圆柱滚子轴承的优势，填充度过大则容易变形过大而产生破坏，本文取填充度从40%到70%的情况来分析。为分析方便，将表2的数据进行处理，结果如图4和图5所示。可以看出：在相同载荷情况下，随着滚动体填充度增大，弹性复合圆柱滚子轴承的刚度都是迅速减小的；填充度在40%到55%之间，随着外载荷增大，轴承的刚度都有着明显的增大趋势；填充度在60%到70%之间，随着载荷增大，轴承的刚度基本上变化不大，在70%时，刚度甚至趋近于一条水平线。

4.2 径向载荷对刚度的影响

径向载荷是另一个对轴承刚度影响很大的参素，从图4和图5中可以看出，径向载荷对轴承刚度的影响是随着填充度的不同而不同的。外载荷在30kN到100kN之间时，随着填充度增大，轴承的刚度迅速减小；而当径向载荷等于10kN时，随着填充度增大，轴承的刚度减小趋势明显变小。径向载荷越小，随着载荷增大，对轴承的刚度提升就越大；径向载荷越大，随着载荷增大，对轴承的刚度提升幅度就越小。

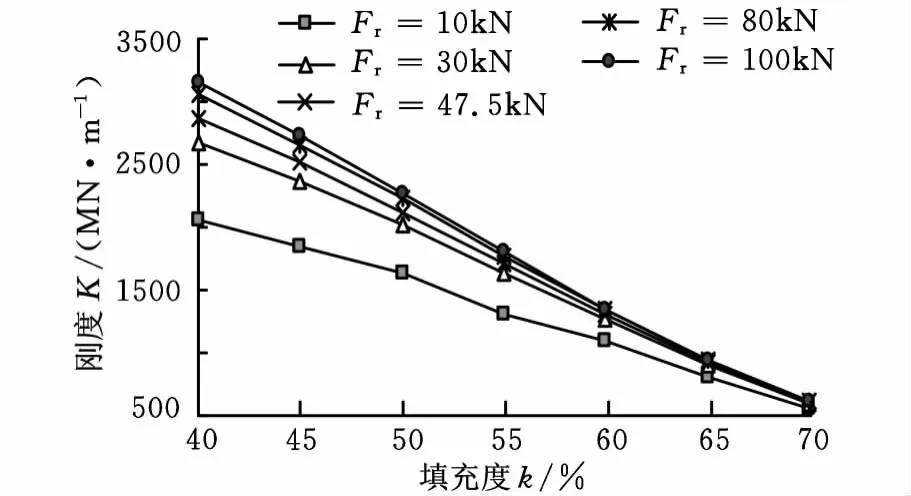
图4 轴承刚度与填充度的关系图

图5 轴承刚度与径向载荷的关系图

4.3 滚子数对刚度的影响

由式（1）～式（6）可知，滚子数对轴承的载荷分布有着非常重要的影响，进而也影响着轴承的刚度值。表3表明，在相同外载荷和填充度的情况下，随着滚子数增多，弹性复合圆柱滚子轴承的静态径向刚度逐渐增大；填充度越小，滚子数的增加对轴承的刚度提升幅度越大，填充度越大，滚子数的增加对轴承的刚度提升幅度越小。滚子数越多，随着填充度增大，轴承的刚度减小越明显。

表3 Fr＝47.5kN时，不同滚子数、不同填充度情况下弹性复合圆柱滚子轴承的刚度值 MN／m

4.4 和空心圆柱滚子轴承刚度比较

从表4不难发现，相同填充度和空心度（即针对空心圆柱滚子轴承的参数）的弹性复合圆柱滚子轴承的刚度一直比空心圆柱滚子轴承大，填充度（空心度）越大，弹性复合圆柱滚子轴承和空心圆柱滚子轴承的刚度差越大。填充度为40%的弹性复合圆柱滚子轴承和空心度为40%的空心圆柱滚子轴承的刚度差小于1%，几乎可以忽略；而填充度为70%的弹性复合圆柱滚子轴承和空心度为70%的空心圆柱滚子轴承的刚度差约为4%，已经不能够完全忽略。这是由于在填充度较小的时候，填充度所占的体积比较小，对轴承的刚度影响不大，随着填充度增大，填充物所占的体积比越来越大，所承受的力越来越大，对轴承的影响也就越来越大。

表4 Fr＝47.5kN时，弹性复合圆柱滚子轴承和空心圆柱滚子轴承的刚度值比较 MN／m

5 验证

弹性复合圆柱滚子轴承与实心圆柱滚子轴承仅在滚子内部结构方面存在差异，两者与内圈形成的接触副的情况相似，可以将分析实心滚子轴承时建立的有限元模型用来分析弹性复合圆柱滚子轴承的接触问题［11］。反之，用与上述弹性复合圆柱滚子轴承有限元分析模型相似的方法对实心圆柱滚子轴承的接触变形进行有限元分析；分析过程中设定相同的边界条件，模型中的内外圈材料和弹性复合圆柱滚子轴承分析时相同，实心滚动体的材料和弹性复合圆柱滚子轴承的滚动体外圈相同。有限元分析模型如图6所示。

图6 实心圆柱滚动体与内外圈接触有限元分析模型

通过有限元计算得到了实心圆柱滚子轴承的受载变形的关系，并和帕姆格林经验公式［3］所求得的结果进行比较，所得结果如图7所示。

由图7可见，本文所用的有限元计算模型在计算实心圆柱滚子轴承接触变形时所得结果与帕姆格林理论公式所求的结果基本接近，充分说明了本文所用的有限元计算模型用于计算轴承滚动体的接触变形是比较可靠的，求解的精度也能符合计算的标准。

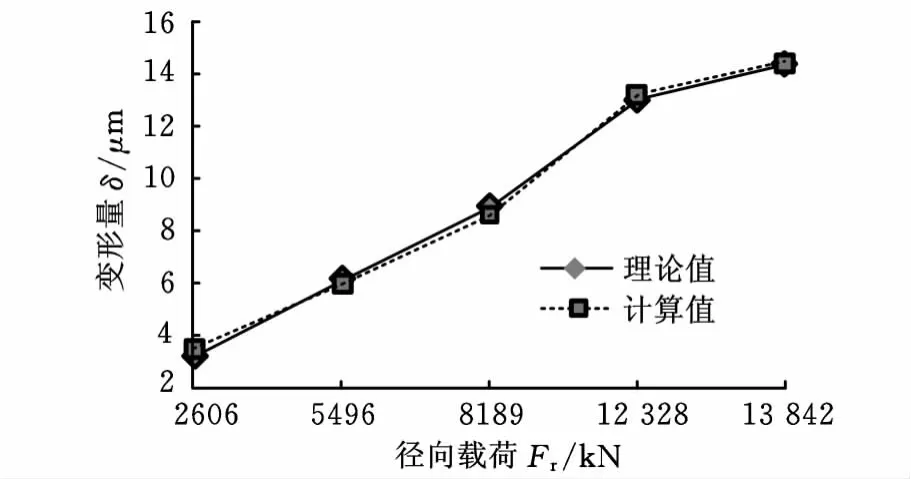
图7 轴承实心圆柱滚子轴承接触变形有限元计算值与理论值比较

6 结论

（1）填充度在40%到55%之间，随着外载荷增大，轴承的刚度有着明显的增大趋势；填充度在60%到70%之间，随着载荷增大，轴承的刚度基本上变化不大，填充度为70%时，轴承的刚度甚至趋近于一条水平线。

（2）外载荷较大，随着填充度增大，轴承的刚度迅速减小；而当外载荷较小时，随着填充度增大，轴承的刚度减小趋势明显变小。外载荷越小，随着载荷增大，对轴承的刚度提升就越大；外载荷越大，随着载荷增大，对轴承的刚度提升就越小。

（3）填充度较小的情况下，滚子数的增加对轴承的刚度提升幅度比较大；填充度较大的情况下，滚子数的增加对轴承的刚度提升幅度比较小。

（4）相同填充度和空心度的弹性复合圆柱滚子轴承的刚度一直比空心圆柱滚子轴承大，填充度（空心度）越大，弹性复合圆柱滚子轴承和空心圆柱滚子轴承的刚度差越大。

［1］姚齐水.一种弹性复合圆柱滚子轴承：中国，201120066406.1［P］.2011－11－23.

［2］Harris T A，Kotzalas M N.Advanced Concepts of Bearing Technonlogy［M］.New York：Taylor ＆Francis，2006.

［3］Erwin V，Zaretsky A.Palmgren Revisited－abasis for Bearing Life Prediction［J］.Journal of the Society of the Tnbologists and Lubrication Engineers，1998，54（2）：18－23.

［4］陈家庆，毛红兵，张宝生.无预载荷空心圆柱滚子轴承的理论研究［J］.轴承，2002（6）：1－5.Chen Jiaqing，Mao Hongbing，Zhang Baosheng.Theoretical Research on Hollow Cylindrical Roller Bearing Without Preloading［J］.Bearing，2002（6）：1－5.

［5］刘卫群，罗继伟，吴长春，等.滚动轴承刚度分析程序［J］.计算力学学报，2001，18（3）：375－378.Liu Weiqun，Luo Jiwei，Wu Changchun，et al.Program for the Stiffness Analysis of Rolling Bearing［J］.Chinese Journal of Computational Mechanics，2001，18（3）：375－378.

［6］李伟建，潘存云，王荣吉.空心圆柱滚子轴承刚度分析［J］.中国机械工程，2009，20（7）：795－798.Li Weijian，Pan Cunyun，Wang Rongji.Stiffness Analysis of Hollow Cylindrical Roller Bearings［J］.China Mechanical Engineering，2009，20（7）：795－798.

［7］李伟建，潘存云，王荣吉，等.空心圆柱滚子接触变形的一种计算方法［J］.轴承，2009（8）：1－5.Li Weijian，Pan Cunyun，Wang Rongji，et al.An Analytical Method for Calculating of Hollow Cylindrical Roller Contact Deformation［J］.Bearing，2009（8）：1－5.

［8］姚齐水，杨文，余江鸿，等.弹性复合圆柱滚子轴承结构设计研究［J］.中国机械工程，2012，23（1）：2899－2902.Yao Qishui，Yang Wen，Yu Jianghong，et.Research on Structure Design of Elastic Composite Cylindrical Roller Bearing［J］.China Mechanical Engineering，2012，23（1）：2899－2902.

［9］杨文，姚齐水，余江鸿，等.弹性复合圆柱滚子轴承承载性能的理论研究［J］.机械传动，2013，37（5）：6－9.Yang Wen，Yao Qishui，Yu Jianghong，et al.Research of Carring of Elastic Composite Cylindrical Roller Bearing［J］.Mechanical Transmission，2013，37（5）：6－9.

［10］魏延刚.空心圆柱滚子与滚道接触应力及位移分析［J］.轴承，2003，5（5）：1－5.Wei Yangang.Study on Capacity Performance of Hollow Cylindrical Roller Bearing without Preloads［J］.Bearing，2003，5（5）：1－5.

［11］李伟健，潘存云，王荣吉.3种滚子接触的有限元分析［J］.中国铁道科学，2009，30（3）：109－112.Li Weijian，Pan Cunyun，Wang Rongji.Finite Element Analysis of Three Types of Roller Contact［J］.China Railway Science，2009，30（3）：109－112.