林木风倒动态模型的建立与分析

贾 杰，李静辉

（东北林业大学土木工程学院，哈尔滨 150040）

风倒是森林中最常见的自然灾害，也是形成林隙的主要原因。风倒现象主要是指林木在风荷载作用下发生倾倒，甚至连根拔起的现象。其破坏方式包括了干折、根折和连根拔起等三种。其成为森林生态的一个扰动因子。根据数据统计显示，全世界每年非灾害性风倒造成的木材减产在15%以上［1］。风力对林木的结构、组成、树冠结构、物种组成及植物生长等都有很大的影响。近年来，随着全球气候环境的急剧变化，风倒导致森林破坏的情况频繁发生。因此，展开对风倒机理的相关研究日益受到科学研究人员的重视，搞清风倒的机理对于木材生产实践和生态学的理论研究都有极其重要的意义。

目前，国内很多学者在林木风倒机理方面进行了深入的研究，李国旗等［2］利用现有理论研究了位于不同风压和高度处树木的应力分布规律。陈少雄［3］、陈士银［5］等学者基于野外调查和统计的方法分别研究了泡桐、桉树和木麻黄等树种的抗风性与个体特征之间的关系。代力民等［6］从生态学角度出发研究林隙的形成原因。上述研究涉及风倒的力学理论模型的较少，只有哈尔滨工业大学的张少实课题组［7］做过一些研究，分别从静力学和动力学角度建立了风倒的模型，并展开了相应的分析，但是这种动力学模型是基于云杉单个物种且简化成一端固定，一端连接质量团的弹性杆，这种模型单一且局限性很大。在国外，例如英国、加拿大、美国等一些欧美国家学者，对张子松、西特云杉等树种的风倒机理进行了深入的、广泛的研究［9］。通过动力学理论推导，结合野外试验中林木和土壤力学参数的测定，地形数字高层模型和实物模型风洞试验，获得了复杂地形下和不同林分密度时的风场分布，建立了一系列力学方程来描述林木的抗风性［10］，对风倒的力学机理也进行了相应的阐述，形成若干关于林木风倒机理的模型。如MC2［11］、HWIND［12］等，尽管这些研究代表了风倒机理研究的国际先进水平，但主要是基于材料力学方法的线性力学模型［13］。虽然正确的描述了风倒机理的许多方面，但受研究条件等的限制在系统设计时对关键环节进行了简化，造成模型与实际情况之间的误差。所以如何正确建立风倒的力学模型，和建立模型时对实际情况进行怎样的简化或近似，而使模型与实际情况达到最大的吻合，成为了风倒现象研究的最主要问题。

本文在考虑林木外部形态的前提下给出假设条件，将林木看成由一根无质量弹性杆连结，并建立了林木的动态力学模型，列写出模型的振动方程，边界条件和初始条件，同时将平均和动态的风速、平均和动态的位移、以及茎部的力与力矩都联系在一起，假设这些力和力矩是折断现象的标准值。充分考虑风、树和根系三者的关系，推导出无阻尼和有阻尼情况下林木风倒的动态模型，为后续林木风倒的频率域、时域分析奠定理论基础，同时也为风荷载作用下系统的受迫振动以及风倒的条件分析提供理论模型。

1 模型建立

基本的力学模型如图1所示，两部分集中质量，一部分代表树冠（对树木而言）的集中质量，一部分代表根系的集中质量。这两部分质量由一根无质量弹性杆连结，其长度等价于从地面到树冠的重心。模型系统各个要素部分的受力介绍如下:①将在茎秆顶部作用的振动风载荷定义为P。②树冠的等价质量定义为m。（之所以是等价，是因为可以适当的考虑茎秆的质量，给出适当的允许系数，将茎秆的质量加在上部集中载荷处）③树冠的惯性质量定义为是上部集中质量的瞬时位移。④在树干高度为处的位移为y，根据经典的欧拉公式，可以知道在x处的力矩为是茎秆的弹性模量，I是茎秆的在处的惯性矩，定义EI为抗弯刚度。⑤将根系对于旋转的阻力矩定义为是单位角度阻力矩系数，可以看出集中质量的旋转惯性力定义为0，H为下部集中质量的惯性矩系数。

基于前期文献的参考，本文采用的模型是合理的，也是实际的。由于树木在倾斜的过程中根部的集中质量是变化的，所以必须考虑到根部的旋转惯性力也是变化的，如果这点做不到的话，那么根系处的土壤对模型的作用力只能作用在茎秆处，考虑到根系及土壤的变化和风倒现象联系紧密，条件⑥是必需的。而模型系统的阻尼主要来自于三个方面:在茎秆和根系处的能量消耗，空气对于树木运动的阻力，树木相互之间的影响。而分析时先考虑无阻尼情况。一个优化的、简易的、可变性很强的模型是很容易将无阻尼推广到阻尼情况下。

先考虑图1上半部分的平衡关系，可以得到:整体阻力矩和根部所倾斜的角度成比例。⑥将下部

图1 力学模型图Fig.1 The mechanical model

如果假设风力用正弦函数的形式给出Pejωt，而P是振动的最大值，j是－1的平方根，ω是角频率（等于2πn，n是自然频率），t表示时间，同理将y可以写成yejωt，而Y可以写成yejωt，现在可以将等式变成:

上面的等式可以根据如下三个边界条件来求解:

①当x=0时，y=0。

②当x=X时，y=Y。

③当x=0时，

这个等式即风力对根部所产生的力矩和根系的阻力矩加上下部集中质量的惯量相平衡，也可以写成:当x=0时，如果将树干底部所产生的弯矩用Bejωt的形式给出，那么对于公式 （2），根据三个边界条件，用代数方法便可以求解，得到如下公式:

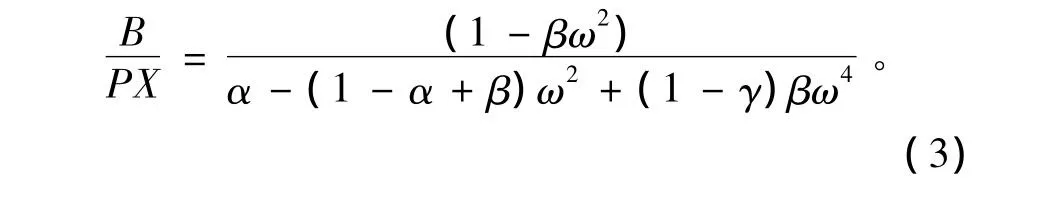
在上式中，ω是一个无量纲的角频率，ω=ωn（X/g）0.5且:

公式描述了树干底部弯矩波动和风力波动之间的关系，从公式中可以看出B/PX随着ω以及三个参数α、β、γ的变化而变化。

在较低频率下，即相应于系统平均值的情况，当ω趋于0的时候，可以得到:

因此只有α对系统具有重要的作用。从公式（4）可以看出，α是一个关于系统参数很复杂的函数。但是，如果适当选取系统参数的时候（较大的树冠质量m，较小的阻力矩系数k），这时B/PX趋于无穷。这刚刚符合静态不稳定现象——树冠太重，以至于根系不能承担其重量。在现实中有一类现象和这个非常吻合，在经过长时期的降雨后，林木树冠重量增加，但是其根系的支持力却在下降，只要在微风情况下就会会发生倾覆现象。

对于系统的自然频率，当β很小，令公式（3）中分母为0（即B/PX趋于无穷），这是可以得到两个解，（αg/（1－α）X0.5/2π和（（1－α）g/（1－γ）βX）0.5/2π，两者即为系统的自然频率。

基于其他学者前期的研究工作，本文给出典型的稻类、有叶悬铃树、无叶悬铃树和西特云杉等四类林木的模型参数值，见表1。

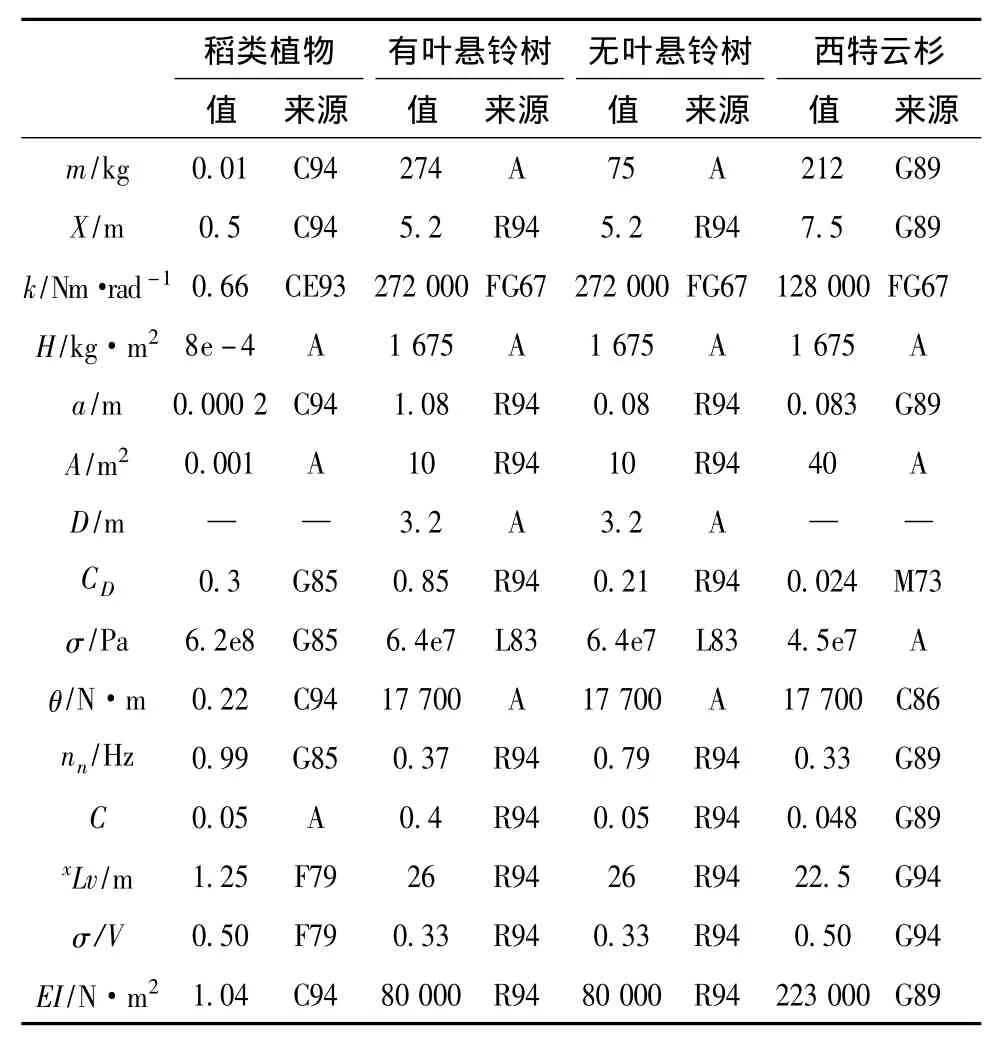
表1 模型参数值Tab.1 Values of parameters in the model

表2 参数α、β、γ及导出的自然频率Tab.2 Derived parametersα、β、γ and calculated natural frequencies

表2给出了α、β、γ的详细数值，以及根据以上关系所导出的自然频率。很明显，这三个参数都是无量纲量，可以适用于任何情况，具有普遍意义。而根据理论计算所得到的较低频率值和表1中所获得的测量值有很好的吻合，尽管在表1中对个别参数进行了大胆的假设。但在计算悬铃树质量的时候，并不是根据实际测量得到，而是根据在位移已知的情况下，反向计算树冠集中质量，所以从某种意义上说，所预想的频率值并不完全独立。

图2描述了四种不同林木B/PX和频率n的关系，（a）是稻类植物的曲线图，（b）和 （c）是悬铃树在有叶和无叶情况下的曲线图，（d）是西特云杉的曲线图。四个曲线图有一些共同的特点，在较低频率时，比率是连续的，但当第一个自然频率邻近的时候，所有图的比率都趋于无限。在自然频率处，比率发生突变，产生了一个不连续的现象，在频率稍高于自然频率的时候，所有图示中比率都几乎降为0，当频率逐渐增加到接近较高自然频率的时候，比率急剧上升且发生突变，这和第一个自然频率处的现象比较相似。这些高频率峰是较低频率值的2～3倍。高频率峰的出现可能是由于在森林中采取不恰当的频率谱所造成的。最新的研究表明，树的波动事实上不是随机的，而是在自然中有间断的波动。也就说这些频率峰并不是前面所提到的较高频率，而是在较低频率下的谐振动给人们造成的假象。鉴于没有明显的数据表明较高频率可以在实践中得到检验，可以对模型进行简化。

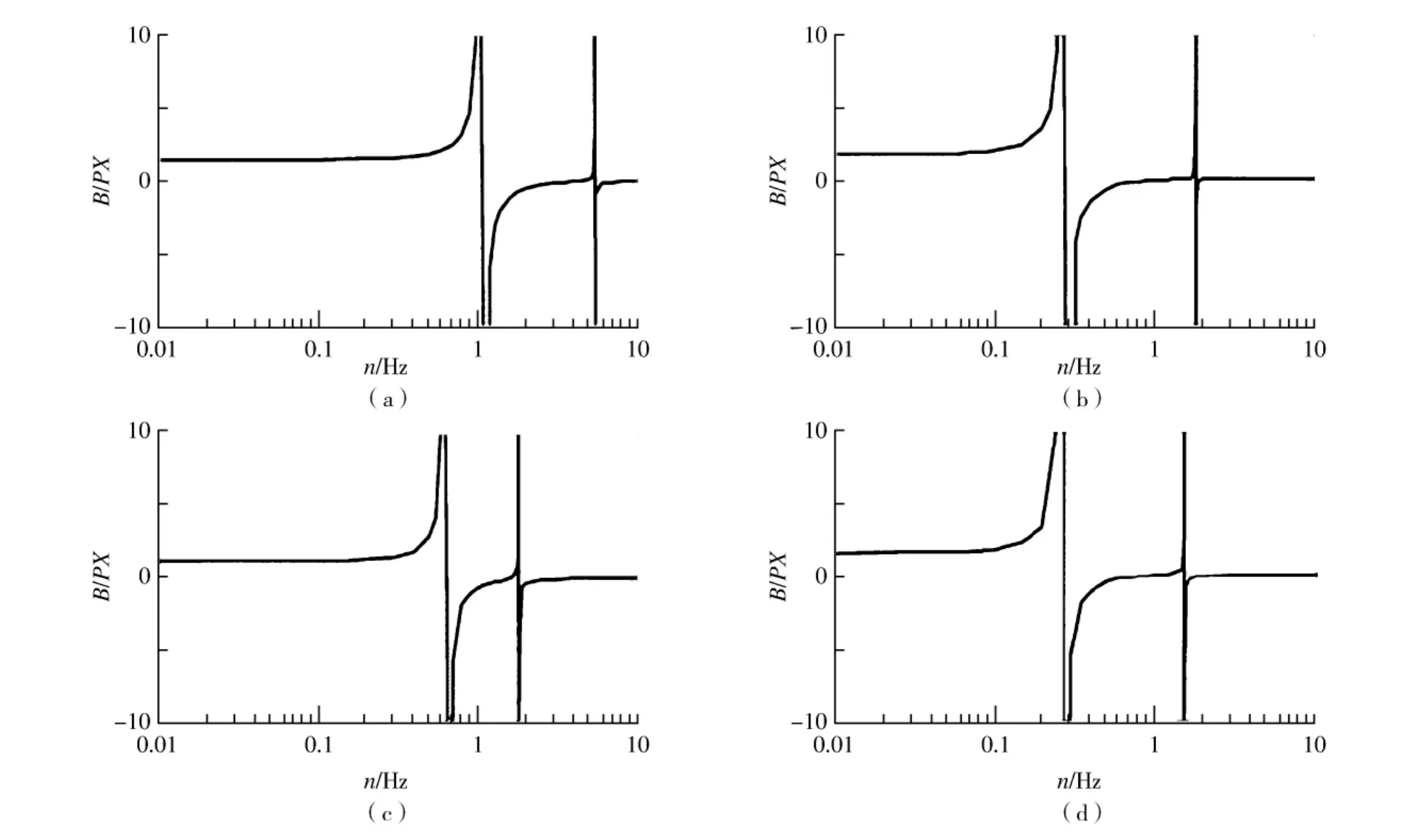
图2 不同树木和频率的关系曲线图Fig.2 Different trees and freguency relationship

2 模型的简化

从表2中β值可以看出，β一般都比较小，可以β让取0值，这是一个合理的假设，那么公式（3）可以变成:

公式中的无量纲角频率

在公式 （3）中，没有模拟较高的自然频率，但在计算β值的时候，公式 （3）和公式 （9）并没有太大的区别。根据公式 （8），可以重建简化后系统的动态模型，在无阻尼情况下:

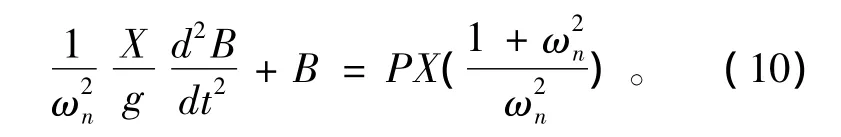
基于简化后的模型，系统可以模拟有阻尼情况下的运动形式，如下。

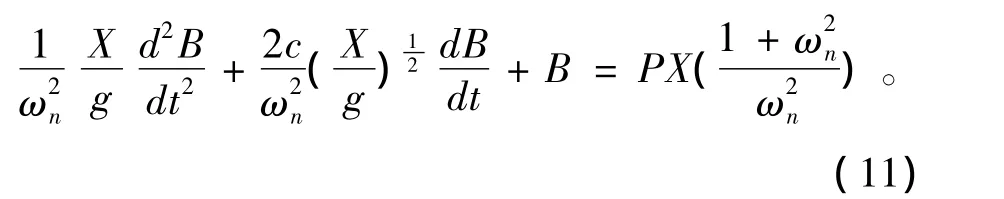
c表示有阻尼情况下的阻尼率。公式 （11）是有阻尼谐振动下的标准公式，B/PX与无量纲角频率ωn的关系是:

公式 （11）和 （12）从本质上揭示了系统的控制参数是无量纲的角频率，从公式 （4）和公式（9）又可以看出，角频率只是一个和系统本身参数以及阻尼率有关的量。当ωn取1.8，就可以得到B/PX在不同阻尼率情况下的与频率ω的关系，如图3所示。

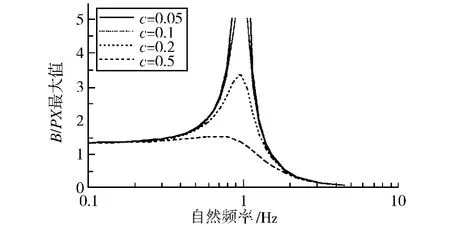
图3 在阻尼谐振动下的转移函数Fig.3 Transfer function for damped harmonic oscillator

由公式 （12）可以看出，无量纲的自然角频率对估计林木的稳定性是一个极其有用的参数，和稳定性有着直接的关系。比率B/PX实际上是相对于静态风载作用于上部集中质量所产生的力矩的放大率，在没有阻尼情况下，将趋于无穷。基于能量法，得到树木的自然频率，其表达式为

式中:nn表示有量纲的自然频率，λ是常数，a表示茎秆底部的半径，ρw表示树木的密度。对于刚度比较大的树干，即k和EI都比较大的时候，式（4）和 （9）给出了nn的计算方法:

公式 （13）和 （14）看起来很近似，其中ρwπa2和m/X都表示在长度方向的质量集度。但公式 （13）的优点在于考虑了根和土壤的影响，因为不同土壤潮湿程度对自然频率都会有影响。

关于阻尼率，阻尼率是由于树木或者植被的相互影响，空气动力的阻尼以及树木本身的阻尼所产生。以西特云杉为例，Milne指出这三者之间的比例关系是5∶4∶1［14］。从上面的分析可以看出，阻尼率是关于风速的一个常数。但是必须指出，在空气动力阻尼和风速成比例的情况中，这个假设和已有关于空气动力导纳系数的假设以及力和风速关系的结果有些矛盾。但是看到只是林木在柔度比较大的时候，由于其几何变形大，以至于不能得出阻尼和风速的直接关系。

实际上，已有的研究已经测得树木在风载阻力作用下的运动，位移就成为目前研究的一个基本参数［15］。为了将力学模型跟观测相比较，就必须得到位移Y的表达式，从初始的公式 （1）以及公式（11）和 （12），可以得到:

所以，我们可以直接从B得到位移Y。

3 结论

本文展开对林木风倒机理的初步研究，基于林木外部特性，给出了一些理想假设，由此获得了林木风倒的动力学模型，结合外部边界条件和初始条件，同时考虑平均和动态的风速、平均和动态的位移、以及茎部的力与力矩之间的关系，给出树干底部弯矩和风力关系的物理意义，推导出无阻尼和有阻尼情况下林木风倒的动态模型，并给出位移的计算表达式。数值计算结果与实测数据的对比显示出模型的合理性，为后续的研究提供理论基础。林木风倒机理是一个复杂的动态过程，基于理论模型还需要展开进一步相关的研究，首先，由于树木的结构复杂，其内部结构和树冠会对模型产生一些影响，因此需要对模型本身进行一些优化和改进，让模型能够承受更大的位移和累进的根系变化。其次，基于所获得的模型，需要在频率域和时域分别就风速谱、风力谱、弯矩谱以及最大值弯矩谱进行全面的分析。

】

［1］于振良，赵士洞.林隙（Gap）模型研究进展［J］.生态学杂志，1996，16（2）:42 －46.

［2］李国旗，安树青，张纪林，等.海岸带防护林4种树木的风压应力分析［J］.南京林业大学学报，1999，23（3）:76 －80.

［3］陈少雄，王观明，罗建中.桉树幼苗不同株行距配置抗台风效果的研究［J］.林业科学研究，1995，8（5）:582 －585.

［4］陈少雄，杨民胜，王理平.尾叶桉造林密度与蓄积量、抗风和材性关系研究［J］.林业科学研究，1998，11（4）:435 －438.

［5］陈士银.木麻黄不同株行距配置抗台风效果［J］.广东林业科技，1997，13（2）:44 －46.

［6］代力民，徐振邦，杨 丽.红松阔叶林倒木贮量动态的研究［J］.应用生态学报，1999（10）:513－517.

［7］宋晓鹤.云杉风倒静力学模型的建立及其分析［D］.哈尔滨:哈尔滨工业大学，2006.

［8］王 琳.云杉风倒动力学模型的建立与分析［D］.哈尔滨:哈尔滨工业大学，2006.

［9］赖秋明.云杉风倒动力学问题的研究［D］.哈尔滨:哈尔滨工业大学，2008.

［10］Ruel J C，Pin D，Space L，et al.The estimation of wind exposure for windthrow hazard rating:comparison between Strong blow，MC2，topex and a wind tunnel study［J］.Forestry，1997，70（3）:254-266.

［11］England A H，Baker D J，Saunderson S T.A dynamic analysis of windthrow of trees［J］.Forestry，2001，73（3）:225-237.

［12］Benoit R，Desgagne M，Pellerin P，et al.The Canadian MC2:a semi-lagrangian，semi-implicit wideband atmospheric model suited for fine-scale process studies and simulation［J］.Monthly Weather Review，1997，125:2382-2415.

［13］Achim A，Ruel J C，Gardiner B A，et al.Modeling the vulnerability of balsam fir forests to wind damage［J］.Forest Ecology and Management，2005，204:35-50.

［14］Milne R.Dynamics of swaying picea sitchenis［J］.Tree Physiology，1991，9:383-399.

［15］陈俊松，赵 尘，石 迪.森林采运系统动力学模型研究［J］.森林工程，2011，27（1）:78 －81.