带调谐液体阻尼器结构的有限元模拟分析①

吕 晖，张炜超，张向红，吕林涛，温增平

（1．重庆大学土木工程学院，重庆 400031；2．中国地震局兰州地震研究所，甘肃 兰州 730000；3．西安理工大学计算机学院，陕西 西安 710048；4．中国地震局地球物理研究所，北京 1000081）

0 引言

随着建筑业的发展，土木工程结构向着高耸、轻质、大体、和高强方向发展，致使结构的刚度和阻尼不断降低，从而按照传统的抗震设计方法很难满足强震下的舒适度和安全性要求。为了克服传统抗震设计方法的不足，所以研究者们提出了结构控制这一新的方法。调谐液体阻尼器（TLD）就是其中一种有效的结构控制方法。

到目前为止，大多数对TLD的研究都集中在如何利用TLD减小风荷载对结构的作用上面，可以说在这方面确实也取得了巨大的进步。然而由于地震的不确定性，并且就荷载本身而言，地震就比风荷载要复杂，再加上地震中结构的强非线性行为，所以相比对风振的控制，研究TLD对结构地震反应控制就显得要困难得多，正是以上的原因，导致TLD减震方面的相关研究还很不完善，关于TLD减震规律的研究仍是这一技术应用的一项很必要的基础性工作。本文采用有限元分析的方法，将TLD体系简化为平面模型，通过对有限元模型的减震效应分析，研究了TLD的减震规律。

1 TLD的减振机理

TLD－结构体系在受到地震或风荷载作用下发生振动，将带动水箱一起运动，而水箱的运动又会使箱中的液体产生晃动，并引起表面的波浪，这种液体晃动和波浪对箱壁的动压力差，以及液体随结构一起运动引起的惯性力，就构成了建筑物的减振力。单自由度结构－TLD体系，其运动方程可以写为

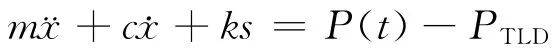
式中m、c和k分别是结构的质量、阻尼和刚度系数；P（t）是作用于结构的动力荷载；PTLD是TLD中液体晃动和波浪所产生的控制力。通过适当调整水箱中液体和波浪的晃动频率，即调整控制力PTLD的作用周期和大小，就可使TLD的控制效果最佳。

2 流固耦合有限元分析方法的原理

在流固耦合分析中，流体压力作用到结构上，同时结构变形引起流体域发生改变。对于大多数耦合问题，ADINA将计算域分为流体域和固体域，流体模型和固体模型通过定义材料属性和边界条件等模型参数在各自计算域中得以确定。

2．1 运动与动力条件

一般来说耦合总是沿着两计算域边界发生。在ADINA中，应用到流固耦合边界上的基本条件是运动条件（位移协调条件）和动力条件（应力平衡条件）：

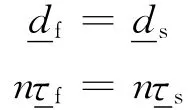
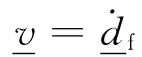
另一方面，根据动力条件，流体的压应力可沿着耦合边界积分得到流体压力，再作用到结构的耦合节点上去。其积分方程如下：

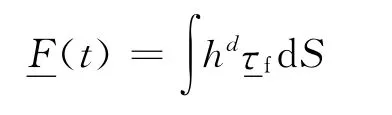
其中hd为结构的虚位移。

2．2 流体和结构的独立网格划分

流体模型和结构模型分别采用不同的单元和网格划分，两种模型的有效性独立限制各自单元的选取。因此在耦合边界两种模型不可能共用节点，具体见图1。

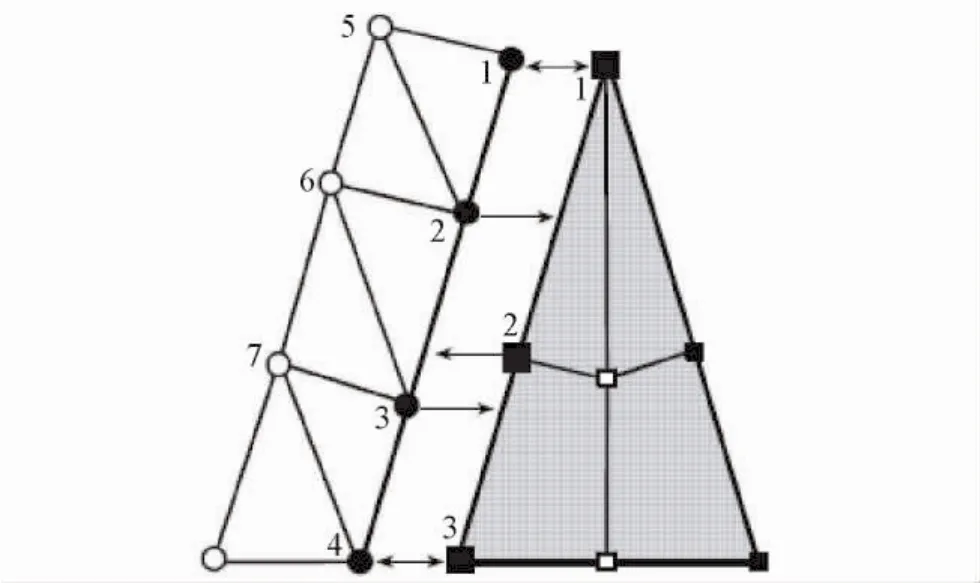
图1 流体和结构的耦合节点Fig．1 Coupling of fluid and solid nodes

由于在流体域和固体域内采用了不同的网格划分，所以在边界上的两种网格存在着不相容的问题，于是在两个模型中相同的几何体也存在着不同的离散表示法。然而两种离散化边界之间的距离必须在一个很小的距离以内，因此ADINA在边界之间定义了两个相对位移：

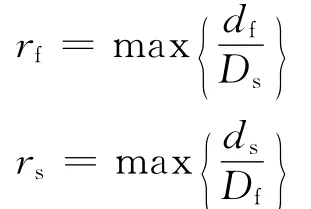
在这里，df是流体节点到结构离散化边界的距离；ds是结构节点到流体边界的距离；Ds和Df分别是结构边界的长度，分别被限制在0．001到1之间（图2）。

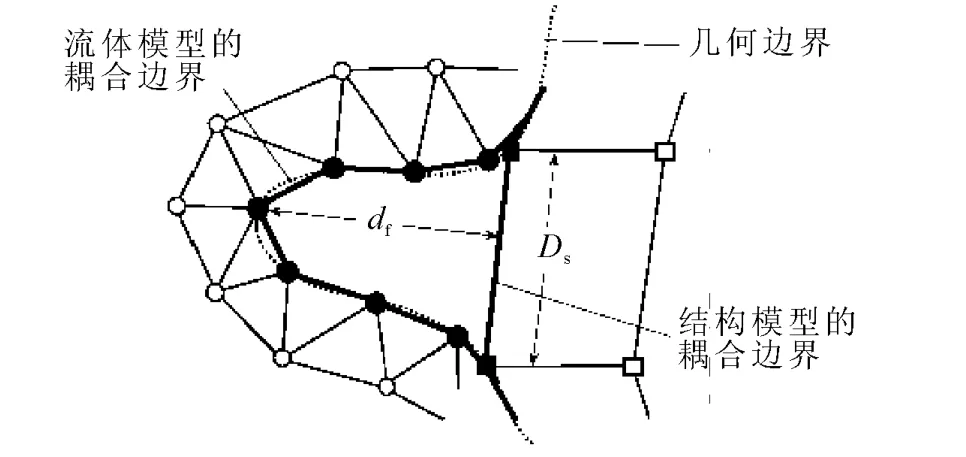
图2 流体与结构耦合边界的距离Fig．2 Measure of the distance between fluid and solid FSI boundaries

2．3 一致时间积分

在流固耦合分析中流体方程与结构方程的时间积分必须保持一致。尽管流体与结构模型中采用了不同的坐标系，但是在流固耦合边界上却采用了相同的坐标系，即拉各朗日坐标系，因此时间积分首先发生在耦合边界，然后再把所得的积分结果应用到整个计算域内。

2．4 耦合系统的有限单元方程

令耦合系统的求解向量为X＝ （Xf，Xs），其中Xf和s分别为定义在流体和结构节点上的流体和结构求解向量。因此，ds＝ds（Xs）和τs＝τs（Xs）。流固耦合系统的有限单元方程可表示为

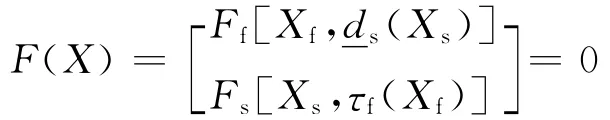
2．5 耦合系统的求解

2．5．1 耦合系统的迭代收敛标准

对于大多数耦合问题，流体的压力将会引起结构的变形，同时结构的位移也会改变流体的形状，这也是为什么要进行流固耦合分析的原因。

尽管结构可以是线性的，但是由于流体方程是非线性，所以耦合方程一定是非线性的，因此，必须用迭代程序求解方程，换句话说，在流固耦合问题中，我们将会得到迭代解：X1，X2，…。在 ADINA中，定义应力和位移作为迭代的收敛标准，其中应力标准和位移标准如下：

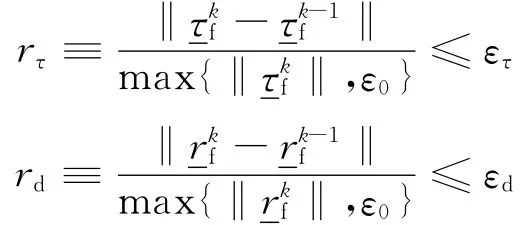
εr和εd分别为位移收敛和应力收敛的容差；ε0为预设常数，其目的是控制位移和应力不致太小，否则将无法控制收敛。

2．5．2 迭代法

这种计算方法也称之为分块法，在这种求解计算中流体和结构的求解变量可以得到充分的耦合。流体方程和结构方程的计算是交替进行的，并且在求解过程中，两方程的迭代解也在不停的进行交换，只有当耦合方程的求解达到收敛，迭代才算完成。在这种方法的求解过程中ADINA引用了一个控制参数：松弛因子，这个因子对求解许多复杂问题都很有用。由于流体和固体模型的求解是在不同的矩阵下进行的，所以这个因子的使用有助于迭代计算的收敛。对于这个求解方法，时间步长和求解域都是由流体模型控制的，而在结构模型中定义的所有时间函数必须要覆盖整个计算域。控制耦合系统收敛的参数也是在流体模型中定义的，其中这些参数是位移容差、应力容差、松弛因子、收敛标准等。相对于直接法，迭代法要求的内存更少，因此，它更适合于稳态分析。

2．5．3 直接法

这种方法也称为同时求解法。和迭代法一样，在直接法中的流体和结构变量也可以得到充分耦合。流体方程和结构方程在同一个坐标系下组合和求解，因此它们在一个矩阵系统下线性化。这个矩阵系统可写为

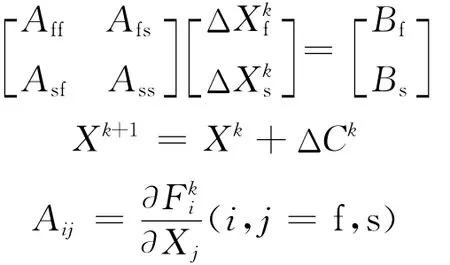
与迭代法一样，流体应力和结构位移也可通过应力松弛因子和位移松弛因子得到松弛。对于直接法来说，所有控制参数的设定基本上与迭代法相同，但是直接法的求解速度要比迭代法快，而且非常试用于瞬态分析。

3 带调谐液体阻尼器结构的有限元建模分析

3．1 有限元模型的建立

建模对象为一个带屋顶水箱的20层平面框架，其中水箱就起到调谐液体阻尼器的作用。在ADNIA中，处理流固耦合问题必须分别建立流体模型和结构模型，所以在建立有限元模型时此20层模型被分解为如图3和4所示的结构有限元模型和流体有限元模型。由于考查的是受调谐液体阻尼器影响下结构整体的动力响应，所以结构可采用由梁单元组成的杆系模型，这样不仅符合实际，而且还节约了求解时间。流体模型则采用ADINA－F提供二维平面流体单元，流体材料属性选为不可压缩层流。在建模过程中特别要值得注意的是：ADINA规定二维流体单元必须建立在YOZ平面，所以为保证与流体模型的一致性，结构模型也必须建立在YOZ平面。

图3 结构有限元模型Fig．3 FE Structure model

图4 流体有限元模型Fig．4 FE Fluid model

在建立流体模型时，边界条件的设置显得尤为重要，为此ADINA－F提供了包括流固耦合边界在内的十四种特殊边界，对于本模型来说，考虑到流体要随结构发生晃动，所以把流体的上表面选为自由表面，而其余的与结构接触的表面都设为流固耦合表面。

在瞬态分析中，为了考察TLD对结构的减振特性及其流场的变化特性，特选用天津波、El Centro波和Taft波作为此流固耦合模型的动力荷载的输入。另外在瞬态求解过程中，对固体方程和流体方程分别采用Newmark－β隐式时间积分和α－隐式时间积分方法，可以降低时间步长对计算稳定性的影响。此模型的计算采用ADINA求解非线性流故固耦合动力学方程的Full Newton－Raphson迭代方法，时间步长对收敛性有很大的影响，但是选择合适的的力松弛因子和位移松弛因子可以提高数值计算收敛的稳定性。

Newton－Raphson迭代法中线性化方程系数矩阵的条件数对其求解的稳定性和效率有很大的影响，过大的条件数会导致计算机产生舍入错误而中断计算。可以通过网格优化、采用合适的单元制和无量纲化，使系数矩阵的中最大和最小的对角元素之比不大于1011，以降低其条件数。这对本模型中采用的将固体模型和流体模型矩阵装配到一起的直接耦合求解法尤为重要。

3．2 模拟计算结果分析

3．2．1 模型的验证

为了验证此流固耦合模型的正确性，对模拟的计算结果与由试验得到简化模型的计算结果进行了对比。图5给出了这两种模型在El Centro波作用下得到位移时程，可以清楚得看到两条位移时程曲线吻合较好，其中简化模型对于结构顶点位移峰值的控制效果为20．9%，流固耦合模型对结构顶点位移峰值控制效果达到了22．4%，可见TLD对结构振动的控制效果也是十分接近的，说明此流固耦合模拟效果是具有相当的可信度的。另外从图中可见，两种模型的反应时程存在着一定的相位差，这是由于简化模型中的弹簧单元和流固耦合模型中的水单元这两种材料对结构振动的敏感度不同所造成的，但这并不会改变TLD的基本特性。

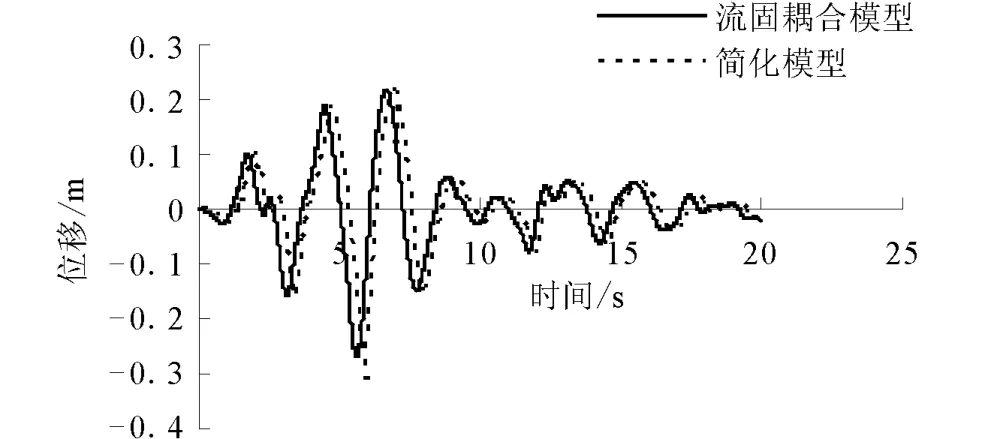
图5 简化模型与流固耦合模型计算结果的比较Fig．5 Comparison of Displacement time history at the top of storey between the simplified model and the fluid－structure interaction model

3．2．2 TLD的流场变化特性

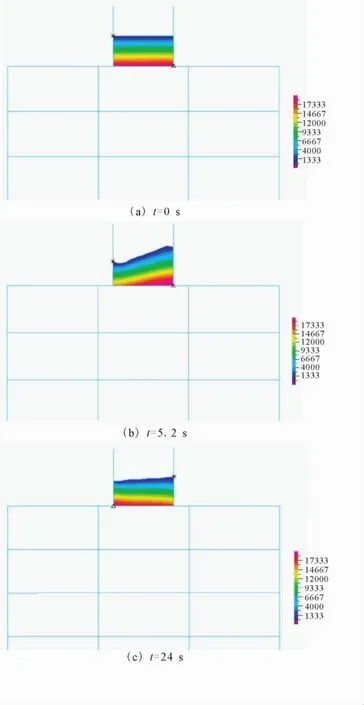
图6 输入EI（entro波）不同时刻流体的压力场Fig．6 The fluid pressure field at different time under E1Centro wave

流体作用在水箱壁上的作用力是通过对耦合面上结构节点附近的液体应力进行积分得到的，压力场直接决定了水箱壁受到的流体作用力。图6分别是流固耦合模型在El Centro波作用下不同时刻液体的压力场，其中图6（a）为结构刚开始振动时的压力场，图6（b）为结构振动过程中某一时刻的压力场，图6（c）为振动幅值最大时的压力场。

从图中可以看出，结构刚开始振动时，由于振动的幅值较小，所以流体的压力场也比较均匀；随着结构振动幅值的增大，压力场逐渐呈现局部不均匀性，并且这种不均匀性会越来越明显，最终形成局部压力集中。产生这种局部不均匀性的原因是由于晃动的流体作用在水箱壁上后，其流动方向发生了改变，形成了“驻点”效应，引起局部压力增大，即图8压力最高区域，而远离晃动方向的流体呈现低压力状态。流场的变化对结构的振动程度是一一对应的，这充分体现了流体与结构之间的耦合作用，也就是说流场变化越强烈，流体晃动对结构的反馈就越显著，从而实现了水箱对结构振动的控制作用。

3．2．3 TLD对结构的减振特性

由前面的对TLD流场特性的分析知道，流体的晃动对结构的减振在很大程度上起到了有利的作用。同时根据振动理论，当流体的晃动频率与结构的自振频率相调谐时，可以增大流体晃动幅度。处于对这方面的考虑，特对水箱的尺寸和水深进行了调整，调整后的水箱晃动频率与结构的自振频率比达到了0．96。另外，由于流体对结构耦合作用是通过流体晃动时产生的惯性力形成的，所以取一个合适的质量比也是很重要的，本文取的质量比是4．13%。

表1给出了输入三种地震波利用调整后TLD进行振动控制时，结构顶层受控前后加速度和位移的结果比较。由表中的结果可得：TLD在这三条波的作用下对结构都起到了不同程度的减振作用，尽管在减振率上确实有所差异，但即便是减震率最低的Taft波，其减震效果也达到了22．4%，还是非常理想的。由此可以得出，频率比、地震动、质量比这三个因素在不同程度上影响TLD对结构的减振性能，其中影响最为显著的是频率比。

通过以上分析，我们可以发现，经过适当设计的TLD可以充分发挥其对结构的减振特性。

表1 结构顶层受控前后加速度和位移的结果对比Table 1 The analysis results of top floor of the structure with TLD

5 结语

本文探讨了带调谐液体阻尼器结构的流固耦合有限元分析方法。这种方法有效的模拟结构与调谐液体阻尼器之间的流固耦合作用，较为准确的预测了调谐液体阻尼器对结构的减振特性及其流场的变化特性。这种方法减小了对实验测试的依赖性，并对调谐液体阻尼器的工程应用具有一定的指导意义。

［1］ 李宏男，闫石，贾连光．利用调液阻尼器减振的结构控制研究进展［J］．地震工程与工程振动，1995．15（3）：99－110．

Hong－nan LI，Shi YAN，Lian－guang JIA．Review of current researches on structural vibration control by using tuned liquid damper［J］．Earthquake Engineering and Engineering Vibration，1995，15（3）：99－110．

［2］ 梁启智，熊俊明，黄庆辉．调谐液体阻尼器对高层建筑和高耸结构动力反应控制研究综述［J］．世界地震工程，2002，18（1）：56－64．

Qi－zhi LIANG，Jun－ming XIONG，Qing－hui HUANG．A review on dynamic response control of tall buildings and high－rise structures by tuned liquid damper［J］．World Information On Earthquake Engineering．2002，18（1）：56－64．

［3］ 吴波，李惠．建筑结构被动控制的理论与应用［M］，哈尔滨：哈尔滨工业大学出版社，1997．

［4］ 李宏男，贾影，李晓光等．利用TLD减小高柔结构多振型地震反应的研究［J］．地震工程与工程振动．2000；20（2）：28－33．

LI Hong－nan，JIA Ying，LI Xiao－guang．Study on Vibration Control Using TLDs for Multi－mode Responses of Tall flexible Structures［J］．Earthquake Engineering and Engineering Vibra－tion，2000；20（2）：28－33．

［5］ 贾影，赵林，李之富．高层建筑利用TLD减小风振反应的研究［J］．地震工程与工程振动．2003，23（1）：72－86．

JIA Ying，ZHAO Lin，LI Zhi－fu．Research on Wind－induced Vibration Control Using TLD for Tall Building［J］．Earthquake Engineering and Engineering Vibration，2003，23（1）：72－86．

［6］ 欧进萍，张微敬．高层建筑结构的风振阻尼控制分析与设计方法［J］．建筑结构学报．2003，24（6）：76－89．

OU Jin－ping，ZHANG Wei－jing．Analysis and Design Method for Wind－induced Vibration Passive Damping Control of Tall Buildings［J］．Journal of Building Structures，2003，24（6）：76－89．

［7］ ADINA R＆D．ADINA理论与建模指导报告 ARD01－9［R］．USA：2001：235－262．

［8］ Bath K J．Finite element procedures［M］．Englewood Cliffs，NJ：Prentice Hall，1996：768－836．

［9］ Bath K J，Zhang H，Ji S．Finite Element Analysis of Fluid Flows Fully Coupled with Structure Interactions［J］．Computers and structures，1999，72：1－1．

［10］ 吴小峰，孙启国，狄杰建．抗震分析反应谱法和时程分析法数值仿真比较［J］．西北地震学报，2011，33（3）：275－278．

WU Xiao－feng，SUN Qi－guo，DI Jie－jian．A Numerical Simulation Comparison between Response Spectrum Analysis and Time History Analysis［J］．Northwestern Seismological Journal，2012，2011，33（3），275－278．

［11］ 谢异同，盛涛，袁俊．拟合多阻尼比目标反应谱的告精度地震动调整方法［J］．西北地震学报，2011，33（3），223－228．

XIE Yi－tong，SHENG Tao，YUAN Jun．A Modification Method of Earthquake Ground with High Precision from Fitting the Multi－damping－ratio Target Spectrum［J］．Northwestern Seismological Journal，2011，33（3），223－228．