页岩饱和含气量的计算及应用

冀 昆，毛小平，凌 翔，范家伟

(1.中国地质大学能源学院，北京 100083;2.中国地质大学海相储层演化与油气富集机理教育部重点实验室，北京 100083;3.长江大学石油工程学院，湖北 荆州 434000)

引 言

我国页岩气的资源调查和勘探开发还处在探索起步阶段。伴随着我国页岩气勘探的深入，对于在含气量计算方法方面研究的薄弱也逐渐凸显。而页岩含气量对页岩储层评价，有利区优选具有重要的意义。现有的预测含气量的方法有现场解吸法、测井解释法、TOC拟合法等。现场解吸法是测量页岩含气量最直接的方法，由于取心存在气量损失和解吸时无法准确模拟地层条件，估算量一般偏小。现代测井技术手段能够获得页岩的孔隙度、含气饱和度、矿物组成、地层温度、地层压力等参数，测井解释法求取页岩含气量可以利用储层孔隙度及含气饱和度计算游离气含量。TOC拟合法是在确定TOC是影响含气量的主导因素后，根据TOC的含量与含气量进行线性拟合，但因为忽略了其它影响因素，误差较大。以上方法在确定页岩的含气量时，获得的含气量值差别较大，给利用含气量进行资源储量的预测和有利区的优选带来困难。若把页岩储层看作物理化学性质一定的地质体，则它所能储存的气体的量是有限度的(见图1)。这个最大限度既是指页岩内游离气量和吸附气量在储层的温压条件下所能达到的最大值。如果能预先估算出页岩含气量在理论上所能具有的最大值，综合储层的非均质性、构造运动以及抬升剥蚀等因素对页岩储气性能得影响，就能较准确的估算出页岩储层真实的含气量。

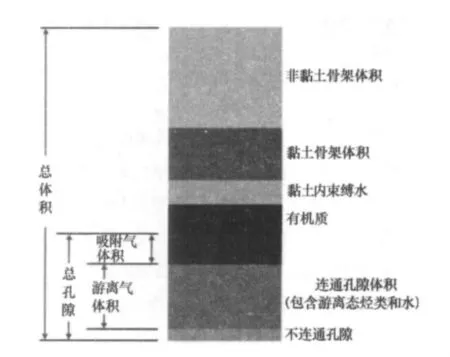
图1 页岩的岩石物理模型示意图(据Ambrose等，2010)

游离气的最大理论值即是假设储层内假设所有孔隙、裂隙空间在储层的压力和温度条件下被气体充满时的游离气量。计算游离气量的关键参数储层平均孔隙度应结合所有的岩心测试数据和测井解释数据综合判断。鉴于页岩中大量的纳米级孔隙，最后所求得的游离气量要根据吸附相体积进行校正。吸附气的最大理论值是指当孔隙和裂隙内壁(多为有机质和粘土矿物的表面)被气体分子占满时所具有的吸附量(不一定是单分子层吸附)。当储层温度不高并且吸附数据丰富时，可以结合实验室等温吸附实验和L angmuir方程来预测储层温度和压力下的最大吸附量。但现有等温试验大部分都集中在60℃ 和30℃。当评价区泥页岩埋藏较深，储层温度大部分都超过实验室等温实验允许温度。这时候可以利用Polany i吸附势理论建立吸附量与温度压力的综合关系模型来预测储层温度压力条件下页岩的最大理论吸附能力。

1 页岩游离气量最大理论值的确定

游离状态的页岩气存在于页岩的孔隙或裂隙中，其数量的多少决定于页岩内的孔隙裂隙空间。在泥页岩生气过程中。粗略估计评价区内单位体积岩石平均孔隙和裂隙空间，考虑到在地层温度和压力下的气体状态，可以粗略估算出游离气量。计算孔隙空间主要有两种方法，直接用岩心测试数据求孔隙度和通过测井解释求取孔隙度。在实际运用的时候，孔隙度的值应该由两种方法综合决定。

岩心的测试数据可以直接给出岩心的平均孔隙度和平均含气饱和度。测井解释的结果也可以大致确定评价区泥页岩层段的孔隙度和含气饱和度。首先建立孔隙度(Φ)与测井曲线值声波时差 Δt、中子 CNL、密度 DEN的一个关系式如下:

其中:a、b、c、d为待确定的适合本地区的参数，由实测孔隙度资料、测井数据、利用多元统计分析，分别进行拟合，求解公式中 a、b、c、d等参数。其次利用测井曲线计算含水饱和度，再计算含气饱和度，最后代入前述公式计算游离气量，见公式(2)。

式中:Sw为岩石含水饱和度，%;

Sg为含气饱和度，%;n=2;

a，b都为与岩性有关的系数，可通过实验测得:Rw=0.3Ω·m;

Rt为岩石真电阻率，缺少的Rt数据可以用LLD代替。

最后结合岩心测试和测井解释得到的孔隙度和含气饱和度，估算出评价区的平均孔隙度和含气饱和度后。最后考虑储层内温度和压力的条件，就可以计算出游离气含气量的最大理论之，见公式(4):

式中:G游为游离气含量，m3/t;

Φ为实测孔隙度，%;

Sg为实测含气饱和度，%;

ρ为含气岩石密度，t/m;

Bg为体积系数，Bg采用下式计算:

其中，Z－天然气压缩因子，在0.2～1之间，无量纲;t－评价层段现今地温，℃;p－评价层系所处地层压力，MPa，与埋深z有关近似地可取静水压力 p=0.01*z，可根据情况在超压段系数可以近似增至0.01～0.015之间。

2 游离气量的校正

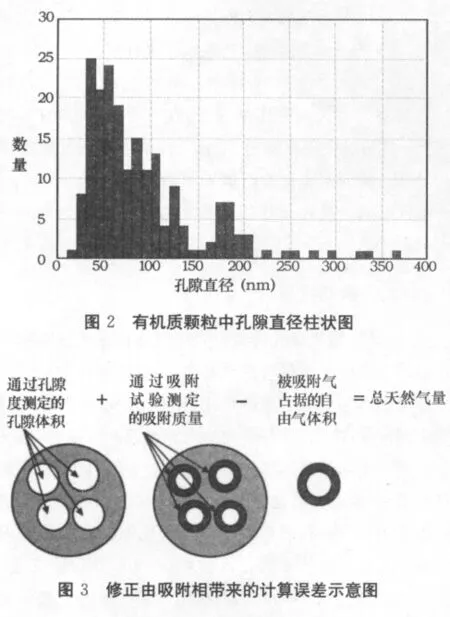
页岩中，纳米级孔隙是页岩中气体储存主要场所和运移的主要途径。尽管在页岩中，裂缝也被认为对烃类的储存和运移起着重要的作用，但在 Barnrtt页岩的研究中即使采用了各种各样的放大和显微研究技术，也仅仅发现一条未被充填的天然微裂缝。大部分情况下，裂缝呈胶结状态，尤其是在富含碳酸盐岩的泥岩中。而纳米级孔隙分为有机质质粒间纳米级孔隙和有机质粒内纳米级孔隙，其中又以有机质粒内纳米级孔隙为主。Barnett泥页岩中复合粒内有机纳米级孔隙的直径很少能达到1μm，单个粒内纳米级孔隙的平均值范围为(20～185)nm，其中粒度中值的范围为(15～60)nm(见图2)。在页岩孔隙内，一部分甲烷以物理吸附的方式形成吸附相存在与孔隙内表面。鉴于气体分子直径与孔隙直径在一个数量级上，因此在吸附相的体积对孔隙内总体积的占有比例不可忽略，对计算游离气的体积存在较大影响。因此，在计算游离气含量时，用于储存游离气的总孔隙空间应减去吸附相的体积，才等于实际上用于储存游离气的空间(见图3)。处在吸附状态的甲烷，比处在游离状态的甲烷相比体积要小得多。目前采用的最多的是 J.Sommen等人提出的吸附体积的计算公式:

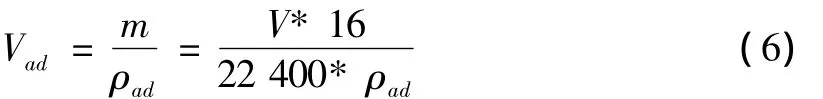
式中:Vad－平衡条件下吸附相体积，cm3*g－1;

m－吸附相气体质量，g;

ρad－ 吸附相密度，g/cm3;

V－测得的平衡条件下的气体吸附量，cm3;

关于吸附相密度的讨论见文献，在实际计算吸附相密度中运用较多的时公式(3)，可见吸附相密度主要受温度的控制。

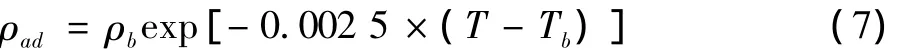
式中:ρb－沸点下甲烷密度，为0.142 4 g/cm3;

Tb－甲烷沸点温度，为111.15 K。

3 页岩吸附气量最大理论值的确定

在页岩储层中，吸附气是页岩内另一主要的气体储存形式。页岩的吸附能力介于煤层(吸附气量大于85%)和常规圈闭气(吸附气通常为0)之间。

通常用来求取气体吸附量的吸附理论主要有朗缪尔单分子层吸附理论、波拉尼吸附势能理论、BET多层吸附理论(见多分子层吸附)、二维吸附膜理论和极化理论等。在煤层气中，在描述和预测气体吸附中运用较广泛的是朗缪尔单分子层吸附理论和Polanyi吸附势能理论。这两种理论基于不同的假设。Langmuir等温吸附方程来可以准确描述确定温度下的等温吸附曲线。当储层温度范围与等温吸附实验温度相差不大时，可以利用Langmuir等温吸附方程来计算评价区页岩在该温度压力范围下最大的理论吸附量。但考虑到现在大多数等温吸附试验温度是30℃，并且远我国页岩储层普遍埋藏较深温度较高。这里选用在煤层气中运用较广泛的Polanyi吸附势能理论来求建立吸附量对温度和压力的关系模型。从而能够由一组等温吸附数据来求取储层温压条件下吸附量。

3.1 利用Langmuir理论建立吸附模型

实验证明泥页岩的吸附过程符合 Langmuir等温吸附方程，吸附的过程和吸附量可以通过Langmuir等温吸附方程来加以描述和预测。因此在储层温度较低、实验

式中:V－吸附量，m3/t;

VL－为Langmuir体积，代表最大吸附能力，m3/t;

P－压力，MPa;

PL－为Langmuir压力，Langmuir体积的一半所对应的压力，MPa。

若对公式(8)加以简化，以便用更直观的图形表示和计算。公式(8)可以写成 P/V=b+aP。其中，a代表1/VL;b代表PL/VL。以 P/V为纵坐标，P为横坐标，则该方程为一直线形式，更加便于数据的处理。带入等温吸附的数据，拟合的直线的斜率可以求得参数a、b。带入储层压力值，就可以求得该岩心在储层压力温度条件下，理论上吸附量的多少。

运用Langmuir理论建立吸附模型的一个缺点就是现有实验条件允许的最大压力不超过12 MPa，实验温度不超过100℃，而实际的地层压力和温度要远远超过这个数值。不仅如此，随着埋深增加，储层温度和压力是一个动态变化的过程。如需再预测吸附量，需做大量不同温度下的等温吸附试验，这显然是不现实的。因此，等温吸附试验在固定的温度下测得的吸附数据难以体现储层中页岩吸附的真实情况。在确定在储层温度压力条件下尤其是埋藏较深的页岩吸附量的大小时，我们需要运用新的手段确定在压力和温度双重因素影响下页岩吸附量的变化规律。

3.2 利用Polanyi吸附势理论建立吸附模型

前人在研究温度、压力双因素同时变化时，固体吸附量变化规律上曾有过研究。kim曾将温度作为吸附的变量之一，但是只是提出了一个经验公式。钟玲文等人用多个温度下的等温吸附试验，发现在不同压力下，温度和吸附量呈线性关系。建立了深部煤层气含气量的预测方法。赵志根等人也利用不同温度下的等温吸附试验，建立了饱和吸附量和温度之间的关系。胡涛在研究固－气吸附体系的时候，提出用吸附热来预测其它温度下的吸附量。虽然预测结果较为理想，但是该算法至少需要两个温度点的吸附数据。

Polanyi吸附势理论假设分子间的作用力为伦敦色散力，吸附势与温度无关，即吸附势与最大吸附量对应的曲线在任何温度下都一样(见图4)。因此可以以此为桥梁求取不同温度下的吸附量。吸附势理论已经在煤层条件允许的情况下，可以通过模拟储层温度下的等温吸附实验来直接确定吸附气量。气领域有较多的发展和应用。页岩气和煤层气有许多相似之处，下面将用吸附势理论建立起吸附量与温度压力的关系模型。

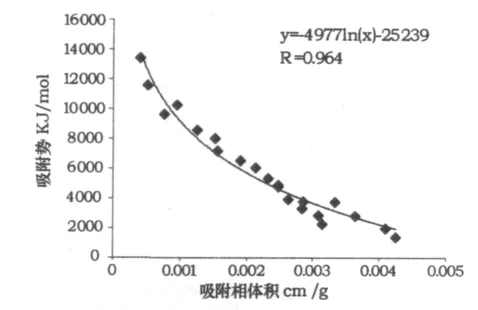
图4 某页岩样品在30℃、60℃和90℃下吸附特性曲线

建立吸附势理论模型首先要求取吸附特性曲线。吸附特性曲线由吸附势和吸附相体积两个坐标组成。固体表面某点的吸附势定义为1 mol气体从引力不起作用的气相被吸引到吸附相的某点所做的功。具体计算见公式(9)。

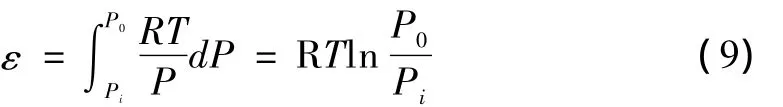
式中:P－平衡压力，MPa;

ε－吸附势，J/mol;

P0－甲烷饱和蒸汽压力，MPa;

Pi－理想气体在恒温下的平衡压力MPa;

R －普氏气体常数，取值8.314472 J/(mol.K);

T－绝对温度，K。

吸附特性曲线的另一个参数就是平衡条件下的吸附相体积，见公式(6)。但在实际储层中的温度远大于其临界温度，气体不能被液化，处于超临界状态，也就不存在公式(1)中的饱和蒸汽压。前人们提出虚拟饱和蒸汽压来代表处于超临界状态气体的饱和蒸汽压。这时饱和蒸汽压是能使特征曲线的一个参数，并没有特定的物理意义。最常用的Dubinlin提出的计算虚拟饱和蒸汽压公式。

吸附势与吸附相体积的关系为对数关系(见图4)，可用公式(11)表示这一类曲线的大致形状。其中参数a、b的值可由拟合出的表达式求得(见图4)。结合吸附势的表达式公式(1)，可得到方程(12)。联立表达式(6)、(10)、(12)，经过整理后得到吸附量与温度、压力的关系式(13)。由公式(13)只需由一组等温吸附数据，就可以求得吸附势曲线及其表达式，得到参数a、b的具体值，也就可以得到吸附量与温度压力的关系式。

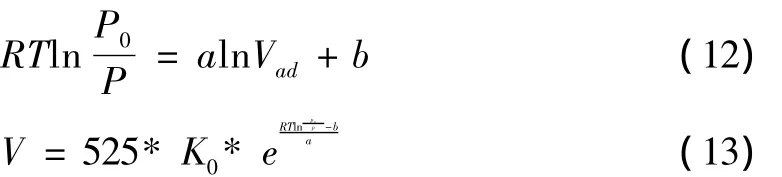
凭借该模型，仅用一个温度下的等温吸附数据求出参数a、b的值，就能预测任意温度压力下的吸附数据。但在验证模型的时候发现，模型在压力增高的时候，模型预测值与真实测量值间的差距增大。

4 以岩心为例计算饱和含气量及其值的应用

岩心作为物理化学性质稳定的地质体，所能存储的气体量是一定的。在这点上与评价储层规模的地质体是一样的。不同的是后者需要充分考虑三个方面的问题。

1)在用这种方法估算评价区的页岩的含气量时，首先在收集数据方面要充分考虑孔隙度、矿物含量、页岩等温吸附曲线性等参数在横向和纵向上的非均质性。收集的参数应做趋势面分析，筛选出区域性背景分量，使其能尽量代表评价区的整体性质。

2)应充分考虑成藏后构造运动和抬升剥蚀作用对页岩气藏储集能力的破坏。建议对比北美已开发的页岩气田构造破坏的程度和规模，为评价区设立破坏参数K(0～1)，来量化所有破坏因素对含气量的影响。计算实际含气量时，可以用理论最大含气量乘以破坏参数K值。

3)在有机质和粘土矿物对页岩的吸附作用中，有一部分吸附位是被水分子所占用的。因此在实际运用中应充分考虑水分子对页岩吸附能力的负面影响。

用来验算的页岩岩心样品采自江汉石柱地区侏罗系深度为590 m ～610 m处。该地区以滨浅湖－半深湖沉积为主。样品的基本数据(见表1)。储层压力大概为7 Mpa，温度为 60℃。经计算，游离气含气量大致为 0.6 m3/t。吸附气量在计算时，因样品埋藏较浅，因此可以在实验室做出储层温度下的等温吸附实验，(见图5)。另外经30℃ 等温吸附曲线，用吸附式定理可以推出60℃下的吸附数据(见图5)。两种方式获得的吸附数据在低压时较为一致，但在高压时有较大差值。两种方法在储层压力时吸附数据较为一致，都为1.1 m3/t。因此，经计算，该样品所能容纳的最大气体量为1.7 m3/t。其他计算含气量方法中，运用解吸法得到的含气量值为0.8 m3/t。可见，各种因素对储层的成藏后的破坏作用较大，破坏参数K应为0.4左右。

表1 样品基本资料

图5 样品在60℃时预测值与实测值

5 结论

1)若把页岩储层看作物化条件稳定均一的地质体，则其所能容纳的气体量是有限的。即游离气量和吸附气量都有其上限。综合考虑后期构造运动、抬升剥蚀以及地下水对含气量的负面影响，将最大理论含气量值乘以破坏系数K，可以得到具有实际意义的含气量值。

2)在计算游离气量最大理论值的时候，其关键参数孔隙度和含气饱和度有两种途径获得:岩心的测试数据和测井解释数据。建议综合分析比较这两种方法获得的参数值。另一点需要注意的是要充分考虑孔隙度、矿物含量、页岩等温吸附曲线性等参数在横向和纵向上的非均质性。收集的参数应做趋势面分析，筛选出区域性背景分量，使其能尽量代表评价区的整体性质。由于页岩中大量的纳米级孔隙的存在，最后要结合吸附相的体积对游离气量进行校正。

3)吸附气量的计算可根据实际情况选取 Langmuir和Polanyi两种吸附理论建立的吸附模型进行计算。若储层埋藏较浅温度较低，可以利用储层温度下的等温吸附实验结合Langmuir方程进行计算。若储层埋藏较深，等温吸附数据不易获得，可以根据低温下的等温吸附数据结合根据Polanyi吸附势理论建立的吸附量与温度压力的关系模型进行预测。该方法的有效性已经在煤层气的研究中得到应用。

［1］刘德华，肖佳林，关富佳.页岩气开发技术现状及研究方向［J］.石油天然气学报，2011，33(1)：119 －123.

［2］黄强，石元会，叶应贵，等.鄂西渝东地区吴家坪组页岩气实钻特征及潜力分析［J］.石油天然气学报，2011，33(2)：108 －112.

［3］WAECHTER N B，HAMPTON G L，SHIPPS J C.Overview of coal and shale gas measurement：field and laboratory procedures［C］.//2004 International Callbed Methane Symposium，May 2004，Tuscaloosa，Alabama，USA.Tuscaloosa：The university of Alabama，2004.

［4］BOEKER K A.Barnett Shale gas production，Fort Worth Basin：issues and discussion［J］.AAPG Bulletin，2007，91.

［5］杨小兵，杨争发，谢冰，等.页岩气储层测井解释评价技术［J］.天然气工业，2012，32(9)：33 －36.

［6］顾惕人，朱步瑶，李外郎，等.表面化学［M］.北京：科学出版社，2001：275 －280.

［7］薛海涛，卢双舫.烃源岩吸附甲烷实验研究［J］.石油学报，2003：45 －50.

［8］M M Dubinin.The potential theory of adsorption of gases and vapors for adsorbents with energetically non－uniform surfaces［J］.1 ChemRev，1960，60：235 － 2411.

［9］SOzawa，SKusumi，Y JOgino.Physical adsorption of gases at high pressures(IV)：An improvement of the Dubinin－Astakhov adsorption equation［J］.Colloid ＆In－terface Science，1976，56：83－ 911.

［10］David N.Dewhurst，Yunlai Yang，Andrew C.Aplin.Permeability and fluid flow in natural mudstones［M］.The Geological Society of London，1999.

［11］钟玲文，郑玉柱，员争荣，等.煤在温度和压力综合影响下的吸附性能及气含量预测［J］.煤炭学报，2002，27(6)：581 －585.

［12］赵志根，唐修义.较高温度下煤吸附甲烷实验及其意义［J］.煤田地质与勘探，2001，29(4)：29－30.

［13］胡涛，马正飞，姚虎卿.吸附热预测吸附等温线［J］.南京工业大学学报，2002，24(2)：24 －38.

［14］李武广，杨胜来，殷丹丹，等.页岩气开发技术与策略综述［J］.天然气与石油，2011，29(1)：34－37.

［15］李世臻，乔德武，冯志刚，等.世界页岩气勘探开发现状及对中国的启示［J］.地质通报，2010，29(6)：918－924.

［16］Julia F.W.Gale，Robert M.Reed，Jon Holder.Natural fractures in the Barnett Shale and their importance for hydraulic fracture treatments［J］.The American Association of Petroleum Geologists，2007.(4)：603 －622.

［17］Kim A G.Estimating methane content of bituminous coalbed from adsorption data［J］.US Bureau of Mine Report of Investigations，1977，8245.