基于Workbench的高速电主轴动力学特性分析
巩丽琴,贾育秦
(太原科技大学 机械工程学院,山西 太原 030024)
0 引言
高速电主轴在精密和超精密机床中具有广泛的应用[1]。高速电主轴作为加工中心等高档数控机床的关键部件,其性能的好坏直接影响到零件的加工精度,因此很有必要对电主轴进行详细的动态分析。本文将运用Workbench分析软件对某型高速加工中心的电主轴进行模态分析和谐响应分析。
1 高速电主轴有限元模型的建立
对电主轴进行简化[2],利用Pro/E建立电主轴模型如图1所示,并将该模型导入Workbench中进行网格划分,得到如图2所示的有限元模型。

图1 电主轴三维模型
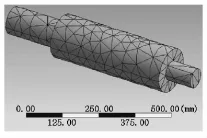
图2 电主轴有限元分析模型
2 高速电主轴的模态分析
2.1 模态分析的理论基础
系统在其任意一固有频率附近自由振动时,这种运动被称为同步运动,即模态或主振型[3]。对其结构或者部件进行固有特性分析,可为以后的谐响应分析、瞬态动力学分析以及谱分析提供必要的数据。
动力学特性分析的前提即模态分析,其结果是获得系统的自然频率和振型情况。一般来说,主轴的模态分析方程如下[4]:
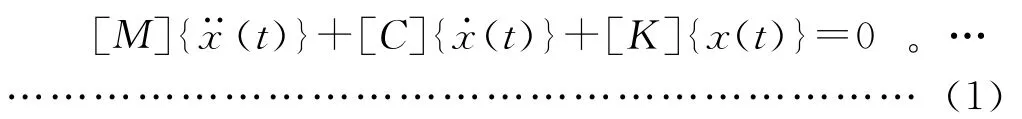
其中:[M]为质量矩阵;[C]为阻尼矩阵;[K]为刚度矩阵;x(t)为位移。从数学角度看,以上方程的广义特征值和特征向量分别对应主轴单元的固有频率和振型。
电主轴的前轴承采用定位预紧方式将其自由度全部固定,另一端轴向游动。轴向的微量位移用来补偿机床工作时主轴的热伸长[5]。在模态求解前,对电主轴固定其径向和轴向,只有切向转动。
2.2 模态分析的加载与求解
模态分析可以分为自由状态下的模态和加约束状态下的模态两种[6],还需考虑预紧力的情况。这里进行加约束状态下的无预紧力模态分析。经ANSYSWorkbench运行求解后,得到电主轴前6阶的振动特性,如图3所示。电主轴的1阶~6阶频率以及振型如表1所示。
从表1中可以看出,电主轴的前两阶固有频率相差很小,由图3可知它们为正交,可以看作重根;同理,4、5阶的固有频率也可看作是重根。
2.3 临界转速分析
当激振力的频率与电主轴固有频率相等或者接近时,轴上某些点的位移会达到或者趋近无穷大,这个频率所对应的转速就是临界转速。主轴的临界转速与固有频率的关系为:

其中:n为主轴转速,r/min;f为振动频率,Hz。计算得到的主轴临界转速如表2所示。

图3 电主轴的前6阶振型图
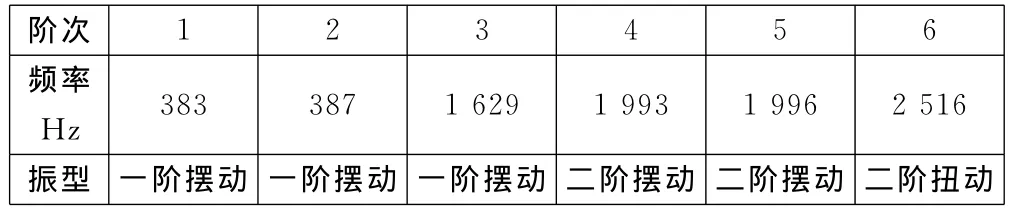
表1 电主轴的前6阶固有频率以及振型
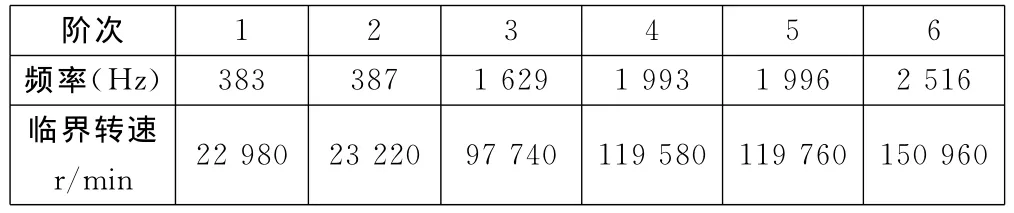
表2 高速电主轴的临界转速
本文电主轴运转的最高转速为15 000r/min,与表2中的临界转速相比较可知该电主轴的结构设计是合理的。
3 高速电主轴的谐响应分析
3.1 激振力的确定
N自由度系统的振动方程如下:
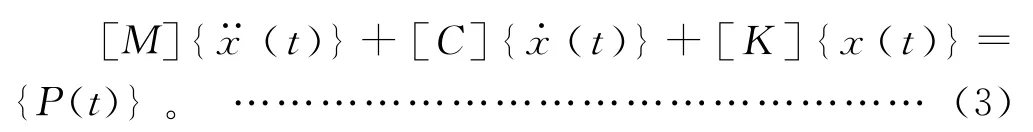
其中:[P(t)]为激阵力矩阵。
式(3)是运用有限元方法求解弹性体动力学问题的基本方程。一个完整的激振力由幅值、相位角和强迫频率组成:
P(t)=pcos(ωt+φ)。
其中:p、ω、φ分别为激振力的振幅、强迫频率和相位角。取激振力的频率为1 000Hz,振幅为2 361N,相位角近似为零。为避免结构共振,下面对电主轴进行谐响应分析[7]。
3.2 电主轴的谐响应分析
由于电主轴的固有频率从383Hz到2 516Hz,而且强制频率为1 000Hz。因此不妨取激振力的频率范围为300Hz~2 650Hz,经 Workbench求解得到电主轴前端对频率的径向位移曲线,如图4所示。
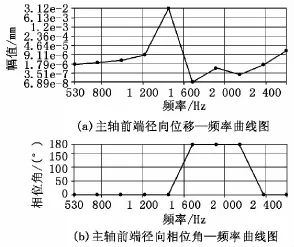
图4 电主轴前端径向位移曲线
由图4可知:当激振力的频率从530Hz增加到1 200Hz时,主轴前端处的径向位移呈增加趋势,动刚度有所减小;当激振力的频率从1 200Hz增加至1 450Hz时,主轴前端的径向响应位移迅速增加;率从1 450Hz增加至1 600Hz时,主轴前端的径向响应位移又大幅减小;在1 450Hz时位移达到最大,为31.2μm。
由图4还可以看出:当激振力的频率在3阶固有频率附近时,主轴前端径向响应位移呈增长趋势;当激振力的频率在4阶、5阶固有频率附近时,主轴前端径向响应位移呈减小趋势,主轴动刚度增加。同理,从主轴6阶固有频率附近的响应曲线可以看出,主轴前端径向响应位移仍然呈增长趋势。
主轴在强制频率1 000Hz工作时,主轴前端面的径向位移在1.79×10-3μm~9.11×10-3μm之间,此时主轴具有很好的动刚度。
对应的主轴前端面径向应力曲线如图5所示。
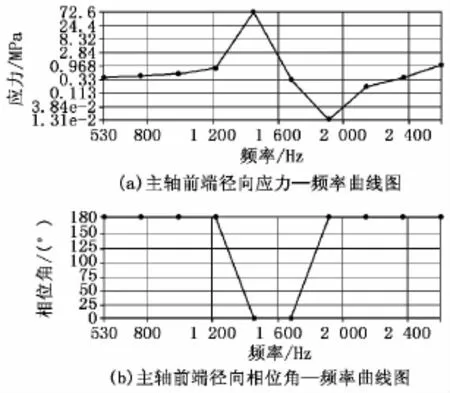
图5 主轴前端径向应力曲线
由图5与图4相对应可知,主轴前端径向位移与应力变化趋势一致,在激振力的频率为1 450Hz时,应力值达到最大,为71.57MPa。
进一步研究当激振频率位于主轴最高转速对应的频率范围内的响应特性,可以计算得主轴在最高转速时对应的频率为250Hz,所以取激振力频率范围0Hz~400Hz来分析电主轴的谐响应情况,结果见图6。
由图6可知,电主轴在低频范围0Hz~400Hz转动时,主轴前端面的径向位移不断降低;当激振力的频率达到40Hz时,位移量达到最大,为1.55mm;当工作频率为250Hz时,位移量不到49.1μm,能够满足电主轴单元工作时的精度需求。
4 总结
(1)电主轴运转时所达到的最高转速一般以不超过其一阶临界转速的75%为宜[8]。本文电主轴的转速符合这个标准。

图6 低频时电主轴前端径向位移响应曲线
(2)本文中有限元分析的思路也可以用在电主轴部件的各项设计与分析优化方面。如果对主轴关键部位进行实验数据实测,并将其与理论分析结合起来,则能够进一步提高仿真分析的精度。
[1] 巫少龙,张元祥.基于ANSYS Workbench的高速电主轴动力学特性分析[J].组合机床与自动化加工技术,2010(9):20-26.
[2] 赵跃超.HMC80卧式加工中心电主轴热、动态特性分析及耦合研究[D].兰州:兰州理工大学,2011:11.
[3] 袁金鹏.滚珠丝杠的热特性与模态分析[D].太原:太原科技大学,2012:45.
[4] 李高峰,李文斌.高速磨削机床主轴单元的动态特性仿真分析[J].机械工程与自动化,2012(4):48-50.
[5] 张俊萍,李颂华,吴玉厚.高速磨削用陶瓷轴承电主轴单元的动特性分析[J].机械设计与研究,2008(8):62-66.
[6] 张行,陶征,张安清,等.基于ANSYS的铣削电主轴静动态性能分析[J].制造技术与机床,2011(1):70-73.
[7] 周亮.电主轴热动态特性分析与研究[D].北京:北京工业大学,2010:51.
[8] 张世珍,刘炳业,范晋伟,等.电主轴设计的几个关键问题[J].制造技术与机床,2005(8):50-52.

