矩阵分解理论在数字图像处理中的应用

燕岩军

（山西机电职业技术学院，山西 长治 046011）

一、数字图像处理简介

开宗明义，数字图像处理就是用现代手段对图像进行处理。人们对数字图像都应该很熟悉。我们在计算机上看到的图像，数码相机拍到的图像，雷达图像，人体MRI图像等等都属于数字图像。数字图像处理是指用计算机对图像进行分析处理，以达到所需结果的技术。

图像处理的内容十分广泛，具体而言，可以分为：图像获取、图像增强、图像复原、图像压缩、图像分割等。这些内容都是基于矩阵的处理得到的。下面举例介绍几个重要的应用。

图像获取是图像处理的第一步。图像获取有很多方法，最常用的方法就是用传感器如数字摄像机、扫描仪等设备得到。

数字图像处理的定义：我们可以将一幅图像定义为一个二维函数f（x，y） ，这里x和y是空间坐标，在空间坐标（x，y）上的幅值f称为该点图像的强度或灰度。对于数字图像而言，x，y和幅值f都是有限的、离散的。这样一幅图像就可以用一个二维函数来表示。模拟图像不利于计算机处理，所以我们常常将模拟图像转换为数字图像。模拟图像转化为数字图像的方式是：取样和量化。我们将x，y坐标值离散化称为取样，将幅度值f离散化称之为量化。经过取样和量化的图像是一幅数字图像。数字图像的质量很大程度上取决于取样和量化的取样数和灰度级。取样和量化的结果是一个实际的矩阵。这个矩阵可以表示为

更一般的矩阵表达方式为：

图像压缩的数字图像数据压缩技术的应用，其目的是减少图像遗留在数据中的多余信息，使之得到更高效的格式存储和传输数据。可以将图象数据压缩的原因在于，数据中还有多余的信息。图像数据的冗余引起的在图像中的空间冗余，时间冗余的存在下，在不同的帧中的图像序列中，不同颜色的平面或光谱带间的相关性引起的相邻像素之间的相关性引起的频谱冗余。

图像压缩是有损数据压缩可以是无损数据压缩。无损图像压缩方法的行程长度编码，熵编码方法，如LZW，有损压缩方式主要是变换编码，诸如离散余弦变换（DCT） 或小波变换，使傅立叶变换，量化和熵编码方法压缩和分形压缩（分形压缩）。

二、矩阵的奇异值分解原理

（一）矩阵的奇异值

则特征值λi与μi之间的关系为：λi=μi＞0，（i=1，2，…，r）。

（二）矩阵的奇异值分解（SVD）

其中，△ =diag（δ1，δ2，…δr），△为奇异对角阵。U满足UH AAH U是对角阵，V满足VH AH AV是对角阵。U的第i列为A的对应于?δi奇异值对应的左奇异向量，V的第i列为A的对应于δi奇异值对应的右奇异向量。它们的每一列均为单位向量，且各列之间相互正交。

奇异值分解是一种基于特征向量的矩阵变换方法。奇异值分解是现代数值的最基本和最重要的工具之一。

三、奇异值分解的图像性质

每一矩阵的奇异值（δ，δ，…，δ）是唯一的，它12r将矩阵数据的特征与分布很明显的算了出来。一般来讲，矩阵的奇异值的分解可以作这样的一种理解：可以将矩阵当做是一种线性变换，它在根本上将m维空间的点映射到了n维的空间。通过奇异值的分解之后，该线性变换被分割成3个部分，分别为U、△和V， 其中U和V都是标准正交矩阵，因此它们相对应的线性变换，就相当于对m维和n维坐标系中坐标轴的旋转变换。

若A为数字图像，则A可视为二维时频信息，可将A的奇异值分解公式写为：

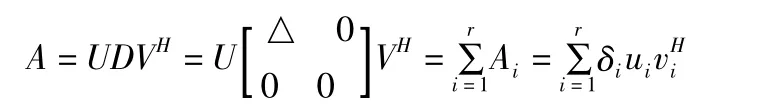
在当中，ui与vi各为U与V的列矢量，δi为A的非零奇异值。因此上述公式所表示的数字图像A可以看成是r个秩为1的子图相加的结果，奇异值?δi为权系数。所以Ai也表示时频信息，对应的ui和vi可分别视为频率矢量和时间矢量，因此数字图像A中的时频信息就被分解到一系列由ui和vi构成的视频平面中。

由矩阵范数理论，奇异值能与向量2－范数和矩阵Frobenious－范数（F－范数）相联系。

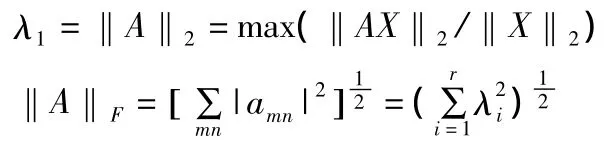
若以F－范数的平方表示图像的能量，则由矩阵奇异值分

综上所述，数字图像A在被奇异值分解之后，它的纹理与几何意义上的信息大多都集中在U、VH之中，而△中的奇异值通常代表了图像的能量信息。

性质1：矩阵的奇异值代表着图像的能量信息，因此它具有很高的稳定性。

设=A+δ，δ是矩阵A扰动矩阵的一个。A和B的非零奇异值分别记为：δ11≥δ12≥…≥δ1r和 δ21≥δ22≥…≥δ2r。且r=rank（A） ，δ1是δ的最大奇异值。则有：|δ1i－ δ2i|≤‖A－B‖2=‖δ‖2=δ1。

通过上述阐述可以得知，图像在被小的扰动所干扰的时候，扰动矩阵的最大奇异值一般情况下都大于图像矩阵奇异值的变换。因此图像奇异值的稳定性能非常强。

性质2：矩阵的奇异值具有比例不变性。

性质3：矩阵的奇异值具有旋转不变性。

设m×n，矩阵A的奇异值为 δi（i=1，2，…，r），r=rank（A） 。若Ur是酉矩阵，则矩阵Ur A的奇异值与矩阵A的奇异值相同：

性质 4：设，rank（A） =r≥s。若△s=diag（δ1，δ2，…，δs），

所以可得：

上面的方程式已经说明，通常在F－范数意义之下，As是在空间（秩为s的m×n维 矩阵构成的线性空间）中A的一个将秩最佳逼近。因此可根据需要保留s（s＜r）个大于某个阈值的δi而舍弃其余r－s个小于阈值的δi且保证两幅图像在某种意义下的近似。这就为奇异值特征矢量的降维和数据压缩等应用找到了依据。

结语：前面所有的讨论都已经表明，图像压缩通过奇异值来分解的办法是有效的，具备很好的实用价值，不过还有很多有待改进之处。

1.划分子块的划分方式上，通常采取更有效的方法来完成。例如，大型矩阵，随机抽样矩阵居较小的矩阵计算的小矩阵的奇异值，反复几次，这些小的奇异值的原始矩阵奇异矩阵逼近。

2.操作的速度的影响因素，是比较大的SVD变换操作，可以找到一个快速的奇异值分解的变换算法。

此外，如果是已知的特征空间中的图像矩阵的奇异值，一般认为，较大的奇异值和其对应的奇异向量表示的图像信号，而噪声的小的奇异值反映在和它们相应的奇异向量。选择阈值低于阈值的奇异值被设置为0（截断）是根据一定的准则，那么这些奇异值和奇异向量对应的重构图像进行去噪。考虑图像局部平稳，奇异值分解的图像块消噪保持边缘细节，所以在一定程度上。如果你仔细看，SVD去噪有方向性。据SVD图像的性质，图像块旋转SVD去噪，图像划分成不同的块，然后分别为每个图像块旋转SVD的去噪，最后的总投资组合去噪图像。因此，图像的主观质量可能已大大提高。

［1］许君一.矩阵分解及量化数字水印研究［D］.广州：中山大学，2006.

［2］张瑾，杨常清.基于矩阵分析的数字图像处理方法［J］.微机发展，2003，13（5）：35～37.

［3］RafaelC.Gonzalez，，Richard E.Woods.Digital ImageProcessing.Second Edition［M］.Beijing：Publishing Houseof Electronics Industry，2007.2.

［4］冈萨雷斯.数字图像处理.第二版［M］.北京：电子工业出版社，2007，42.

［5］旷明.关于矩阵变换的数字图形处理［J］.达县师范高等专科学校学报，2003，13（2）：15～18.