基于混沌理论的导航电文LDPC设计
北京航空航天大学电子信息工程学院 周 昀 黄智刚
一、引言
混沌是非线性系统普遍存在的现象,于上世纪60年代被Lorenz发现。混沌现象具有不可预测性、对初始条件的敏感依赖性和非周期性等特点。近年来,人们已经将混沌理论应用到通信领域,基于混沌系统固有的基本属性设计相应的扩频、保密通信等系统。如何将混沌理论应用到卫星导航信道编码中,特别是LDPC的设计中,是本文主要探讨的内容。
LDPC码由Gallager首先发明,之后MacKay等人重新研究发现在码长较大时(大于104)其性能甚至超过了Turbo码。Richardson等人基于置信传播算法,应用密度进化理论研究了LDPC码的性能,并将其用于校验矩阵的优化设计。目前LDPC已经应用于移动通信,无线局域网,以及卫星导航系统等领域。
本文首先介绍混沌系统的基本特点以及典型的混沌模型,然后利用基本模型Logistic构造一种基于混沌理论的LDPC码(称为Chaos code),将其与规则的MacKay码以及随机构造的非规则LDPC码比较,从而分析说明利用混沌理论设计的LDPC码的优缺点。
二、有关LDPC基本概念的说明
LDPC码可用非常稀疏的校验矩阵H或Tanner图来表示H的列中非零元素“1”(GF(2)域)的个数称为列重(ds),对应于Tanner图中与变量节点(symbol node)相连的边的个数;每行中“1”的个数称为行重(dc),对应于校验节点(check node)相连的边的个数。若dc,ds为固定值,则称为规则LDPC码,否则称为非规则码。非规则码变量节点和校验节点的密度分布分别定义为:

式中,λi(ρi)是指连接到度为i的变量节点(校验节点)边的个数占总边数的比例。且满足:

式中,dsmax,dcmax为相应的最大度数。设码长为n,校验位为m,则度为i的变量节点(校验节点)个数分别为


图1(a)表示一个码长为8,码率为1/2的非规则LDPC码的校验矩阵,图1(b)为对应的Tanner图。其中,变量节点度分布序列:
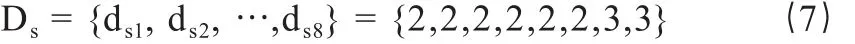
校验节点度分布序列:
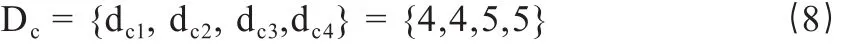
图1(a)还描述了校验矩阵H中环长等于4(s7-c3-s8-c4-s7)和6(s1-c1-s7-c3-s5-c4-s1)的环。校验矩阵中短环的存在特别是长度为4的环,影响LDPC码的译码性能。然而近期的研究表明,环长并非是影响LDPC码性能的绝对因素,环长分布对码性能也具有重要的影响。环长分布将在下文详细分析。
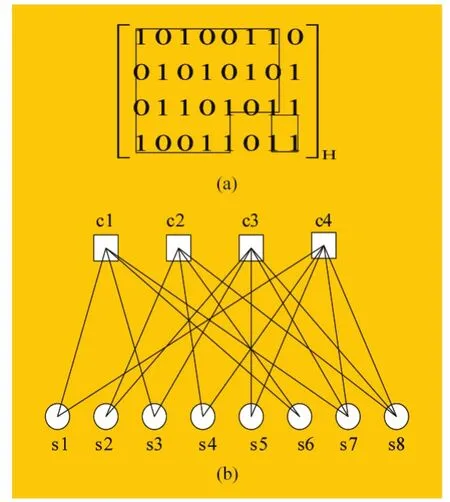
图1 校验矩阵及其对应的Tanner图
三、混沌系统的基本特性
混沌系统具有以下基本特性:
(1)有界性:混沌状态是有界的,即它的运动轨迹始终局限于一个确定的区域,即混沌吸引域。假如初始状态:0<x<L,则之后的所有迭代结果都落在此区间内。
(2)非周期和不可预测:如果在无限精确的数学层次上跟踪一条混沌轨道,经历的状态永远没有重复的,当要确定某个混沌轨道上的相点时,只能跟踪轨道的全过程,而不可能利用任何具周期意义的、有可压缩性质的所谓规律来准确预测。
(3)初值敏感性:实际中只可能以有限的精度来设置初始值,若误差以指数速度迅速增加,则计算结果将越来越依赖于表示初始条件的无理数的小数部分的位数。随着时间推移系统将变为混沌态。也就是说:初始条件的极小偏差,经过一定次数的迭代后,将会引起混沌轨迹的极大差异。Lorenz形象地把这种对初始条件的敏感依赖性称为“蝶形效应”。如果我们将不同的初始状态映射为不同的码字,那么简单来说,经过适当的迭代次数后,相应的轨迹具有宏观的距离。
下文将详细讨论如何利用混沌系统的有界性、不可预测性、初值敏感等特性设计LDPC码。
四、利用Logistic混沌模型设计LDPC码原理
一维离散时间混沌系统可以用差分方程简单描述为xn+1=f(xn)。一维离散映射通常是分段单调的,常见的有Tent映射和Logistic映射等。Logistic映射是在实际系统中存在的较简单的非线性差分方程,是一个被广泛研究的动态系统,本文后面的研究都是基于该模型的,具体表达式为

式中,λ为分叉参数,3.5699…<λ≤4时,Logistic映射表现出混沌行为。当初值0<x0<1,根据有界性,迭代序列的取值范围也一定在该区间内。设λ=4,x0=1/3(取无理数),图2中(◇)给出了迭代60次序列值,由图可以看出,混沌序列在(0,1)内无规则、杂乱无章地分布。同理为了说明初值敏感性,设λ=4,x0=1/3+10-5,画出迭代60次序列值(Δ),由图2,迭代10次以后两条初值相差1×10-5的轨迹变得完全不同,说明了该混沌系统对初值的敏感特性。
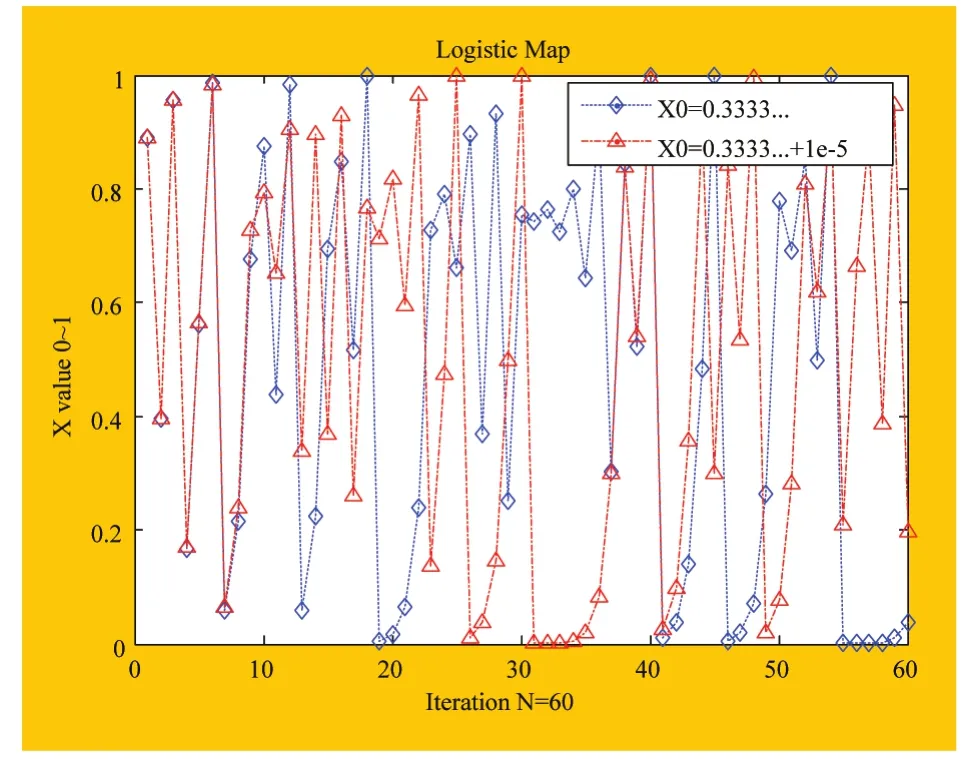
图2 Logistic映射初值敏感性
我们以序列值xn为横坐标,以其落在区间(0,1)内的个数为纵坐标,迭代1000次画出其分布情况如图3。由图3可知在区间(0,1)内序列关于0.5对称分布。
在讨论混沌行为的状态特征时,要研究时间趋于无穷后(即迭代次数趋于无穷大)对整个时间过程进行平均的极限过程,即混沌状态的概率分布密度(也称不变测度),也就是研究图3中包络情况。对于一般的混沌映射,我们用分析离散映射的有用的工具:Perron-Frobenius方程。若一维离散映射为xn+1= f(xn),则P-F方程可表示为:
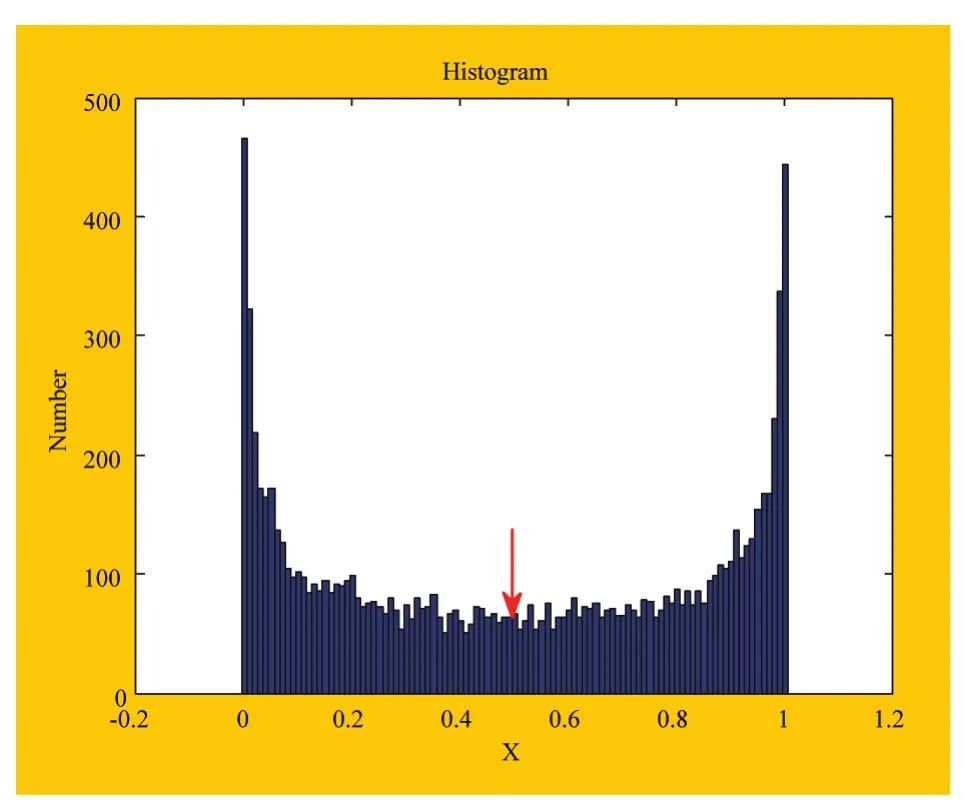
图3 Logistic映射分布直方图
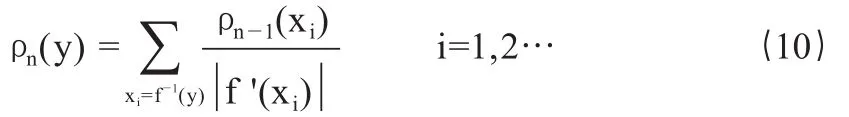
我们根据P-F方程可求得Logistic映射的概率密度分布函数:

式(11)用图4表示如下。观察知:密度函数也是关于0.5对称的,而且在0.5处取得极小值。
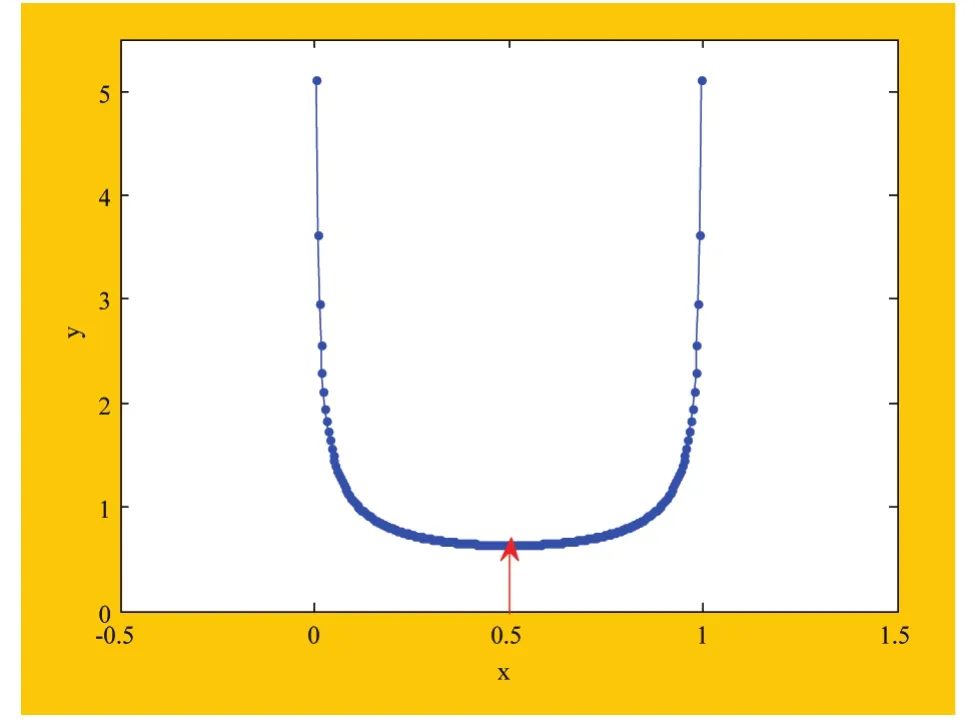
图4 Logistic映射的概率密度分布函数
综合以上研究结果,利用Logistic混沌模型设计LDPC码的校验矩阵规则如下:
(1)稀疏:根据Logistic混沌模型分布特性(图3、图4),知其在中间值密度最低,而LDPC码中非零元素稀疏分布(即“1”的个数远远小于校验矩阵的大小),我们可以将中间值在混沌轨迹中的位置,即作为元素“1”在校验矩阵中的位置。
(2)距离:在无限精确的数学层次上考虑,混沌序列具有周期无限的特性,即同一个值不可能出现第二次,反应在轨迹上即两条轨迹不可能相交。混沌系统又具有初值敏感特性(图2),初始值的极小差异,经一定次数的迭代后,导致混沌序列的值完全不同,反应在校验矩阵H中,即任意两行中“1”的位置具有距离特性。
(3)不规则:由混沌模型构造校验矩阵H,由于其值的不可预测性,体现在H中,即行、列中“1”的个数分布不均匀,也就是说利用混沌模型取值的不规则,可以构造出满足一定密度分布的非规则LDPC码。Luby,Richardson等人的研究结果已经证明,优化设计的非规则LDPC的性能好于规则的LDPC码。
根据以上规则,设计LDPC码校验矩阵具体步骤为:
第一步:产生混沌序列:设校验矩阵为hm×n,混沌序列初始值x0i,分叉系数λ=4,根据Logistic映射方程(9),迭代生成m维混沌序列xi(即迭代次数为m)。
第二步:确定h中每列1的个数和位置:统计序列xi落在区间A(0.5附近的一个区间)内的个数numi,(即为h的列重),并记录相应的位置索引indexi(即h的每列中1的位置)。
第三步:由密度演化理论构造h:根据有关文献,选取密度分布对(λ,ρ),由式(5),式(6)度为的变量节点的个数设为si。若第二步中的numi与i相等,则将位置索引indexi位置处填1,其余位置填0后构造的m×1维矢量作为h中度为i的列。
第四步:构造h下一列需满足的条件:检验该列和已构造的h中所有列,保证没有长度为4的环,即要求该列与校验矩阵中任意一列相同位置处1的个数最多是一个,公式表示就是hi和hj内积的汉明重量小于等于1。这样保证环长将大于4。
五、性能仿真与分析
考虑到LDPC码的块结构、逼近Shannon限和知识产权等因素,GPS新民用信号L1C(频点1575.42MHz),播发的导航电文CNAV-2中第2帧和第3帧分别采用码长1200,548,码率为1/2的LDPC码作为前向纠错码。在同样的码长和码率条件下,我们分别构造了三类(n,k)=(1200,600)和(548, 274)的LDPC码。利用上述混沌法构造时,尽量保证混沌序列初始值x0i为一个无理数,这样在迭代一定次数后,无理数的小数部分的微小差异会被宏观地体现出来,具体反映在序列xi落在设定区间A内的个数能更好地满足条件。对于区间A={0.48-2-8, 0.5+2-8},仿真实验表明,当A={0.48-2-8, 0.5+2-8}时最理想。至于随机构造的非规则LDPC码,在保证变量节点密度的条件下,随机搜索每列中1的位置,而且尽可能使每行中1的个数一致,同样要求不能有长为4的环。
其中混沌构造法与随机码选取一致的密度分布对。码长为1200时变量节点最大度选为15,密度分布如下:
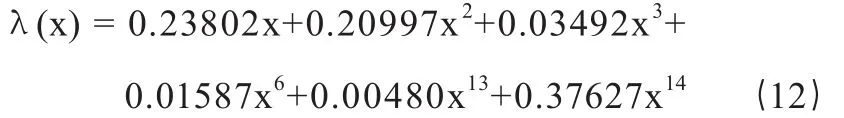
码长为548时,变量节点最大度数设为11,密度分布如下:
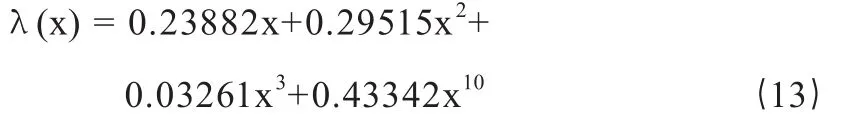
对于不同码长选取的不同密度参数具体见表1。
MacKay规则码,保证每列1的个数为3,每行1的个数为6,即ds=3,dc=6。在构造时同样要求消去长为4的环。
最后在二进制高斯白噪声信道(BIAWGN)下,仿真验证上述三种LDPC码的性能,仿真实验系统参数见表2。文中选取对数似然比置信传播算法(LLR-BP),最大迭代次数设为80次,而且对于每一个Eb/N0值,错误的帧个数达到100个则仿真结束。
图(5)和图(6)比较了混沌码(Chaos)、MacKay码和随机码(Random)在码长取1200,548时的误码率和误帧率。表(3)、表(4)则列举了误码率为1×10-5,误帧率为1×10-2条件下三种码的Eb/N0值。可以看出混沌码大约好于随机码0.1dB,好于MacKay码0.2dB。
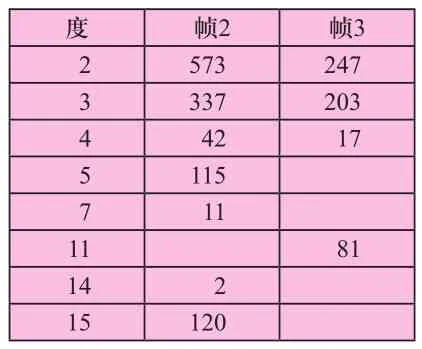
表1 密度相关的变量节点数
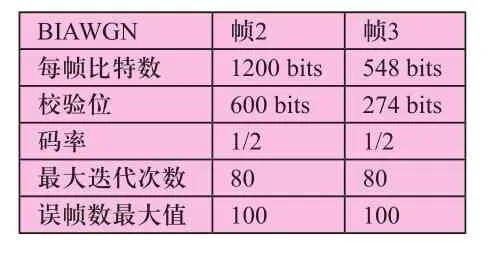
表2 仿真实验系统参数
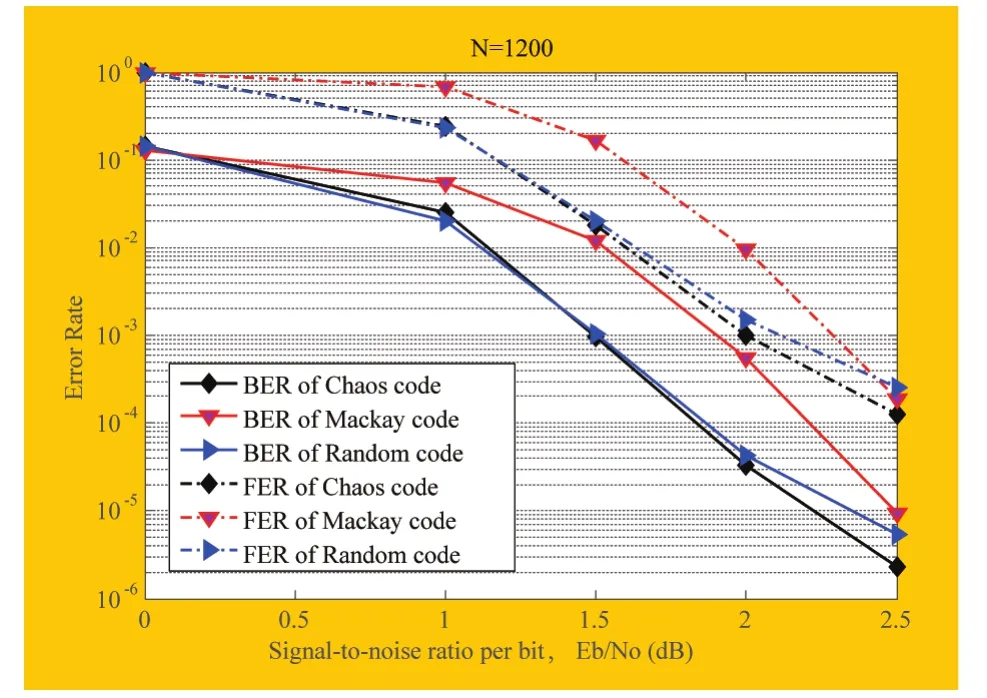
图5 BIAWGNC下码长1200误码率、误帧率
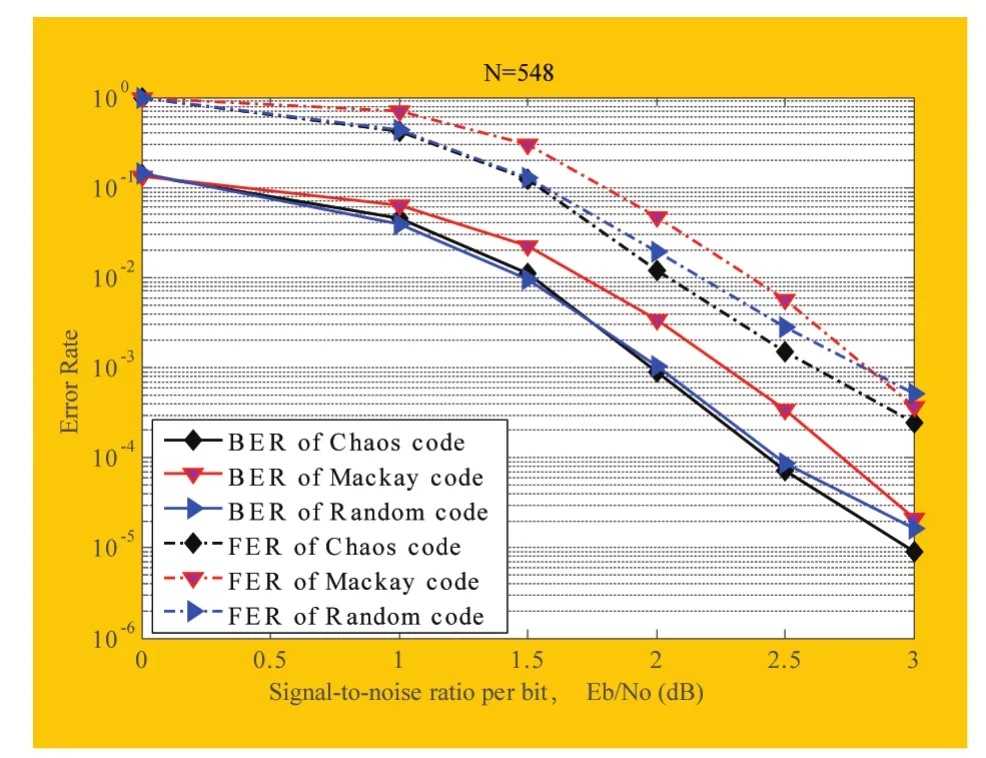
图6 BIAWGN下码长548误码率、误帧率
接下来从校验矩阵的环分布特性来分析比较三种码,本文以码长等于548的码为例说明。由表5知,规则的MacKay码中最小环长为8的变量节点数占总数的比例约41%,最小环长为6的变量节点数比例约为56%,且有16个变量节点数的最小环长大于等于8,而利用混沌构造的非规则码,其最小环长为8的变量节点数占总数的比例不到百分之一,几乎所有的变量节点其最小环长都是6,随机码也具有同样的现象。但是考虑整个校验矩阵,相比MacKay码,混沌码和随机码环的数量较多,且不同长度的环分布方差也较大。Thomas R研究结果表明:环不规则分布(即环分布方差)的影响大于环长的影响。
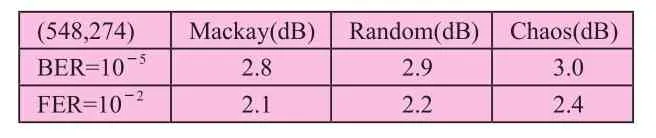
表3 码长为548时三种码性能比较
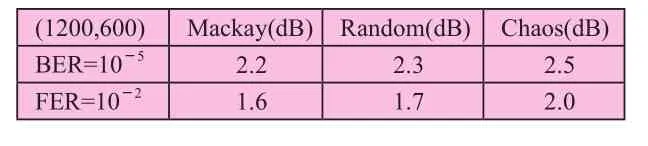
表4 码长为1200时三种码性能比较
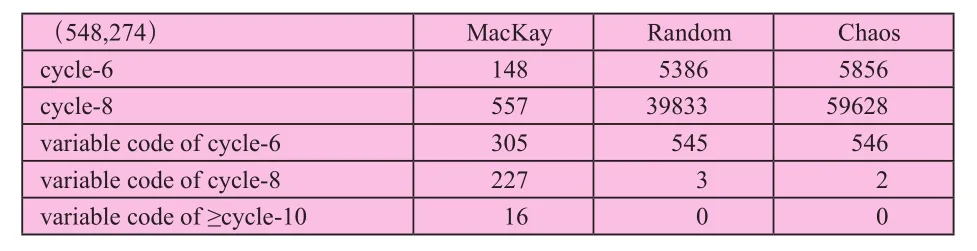
表5 码长为548时码的环分布特性比较
表6计算了环长为6和8的环的均值和方差。从三种码的环长分布特性可看出,混沌码,其环分布的方差(σ)是最大的,cycle-8时是随机码的1.6倍,MacKay码的300倍。这就从环的不规则分布特性解释了混沌法构造LDPC码的优点,即利用混沌系统的类随机、不规则以及不可预测特性可构造环分布方差较大的LDPC码,从而相比MacKay码、随机码具有更高的编码增益。
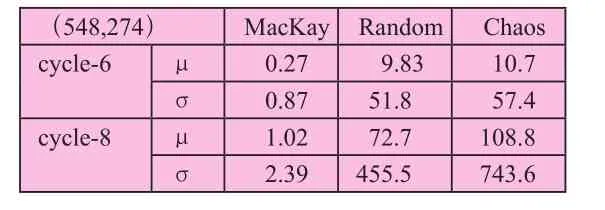
表6 三种码的环长分布特性比较
由图5、图6可以看出,尽管混沌码和随机码随着信噪比的增加会出现错误平层,但是混沌码相比随机码错误平层性能略有改善,即出现平层时的Eb/N0值较高。我们知道错误平层与最小码距直接相关,所以相比随机码,混沌码的最小码距有所改善,相比规则的MacKay码还是较小。
六、结束语
本文主要探讨了如何利用混沌系统的基本特性以及特定的混沌模型的性质来设计LDPC码。综合分析研究结果,我们得出以下结论。
(1)给出混沌模型,确定模型初值后,利用简单的迭代就可产生一系列混沌轨迹,从而有效地确定校验矩阵中非零元素的位置,结合密度演化理论,可以构造任意码长和码率的LDPC码。
(2)码长n=548/1200,信噪比区间(1~2.5dB/1~2dB),混沌构造法与随机码性能相当,优于MacKay码大约0.3dB/0.4dB;在区间(2.5~3dB/2~2.5dB),相比随机码和MacKay规则码,混沌码的编码增益改善约0.1dB,0.2dB。
(3)利用混沌理论构造的LDPC码环(cyecle-6和cycle-8)分布方差较大,相比随机码错误平层略有改善。
见www.dcw.org.cn


