汽车前保险杠系统模态分析中部件接触的研究
石 锦 杜登惠 蒋 晨 岳亮亮
(泛亚汽车技术有限公司)
1 前言
汽车保险杠系统的整体模态是其前期开发阶段需要关注的重要性能指标。若模态指标不满足要求,将在整车疲劳耐久试验或客户使用过程中出现保险杠系统结构损坏等问题。
在汽车保险杠产品设计研发阶段,因没有物理样件,所以通常采用CAE虚拟仿真来评估保险杠系统模态,预测其结构的动态特性,因而较高CAE仿真结果的置信度成为保险杠开发能力的体现。本文通过对虚拟分析结果与物理试验结果进行对比分析,合理改进CAE分析方法,进一步提高保险杠系统模态仿真结果的置信度。
2 模态分析方法
保险杠系统的模态分析方法主要有理论模态分析方法和试验模态分析方法。
2.1 理论模态分析
在实际工程中,通常采用数值方法进行理论模态分析,由于有限元法具有很强的实用性和通用性,区域离散的有限元法在众多数值方法中最受欢迎[1],因此,将采用有限元法对汽车前保险杠进行理论模态分析,求解基本原理如下。
对于具有多个自由度的系统的强迫振动方程为[2]:
式中,[M]为质量矩阵;[C]为阻尼矩阵;[K]为刚度矩阵;{x}为节点位移列阵;{f}为结构载荷列阵。
由于需要分析结构的固有特征,所以取{f}=0;同时因结构的阻尼很小,对固有频率和振型的影响可忽略不计,则无阻尼自由振动方程为:
式(2)为常系数齐次微分方程,设其解为:
式中,xM为振幅列矢量;j2=-1;t为时间;w为振动固有频率,令w2=λ。
将式(3)代入式(2),并令其有非零解的条件系数行列式必须等于零,则
由式(4)可解得特征值所对应的第i阶特征矢量 xMi,即对应于各阶固有频率 w1,w2,,…,wn,则有各阶固有振型 xM1,xM2,…,xMn。
2.2 试验模态分析
模态试验测试系统包括激励设备、传感系统和分析设备三部分。通常采用力锤作为激振,以单点激振、多点拾振来采集数据。采集的数据经过专业软件处理即可得到模态振型和频率。前保险杠系统的模态测试在整车上进行,其试验流程见图 1。
3 模态有限元分析
3.1 模型描述
采用hypermesh软件截取半车模型进行有限元建模,包括前保险杠系统、部分白车身、副车架、翼子板和大灯等,如图2所示。对于前保险杠系统的各零件,用网格准确表现其几何特征和安装孔位;由于塑料零件可能存在厚度变化的情况,根据不同几何数模分组并赋予不同的厚度。
前保险杠系统在车身侧的安装点同样是建模的关键。对于螺栓、螺钉、推钉等连接方式,各安装孔采用了两圈四边形单元模拟,以确保内圈的外径与垫片尺寸相同,并采用MPC单元连接内圈节点;对于塑料卡扣,根据搭接位置和面积选取节点并采用MPC单元进行连接;采用ACM模拟点焊,输入实际焊点的直径;采用adhesives模拟涂胶;采用共节点的方式模拟T型部位的超声波焊接。
3.2 计算结果
利用有限元软件Nastran计算前保险杠系统模态,得到第1阶频率为22.1 Hz,振型为上下方向的弯曲振动,如图3所示。由于前保险杠近似悬臂系统安装在车身前端,加之集成了许多功能件,具有一定质量,因此上下方向的弯曲振动是其主要振型之一。
4 试验模态分析
根据有限元分析结果,将三向加速度传感器布置于非低阶模态振型节点位置,并确保传感器的位置和数量可描述保险杠系统的大致外形,以测量和记录测点在整车坐标系中的位置。本文所研究的前保险杠系统中布置了30个传感器,包括车身侧4个测量点、副车架上3个测量点、蒙皮上16个测量点、下腹板上6个测量点和小腿保护杆上1个测量点,见图4和图5。
考虑到保险杠系统总成尺寸及特性,利用Maxwell互异性原理,采用锤击法输入能量,同时通过调整合适的输入能量确定系统线性范围,在系统线性范围内测得试验结果。
首次测量得到的原始状态的前保险杠系统模态试验频响结果如图6所示,可知试验的第1阶模态为28.9 Hz,为弯曲振型。虽然第1阶模态振型与有限元分析结果一致,但由于频率与有限元分析结果相差达6.8 Hz,因此需要进行试验与有限元模型对比研究。
5 有限元分析结果与试验结果对比分析
5.1 模型状态对比
通过对试验车状态、整车CAD数模及有限元模型进行检测发现,在实车中,吸能块在垂直和水平方向被紧密地挤压在前保险杠蒙皮与防撞梁之间,小腿保护杆前端也与前保险杠紧密接触;在CAD数模中,吸能块与防撞梁之间及小腿保护杆与前保险杠蒙皮之间存在设计间隙,见图7。
在设计前保险杠系统结构时,为保证部件之间的配合会留有一定间隙,以便吸收制造偏差,避免在装配过程中发生干涉,影响功能实现或造成安全隐患[3],通常吸能块与防撞梁之间的设计间隙约为5 mm。而试验车上的吸能块由于制造偏差的缘故吸收了间隙,与防撞梁密实压紧。小腿保护杆与吸能块的情况相同,在制造偏差的影响下与蒙皮发生了接触。然而由于设计间隙的存在,在初始的有限元模型中并未考虑上述接触关系。
5.2 接触对模态试验的影响
为了在试验中考查吸能块和小腿保护杆对前保险杠系统模态的贡献量,设计了2组试验:第1组试验去除吸能块,第2组试验去除吸能块和小腿保护杆。试验结果见表1、图8和图9。
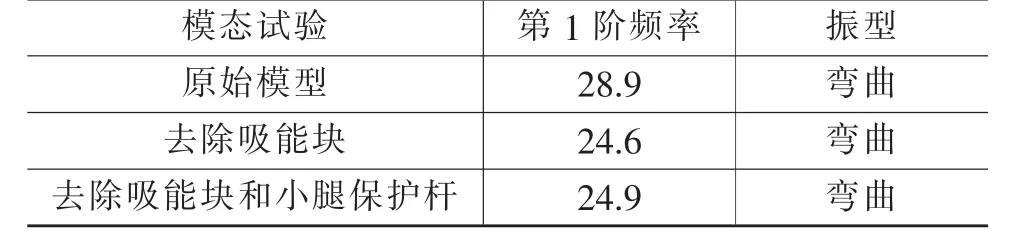
表1 前保险杠系统模态试验结果 Hz
由试验结果可知,去除吸能块后,第1阶模态频率由28.9 Hz下降至24.6 Hz,其在该车型中对前保险杠系统模态的贡献量为4.3 Hz,约占原始模型第1阶频率的15%;而去除吸能块和小腿保护杆后,第1阶频率为24.9 Hz,比仅拆除吸能块升高0.3 Hz,说明小腿保护杆对模态的贡献量为负。
5.3 接触对模态有限元分析的影响
为在有限元分析中考查吸能块和小腿保护杆对前保险杠系统模态的贡献量,采取去除吸能块与同时去除吸能块和小腿保护杆,并分别在考虑接触和不考虑接触2种情况下进行分析计算,计算结果见表2。
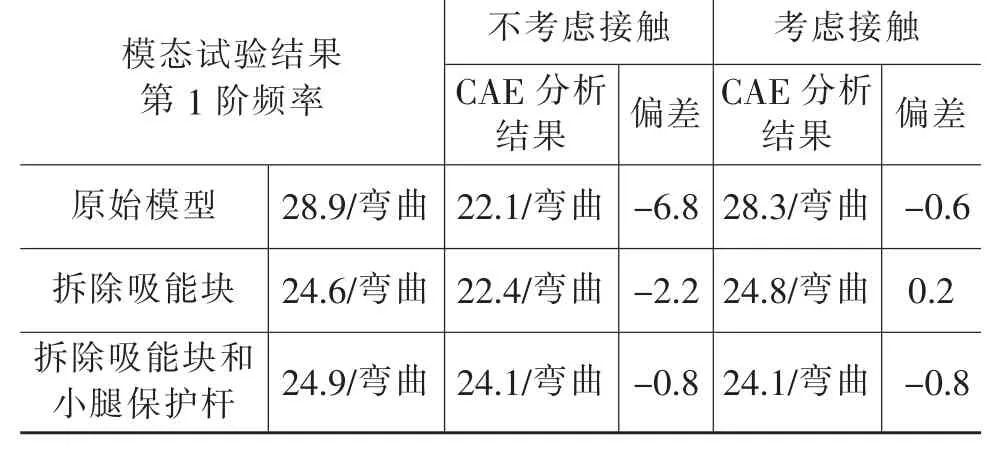
表2 前保险杠系统模态分析计算结果 Hz
由表2可知,试验结果与有限元分析结果的第1阶频率的振型均一致,为弯曲模态。当考虑接触时,频率的计算结果与试验结果吻合度较高;不考虑接触时,计算结果与试验结果相差较大。
当原始模型中未考虑吸能块和小腿保护杆与周边零件的接触时,模态计算值为22.1 Hz;当考虑接触后,模态计算值为28.3 Hz,与试验结果仅相差0.6 Hz。进一步分析吸能块和小腿保护杆对模态的贡献量,先拆除吸能块,并考虑小腿保护杆接触蒙皮,则计算结果为24.8 Hz,与试验结果仅相差0.2 Hz;然后同时拆除吸能块和小腿保护杆,计算结果为24.1 Hz,与试验结果相差0.8 Hz。
由上述可知,吸能块的接触导致第1阶模态频率上升3.5 Hz,贡献量达12.4%;小腿保护杆的接触使得第1阶模态频率上升2.4 Hz,贡献量达8.5%。由此表明吸能块和小腿保护杆在前保险杠系统中的接触关系对提高模态频率起了很大作用。
6 结束语
通过对某车型前保险杠系统模态分析结果和试验结果进行相关性分析,研究了接触在前保险杠系统模态分析中的贡献量,结果表明:
a.汽车前保险杠中部件之间的接触关系对模态结果有很大影响。在有限元模型中适当考虑吸能块和小腿保护杆与防撞梁和蒙皮的接触,可显著提高计算结果的精准度以及有限元模型的可靠性。
b.在进行模态计算结果与试验结果相关性分析时,除要检查主要零件清单及主要连接部位外,还应考虑产品实际状态与设计状态之间的差异,并据此修正有限元模型,保证分析结果与试验结果的一致性。
1 黄金陵主编.汽车车身设计.北京:机械工业出版社,2007.
2 G.R.Liu,S.S.Quek,著;龙述尧,等译.有限元法实用教程.长沙:湖南大学出版社,2004.
3 曹渡主编.汽车内外饰设计与实战.北京:机械工业出版社,2011.

