基于质量工程的大学教学团队综合评价：以广东省本科院校国家级教学团队为例

林晓新，蒋 辉，黄雅纹

(惠州学院 a.服装系;b.数学系;c.建筑与土木工程系，广东 惠州 516007)

1 广东省本科院校国家级教学团队状况

教学团队是由多位具有共同目标而相互协作的教师组成的正式群体［1］。它起源于上世纪中期的美国，后来在美国的高等学校和中小学得到迅速发展［2］。广东的大学教学团队(University Teaching Team，简称UTT)始于上世纪90年代中期，当时大多数是以“课程组或教研室为基础的课程教学团队”出现于各高校［3］。近年来，随着高等教育发展以及社会对人才培养的需要和国家宏观政策的引导，广东大学的教学组织结构发生了较大的变革，逐渐摒弃以“学校—学系—教研室”为特征的学校和院系自上而下对教师进行行政管理的传统模式，代之而推行的是以“学科”或“课程”、“课程群”为基本单元、以“二级学院(系)”为管理实体的教学团队模式。UTT建设成为政府(省教育厅)和各高等学校有组织的行政行为，师资队伍从数量到质量都有了长足的进步，推动了质量工程与教学教改水平的提升。2007年1月，教育部、财政部联合发布的《关于实施高等学校本科教学质量与教学改革工程的意见》(教高［2007］1号，简称“质量工程”)，把教学团队建设作为质量工程建设的重要内容之一，并遴选出100个国家级UTT进行支持与资金扶助。2008—2010年，国家级UTT数量分别增加到300、305和308个，涉及多个学科领域和众多所高校，组建的UTT对提高高校师资队伍水平和本科质量工程起到了重要的作用。

广东省本科院校于2007年有2个教学团队被评为国家级UTT，到2010年共发展到35个。这些国家级UTT涉及医学、农学、理学、工学、文学、史学、经济学、教育学等多个学科领域(表1)，为广东省本科院校的质量工程建设起着示范作用。为了更好地对广东省国家级UTT进行分析，课题组设计了调查问卷并进行了调查。根据2007—2009年24个国家级UTT的调查结果并对其相应10项主要评价指标数据进行量化［4］(表2)和分析，可以看出:广东省国家级UTT近年发展迅速，带头人具有先进的教育思想观念及深邃的学术造诣、多次获国家级或省部级奖励、长期致力于教学研究，在团队中起着核心与灵魂作用，能有效地带动UTT的建设;各UTT承担多项国家级、省部级教研教改及科研项目;其成员年龄、学历、职称结构基本合理，他们具有丰富的教学实践经验，符合教学团队建设工作的基本思路和价值取向。当然，这些UTT也存在一些不足，例如，规模参差不齐，个别UTT人数多达百人，结构偏大;国家级UTT分布比较集中，“985工程”、“211工程”大学占79.17%，一般普通高校(特别是地方院校)几乎没有国家级UTT。为了更好地了解各团队综合实力情况及它们之间的差距，研究采用折中型模糊决策方法进行综合评价。

表1 广东省本科院校国家级教学团队基本情况(2007—2010)Tab.1 National teaching teams of Guangdong undergraduate colleges(2007—2010)

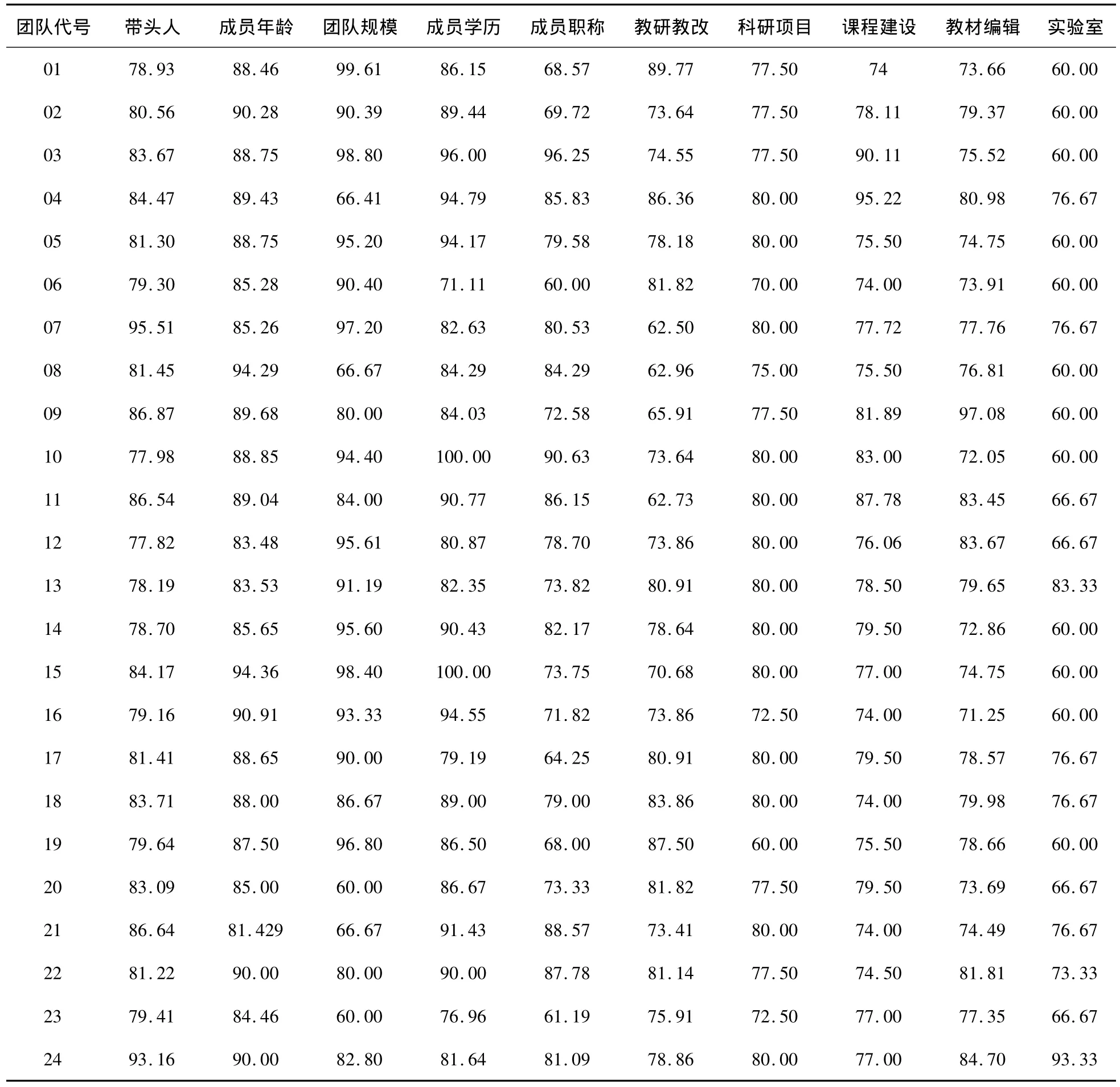
表2 广东省本科院校国家级教学团队(2007—2009)十项主要评价指标量化得分Tab.2 The evaluation of the state－level teaching team(2007 to 2009)ten quantitative scores of undergraduate institutions in Guangdong Province

2 折中型模糊决策

折中型模糊决策实际应用广泛，特别在经济［5］、军事［6，7］、电力［8］等多方案选优中表现优良。其基本原理［9］是从原始的样本数据出发，先对指标数据采用模糊三角数表达并进行归一化处理，然后找到模糊正理想值和模糊负理想值。对于正指标，模糊正理想值是每一个指标中模糊指标值的极大值，模糊负理想值是每一个指标中模糊值的极小值。然后，采用加权欧氏距离来计算各备选方案与模糊正理想值和负理想值之间的距离。在此基础上，计算各备选方案属于模糊正理想的隶属度，隶属度越大，方案越优。

设 Ω ={Ω1，Ω2，…，Ωm}为方案集，Ε ={Ε1，Ε2，…，Εn}为每一方案的指标集，α ={α1，α2，…，αn}为反映各指标相对重要程度的对应权重。模糊多属性决策是把已知的指标、权重大小和数据结构都相应的表示成决策空间中的模糊子集或模糊数，得到矩阵R=(rij)m×n。然后采用广义模糊合成算子对模糊权重向量α和模糊指标值矩阵R实施变换，得到H∶H=α⊗R，对于H中的元素采用模糊折中型决策方法对其进行排序，以此来对方案集Ω ={Ω1，Ω2，…，Ωm}进行综合评价。

折中型模糊决策评价的步骤如下:

第一步:指标数据的三角形模糊数表达

①对于定性指标，将两极比例法改进为三角模糊数比例法［8］，化定性指标为定量指标。

②对于定量指标，写成如下三角模糊数的形式:

a是定量指标值。

当所有的属性指标全部化为三角模糊数后，得到矩阵R=(rij)m×n。

③对于权重向量的三角模糊数表达，若权重是定量的形式给出的，则由式(1)可表示为

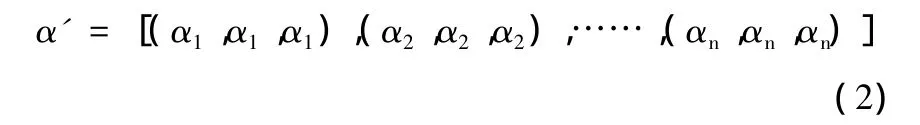
若权重是定性描述给出，则采用①的方法。

第二步:模糊指标矩阵H归一化处理

一般地，对m个评价方案的第j(j=1，2，…，n)个评价指标而言，在H中对应有m个模糊指标值，记为σi=(βi，γi，ηi)，(i=1，2，…，m)。将 σi进行归一化的具体公式如下:

①若σi是成本型指标对应的模糊指标值，则归一化公式为:

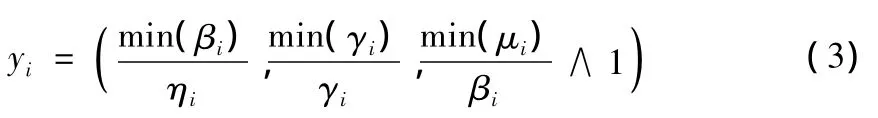
②若σi是收益型指标对应的模糊指标值，则归一化公式为:

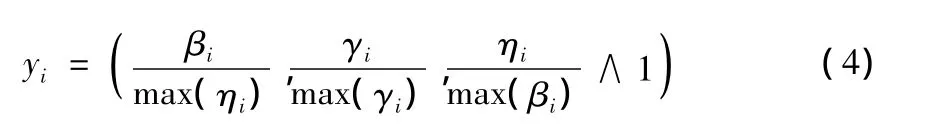
由此可得归一化后的模糊指标矩阵Π =(yij)m×n。

第三步:构造模糊决策矩阵

将归一化后的模糊指标矩阵Π进行加权处理可得到模糊决策矩阵 H=(πij)m×n，其中

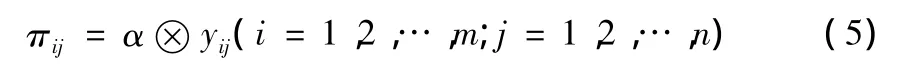
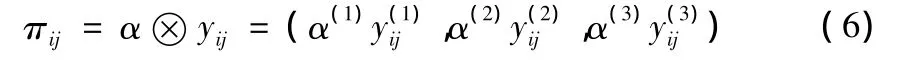
第四步:确定模糊正理想M+与模糊负理想M－

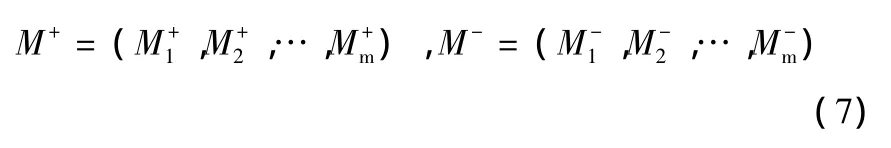
第五步:分别确定评价对象Ωi与模糊正、负理想M+、M－之间的距离

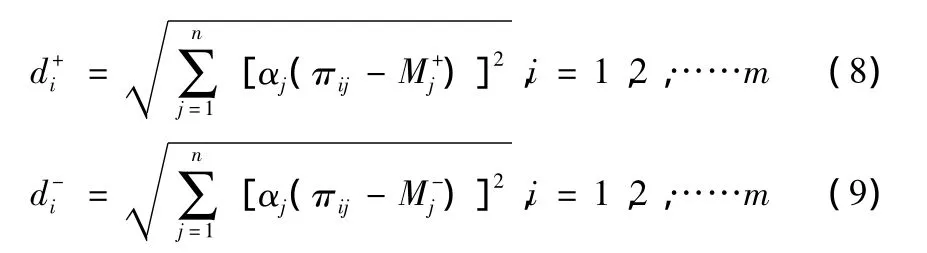
第六步:令评价对象Ωi以隶属度θi从属于模糊正理想，则:

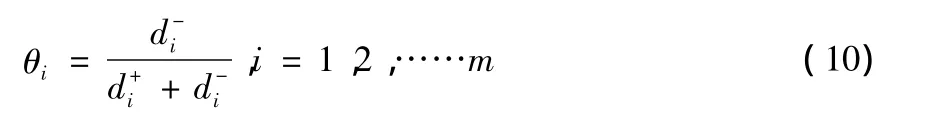
显然0≤θi≤1 ，若 Ωi与 M+越接近，则 θi越接近于 1。按隶属度 θi从大到小进行排序，θi越大，表示方案 Ωi越优。

3 广东省国家级教学团队综合评价

表2中给出了广东省本科院校国家级UTT 10项指标的量化数据，为了对这些UTT进行综合评价，本节采用折中型模糊决策方法。为了计算方便，对所给指标采用等额权重，即

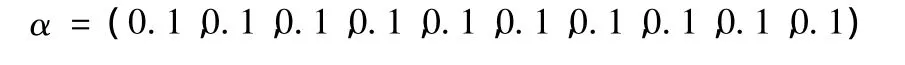
由于各指标已根据功效系数法进行量化，根据公式(1)把量化后的各团队指标、权重化成三角模糊数如下:

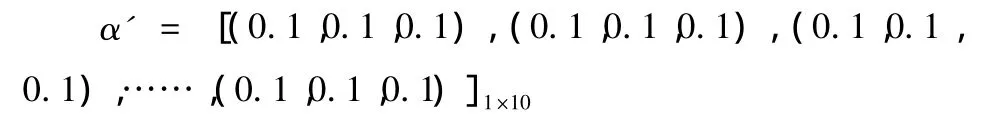
由公式(4)和公式(6)将数据进行归一加权化，根据公式(7)确定出模糊正理想值与模糊负理想值，由公式(8)～(10)进行模糊综合评价，计算结果如表3所示。

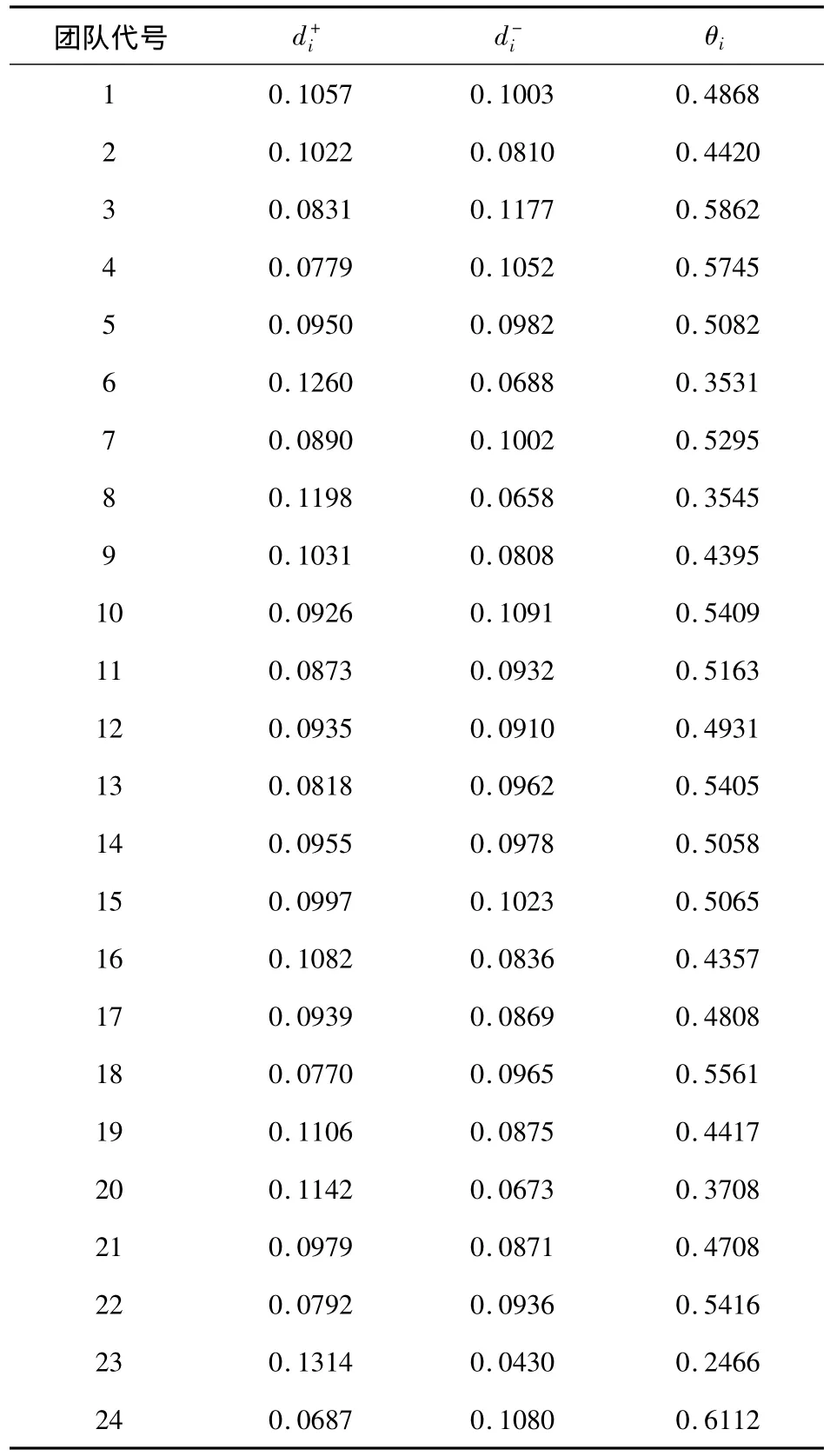
表3 广东省本科院校国家级UTT(2007—2009)折中型模糊综合评价计算结果Tab.3 Eclectic fuzzy comprehensive evaluation results of undergraduate institutions in Guangdong Province National UTT(2007—2009)

由表3可知，24个团队的综合实力水平的高低顺序依次为:

4 结论

从表2可见:(1)广东国家级UTT的年龄量化分值较高，说明其年龄层次较为合理，24支UTT中，30～49岁占74.67%，教师结构明显呈年轻化，中青年教师已成为质量建设工程中的中坚力量。(2)UTT的规模参差不齐，团队人数在13～24人时，其量化得分最高，为99.61～95.20分，而人数分别大于90人或小于6人时，量化得分最低，为66.41～60分，这说明UTT规模对团队建设有一定的影响，规模太大时，成员间信息传递环节繁缛，工作会相互推诿，从而相互信任和合作的矛盾将呈几何级数增长;规模太小时，则难以承担复杂多样的教学教改工作。因此，应适当控制UTT的规模，使其合理化。(3)24支UTT中，有10支拥有国家级或省级重点实验室，其实验室建设的量化分较高，但由于科类不同，部分UTT没有重点实验室，其分值为基本分，故此处评价亦有失衡之处。

研究在实际调研的基础上，挑选了评价本科院校教学团队的10项主要指标，采用折中型模糊决策方法，对广东省国家级UTT(2007—2009)进行了综合评价。从表3来看，团队从属于模糊正理想值的隶属度明显不均衡，表明各团队综合实力悬殊较大，差距明显;排名较前的团队大多分布在省内的名牌高校(如中山大学等)，这些UTT均表现出极强的教学教改能力、科研能力与资源优势。在综合排名处于前五位的UTT中，生化(含医学)团队有4个，文科团队1个，由此进一步表明优秀UTT的学科分布也不均衡。因此，广东省高校UTT建设应进一步整体规划，优化师资结构，整合教学资源，促进和谐发展，为提高省内高校教学质量的整体水平，逐步缩小省内高校教学与科研水平的差距，为推进质量工程和提高人才培养质量而努力。

［1］KARIN GOETZ.Perspectives on Team Teaching［EB/OL］.http://people.ucalgary.ca/～egallery/goetz.html，2012 －11 －15.

［2］刘宝存.建设高水平教学团队促进本科教学质量提高［J］.中国高等教育，2007，(5):29 －31.

［3］林晓新.UTT的类型、模式、结构、机制［J］.宁夏大学学报(人社会科学版)，2011，(5):163 －169.

［4］刘际陆.功效系数法在财务危机预测中的运用［J］.中国集体经济，2009，(4)上:84.

［5］李栋祥，张守凤，郑兆青.基于模糊折中型决策分析的多目标动态规划及其在投资决策中的应用［J］.山东理工大学学报(自然科学版)，2004，(1):19 －23.

［6］刘海涛，郭嗣琮.基于结构元理论的折中型决策方法［J］.辽宁工程技术大学学报(社会科学版)，2008，(1):52－55.

［7］杨云，任建军，王建华，等.模糊多属性决策在装备质量评价中的应用［J］.数学的实践与认识，2005，(3)，34 －38.

［8］张志毅，陈允平，袁荣湘.系统重构阶段机组最优恢复次序的模糊多属性决策法［J］.电工技术学报，2007，(11):153－157.

［9］刘焕彬，库在强，廖小勇，等.数学模型与实验［M］.北京:科学出版社，2008:178 －182.