基于蚁群算法的并行任务分配与调度
李艳生, 汪自云
(1.湖北师范学院 省级电工电子实验教学示范中心,湖北 黄石 435002;2.湖北师范学院 计算机科学与技术学院,湖北 黄石 435002)
0 引 言
现在正处于多核技术、网格计算、云计算的研究与发展阶段,其中任务的分配与调度是这些技术共同的核心问题。任务分配与调度是把一个计算任务分解成若干个彼此联系的子任务,使得这些子任务尽可能地并行执行, 从而使得所给定的计算任务能在最短的时间内完成。在通常的情况下,子任务的数量多于处理机的数量,在提高处理机的使用效率的同时使计算任务在尽可能短的时间内完成。高效的任务调度与分配是这些技术获取高性能的关键因素之一,研究任务分配与调度的最优化解对这些技术发展具有十分重大的意义。
任务分配与调度问题已经被证明是一个NP完全问题[1]。近年来出现一些用启发式算法(如模拟退火、遗传算法、蚁群算法)来解决NP完全问题,其中蚁群算法由于具有正反馈显示出解决NP完全问题的优势。用蚁群算法求解旅行商问题TSP(Traveling Salesman Problem)[2]、分配问题QAP(Quadratic Assignment Problem)[3]、调度问题JSP(Job-Shop Scheduling Problem)[4]等都取得较好的解。文[5]用蚁群算法求解n个任务分配到n个处理器的问题(一对一的关系)。文[6]用蚁群算法求解n个任务分配到m个处理器的问题(多对多的关系),但没有考虑到任务之间约束关系。文[7]用蚁群算法求解n个任务分配到m个处理器的问题(多对多的关系),虽然提到了任务之间的约束关系,但没有指出如何满足在约束关系条件下求解过程。针对如何在满足任务约束关系的条件下用蚁群算法求解任务分配与调度问题,本文首先对任务的分配与调度问题建立数学模型,然后在满足子任务之间的约束关系的条件下用蚁群算法求出最优解,最后把用蚁群算法与文[8][9]遗传算法的最优解进行对比。通过仿真实验表明,蚁群算法比遗传算法有较高的解的质量,但蚁群算法的求解速度要慢于遗传算法。
1 模型定义
1.1 问题模型
在并行计算中,任务分配与调度的数学模型可描述如下:一个计算任务T可分为n个子任务,由m个处理机进行处理。首先,假设每个子任务之间的依赖关系已知,一个任务依赖关系图通常是有向无回路图(DAG ),其 DAG图如图1所示。

图1 任务优先DAG图
图1中每个节点代表子任务,箭头代表前驱与后继的关系,即子任务Tj在它任一前驱子任务Ti完成之前而不能开始,其中T1是最早开始的子任务,Tn是最晚完成的子任务。
再次,假设每个子任务在m个节点的处理时间、节点之间的通信开销及有依赖关系的子任务之间的数据传输量已知。则异构计算中并行程序可抽象为一个五元组
F=(V,E,N,T,C)
(1)
其中:
V是任务优先DAG图中节点集合,子任务数为n个;
E是任务优先DAG 图中有向边Eij集合,边Eij(Vi,Vj) 表示子任务Vj要在子任务Vi完成之后才能开始;
N是异构环境中可用的处理节点集合,处理机数为m个;
T是每个子任务执行时间开销集合,Tik表示子任务Ti在处理机Nk上的执行时间;
C是任务优先DAG图有向边的通信开销集合,Cij表示子任务Vi与Vj通过有向边Eij的通信成本,当Vi和Vj分配在同一处理机上Cij=0时 。
要达到的目标是, 在满足任务处理时序和资源限制的条件下寻找一种合理的分配与调度策略, 将n个子任务指派到m个处理机上, 合理调度各个子任务的执行顺序, 使得各个任务在满足依赖关系图的约束下, 整个大任务的完成时间最短。
假设S为某个DAG 图的一个分配与调度方案,Ts(Nk)表示在分配与调度S下,当处理机Nk完成所有指派到本处理机上子任务所要花费的总时间。设T(S)表示整个分配与调度S所要花费的总时间,则有T(S)=∀k(Max(Ts(Nk))),(0≤k≤m-1).分配与调度的目标就是寻找T(S) 最小的分配与调度方案S,即∀S(Min(T(S))) .
1.2 解模型
本文采用一种排列方法[8]来表示DAG任务图的分配与调度的解,每个处理机上所有任务排成一个列表, 排列的顺序代表了各个子任务的先后执行顺序。对DAG的一个分配调度S,记S=(L0,L1,L2,…,Lm-1)其中Li=(Ti0,Ti1,Ti2,…,Ti(k-1))分别表示分配到处理机Ni上的k个子任务序列。
为了证明编码的合法性,引入DAG 图高度值H(Ti) :
(2)
其中Pre(Ti)表示Ti的前驱集合,Φ表示空集。根据高度值H(Ti) , 称一个调度是合法分配与调度, 是指该调度中所有列表的任务是按高度值的升序排列的,即H(Ti0≤H(Ti1≤…≤H(Tik).
2 算法设计
2.1 基本原理
蚁群算法是由Dorigo M.教授在1991年首先提出的,其基本思想是蚂蚁个体之间通过一种称之为信息素的物质进行信息交互, 从而能相互协作, 完成最短路径的寻址。蚂蚁会在走过路径上分泌信息素,路径越短,单位时间里经过此路径的蚂蚁越多,分泌的信息素也会越多,就会吸引更多的蚂蚁选择此路径,从而找出最短路径。因此,由大量蚂蚁组成的蚁群的集体行为便表现出一种信息正反馈现象:某一路径上走过的蚂蚁越多,则后来者选择该路径的概率就越大。
设有n个子任务,m个处理器,l只蚂蚁,则第k只蚂蚁把子任务i分配到处理器j的概率:
(3)
其中τ(i,j) 表示蚂蚁k把子任务i分配到处理器j时产生的信息素,η(i,j)表示启发式信息,α(0≤α≤1),β(0≤β≤1) 体现信息素和启发式信息对蚂蚁选路的权重,Ak(i)表示蚂蚁k分配子任务i时可以选择的处理器集合,向处理器分配任务的原则是每个处理器达到平均负载时就不能再分配其它任务。
(4)
其中T(i,j)表示子任务i在处理器j上执行时间。
τ(i,j)=(1-ρ)*τ(i,j)+△τ(i,j)
(5)
(6)
其中ρ(0<ρ<1) 表示信息素的挥发系数,τ(i,j)初始化值为处理器平均执行时间的倒数,△τk(i,j) 表示蚂蚁k在一次循环中把子任务i分配到合法的处理器j时产生的信息素, △τ(i,j)表示所有蚂蚁在一次循环中把子任务i分配到合法的处理器j时产生的信息素。
(7)
其中Q是常数,Zk表示蚂蚁k在本次循环中路径长度。
2.2 算法实现
要使解满足子任务间的约束关系,则分配到各个处理器的子任务列表应按DAG高度值H升序排列。首先把子任务按DAG高度值H升序排列一个表,蚂蚁在寻路时按表顺序把每个子任务分配到处理器,这样的解即是合法解。初次循环时蚂蚁系统随机地把子任务 分配到合法的处理器j,然后蚂蚁根据(3)把子任务i分配到合法的处理器j.每只蚂蚁经过n步循环一次产生一个合法解。其具体算法描述如下:
1)读入任务优先DAG 图,并根据公式(2)计算每个节点的高度值H;
2)设置常数α,β,ρ,Q,Nc,其中Nc表示循环次数;
3)根据DAG图把n个子任务按高度值H的升序排成一个表;
4)根据公式(4)设置启发式信息η和初始化信息素τ;
5)判断循环次数否已达到Nc或多次循环解无变化,如果是,转14,否则转6继续;
6)把m个处理器加入Ak(i)集合;
7)判断本次循环蚂蚁k是否已经过了n步,如果是,转13,否则转8;
8)根据处理器负载设置Ak(i) 集合;
9)判断是否是第一次循环,如果是,转10,否则转11;
10)蚂蚁k随机地把子任务i分配到合法的处理器j;
11)根据公式(3)计算pk(i,j) ,再根据pk(i,j)选择处理器j;
12)根据公式(5)(6)(7)更新信息素 ;
13)判断是否所有蚂蚁都到达终点,如果是,转5进入下一次循环,否则转6处理下一只蚂蚁;
14)输出最优化解。
3 实验分析
根据建立的模型和设计的蚁群算法,进行相应的仿真实验。软件开发环境采用Java6开发,硬件运行环境为P3 866MHz/192MB.实验参数设置如下:α=0.8,β=0.2,ρ=0.01,Q=200,Nc=100,蚂蚁数量l为100只。DAG 图随机生成的,每个结点有1~ 4个后继,估计运行时间为1~ 20间的随机数, 各处理机间数据传输延时也是随机生成的。其实验数据如表1所示。
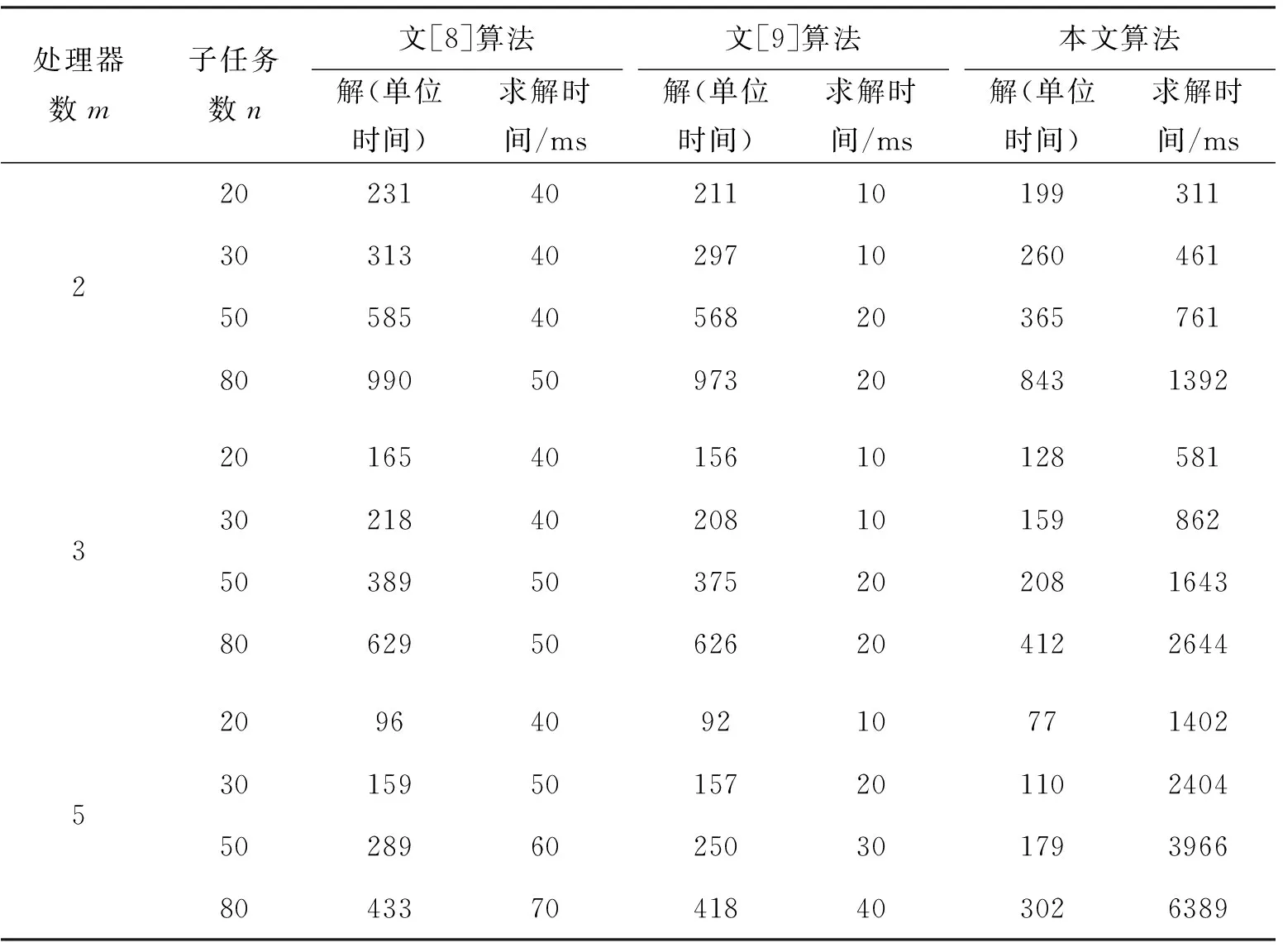
表1 几种算法的实验结果
从表1实验结果可以看出,本文用蚁群算法求出的任务分配与调度最优化解的质量远高于遗传算法,但蚁群算法求解速度慢于遗传算法。可见蚁群算法在求解NP完全问题中具有较大的优势,但求解速度有待改进。
4 结 语
蚁群算法虽然出现的时间并不长,用蚁群算法解决NP完全问题在解的质量方面具有明显优势。但尚需解决所存在的求解速度慢问题,如果考虑引入分布蚁群寻径策略(多蚁群寻径),在面向一类NP完全问题求解过程实现多算法协同,将有待进一步研究。
[1]Correa R C, FerreiraA, Rebreyend P. Scheduling Multiprocessor Tasks with Genetic Algorithms[J]. IEEE Transactions on Parallel and Distributed Systems, 1999, 10(8): 825~837.
[2]Dorigo M,Gambardella L M.Ant colony system:a cooperative learning approach to the traveling salesman problem[J].IEEE Transactionson Evolutionary Computation,1997,1(1):53~66.
[3]Gambardella L M,Taillard E,Dorigo M.Ant colonies for the quadratic assignment problem[J].Journal of the Operational Research Society, 1999,50:167~176.
[4]Colorni A,Dorigo M,Maniezzo V.Ant system for job-shop scheduling[J].Belgian Journal of Operations Research,Statistics and ComputerScience,1994,34(1):39~54.
[5]杨 冬,王正欧. 改进的蚂蚁算法求解任务分配问题[J]. 天津大学学报, 2004, 37(4): 373~276.
[6]王灵霞,张远平,吴佩莉.蚁群算法求解分布式系统任务分配问题[J].计算机工程与设计, 2008,29(6):1472~1474.
[7]张 勇,张曦煌.改进型蚁群算法的多处理机任务调度研究[J].计算机工程与应用,2007,43(35):75:76.
[8]Edwin S H,Hou N An sari.Genetic Algorithm for Multiprocessor Scheduling[J]. IEEE Trans on Parallel and Distributed Systems,1994,5(2):113~120.
[9]钟求喜, 谢 涛, 陈火旺. 基于遗传算法的任务分配与调度[J].计算机研究与发展,2000, 37(10): 1197~1203.

