基于SIMP 理论的电动汽车车身多目标拓扑优化

谢伦杰，张维刚，常伟波，崔 杰

(湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082)

前言

拓扑优化是一种根据约束、载荷和优化目标而寻求材料最佳分配的优化方法，主要应用在产品开发的概念设计阶段。拓扑优化在设计初始阶段即被引入，可优化空间大，对最终产品的成本和性能有非常重要的影响［1］。电动汽车能有效解决能源短缺和环境污染问题，已成为汽车行业的研究热点。由于驱动、储能装置的特殊性，传统的车身结构难以满足电动汽车的性能要求［2］;电动汽车主要通过柔性的电线传递能量，其各部件的布置具有很大的灵活性，这为拓扑优化创造了有利的条件。

目前电动汽车车身的拓扑优化主要集中在单目标的优化分析［3-5］，但车身结构作为承载基体，须满足多种静态工况和动态工况下的性能要求，是一个多目标拓扑优化问题［6］。为了同时满足电动汽车车身多种静态载荷工况和动态频率特性的要求，本文中以平均柔度最小和平均频率最大为总目标，对电动汽车车身实现多目标拓扑优化，得到较为清晰的承载结构，避免了单目标拓扑优化无法同时考虑其他因素的缺点。

1 拓扑优化数学模型及算法

1.1 SIMP插值模型

拓扑优化是一个“0-1”问题，即结构件材料的“有”与“无”的问题。由于不可能把设计区域中的每个点都作为一个设计变量，故必须对设计区域进行离散，但离散问题在数学上很难处理，通常将此问题转化为连续问题去研究，变密度法就是这一思路的产物［7］，其基本思想是人为引入一种假想的密度可变材料，优化时以材料密度为设计变量，将结构拓扑优化问题转换为材料的最优分布问题。

文献［8］中对密度法材料插值模型进行研究，提出一种基于正交各向同性材料密度幂指数形式的带惩罚的实体各向同性材料(solid isotropic material with punishment，SIPM)，即变密度法材料密度插值理论。优化时以单元设计变量的大小决定单元取舍，采用惩罚因子约束抑制介于0～1之间的单元，使中间密度值尽量向0与1两端聚集，使连续变量的拓扑优化模型能很好地逼近0-1离散变量的优化模型。SIMP材料插值模型假设材料的弹性张量各向同性，泊松比为与密度无关的常量，材料属性随着单元相对密度的变化而变化，其具体关系式［9］为

式中:E0和E(ρ)为初始和优化后弹性模量;K0和K(ρ)为初始和优化后刚度矩阵;P为惩罚因子，P＞1;ρ为材料密度;ρmin为材料为空的最小密度值。

1.2 拓扑优化数学模型

1.2.1 静态拓扑优化数学模型

静态单工况下，以结构单元的相对密度作为设计变量，以体积分数作为约束条件，以结构柔度的最小化(即刚度最大化)作为目标函数，建立基于SIMP理论的连续体结构拓扑优化数学模型:

式中:ρi为结构单元的相对密度;C为结构的总体柔度;U为位移矩阵;P为惩罚因子;K为优化前的结构总刚度矩阵;F为力列向量;ui为单元位移列向量;k0为结构初始单元刚度矩阵;V为优化后的结构总体积;V0为初始结构总体积;α为体积分数;vi为优化后的单元体积;ρmin为设计变量的下限，其目的是防止单元刚度矩阵奇异。

多工况情况下，不同的载荷工况将得到不同的拓扑结构。传统的多工况优化问题采用线性加权叠加法将多目标问题转化为单目标问题求解，但对于非凸优化问题来说，该方法不能确保得到的所有帕累托(pareto)解为最优解［10］，故采用折衷规划法结合功效函数法来解决此问题。折衷规划法的基本思想是把多个子目标函数正规化，并给每个子目标加权后合成一个单目标。功效函数法是根据多目标规划原理，对每一项子目标确定一个理想值和不允许值，以理想值为上限，不允许值为下限，再经过加权平均进行综合，从而评价被研究对象的综合状况［11］。由折衷规划法结合功效函数法得到静态多工况下拓扑优化的目标函数:

式中:m为载荷工况总数;wk为第k个工况的权值;P为惩罚因子(P≥2);Ck(ρ)为第k个工况的柔度目标函数、分别为第k个工况柔度目标函数的最大值和最小值。

1.2.2 动态拓扑优化数学模型

动态拓扑优化是为了改善结构的模态特性。如果将某一阶频率的最大化作为目标函数，在优化迭代过程中，由于结构材料的删除等修改，当一个阶次的频率达到最大时，其他阶次的频率可能降到一个较低的值，几阶频率之间可能相互调换次序，发生模态交换现象，从而引起振荡并干扰模型求解收敛，使优化设计的收敛性和稳定性得不到保证。为了克服这种现象，采用平均频率公式［12］来定义优化的目标函数，建立动态频率拓扑优化数学模型:

式中:Λ(ρ)为平均频率;λj为第 j阶特征频率;λ0、s为给定的参数，用来调整目标函数;wj为第j阶频率的权值系数;f为需要优化的低阶频率的阶次;M为总质量矩阵;φj是第j阶振型向量。

1.2.3 静态-动态联合拓扑优化数学模型

为了使优化结果具有良好的静态特性和动态特性，同时考虑静态刚度目标和动态振动频率目标为拓扑优化的总目标函数。由于两者的数量级存在较大的差异，计算时容易忽略小数量级目标函数在优化中的作用，使计算结果受到数量级高的目标函数的支配。为了平衡两者数量级之间的差异，目标函数先经如下形式的归一化定义:

式中:fi(x)为第i个目标函数;wi为第i个目标函数的权系数;x为设计变量;si为标度因子，使每个目标函数有相同数量级，并在优化中占有同等地位。

建立静态-动态联合拓扑优化数学模型如下:

式中:F(ρ)为静动态联合总目标函数;w为柔度目标函数的权重;Λmin、Λmax分别为频率目标函数的最小值和最大值，用来消除量纲。

1.3 拓扑优化求解算法

连续体结构拓扑优化的求解算法主要有优化准则法和数学规划法。其中数学归纳法求解结构优化问题时，通常需要计算目标函数、约束函数和它们的导数，计算效率较低。优化准则法是一种间接优化方法，不直接优化目标函数，而是把数学中最优解应满足的库恩塔克(Kuhn-Tucker)条件作为最优结构应满足的准则来更新设计变量和拉格朗日乘子，收敛速度快，迭代次数少且与结构大小和复杂程度无关，尤其对体积约束下的最小柔度问题的求解更为有效［13］，因此采用优化准则法求解并构造拉格朗日(Lagrange)函数:

式中:η1、η2、η3、η4为拉格朗日乘子，η1为标量，η2、η3、η4为向量;ρ 是 ρi组成的向量;ai、bi为松驰因子。由此可得库恩塔克条件和设计变量迭代公式:

1.4 拓扑优化流程

利用Hypermesh软件的Optistruct模块进行拓扑优化的流程如图1所示。

2 电动汽车车身拓扑优化

2.1 载荷工况分析

依据电动汽车的使用情况和实际载荷工况，选择以下4种典型工况作为模型分析载荷工况。

(1)弯曲工况 弯曲工况模拟电动汽车四轮着地、匀速直线行驶。考虑满载情况，车上共有4名乘员，每位乘员体质量为65kg，行李总质量为40kg。约束左前轮全部自由度和其余3轮z方向上的平动自由度。

(2)扭转工况 扭转工况模拟各车轮悬空状态，分别释放对应悬空车轮的全部自由度，同时在悬空一端的车轴上施加一极限转矩(车轴负荷的一半乘以轮距)，约束悬空同轴对称车轮除x方向平动自由度以外的全部自由度和其他两轮的全部自由度。

(3)紧急制动工况 紧急制动工况主要考虑电动汽车以最大减速度制动时，地面制动力对车身的影响。在x方向上附加-0.8g的惯性力。约束前轮的全部自由度和后轮除x方向平动自由度外的全部自由度。

(4)急转弯工况 主要考虑当电动汽车以最大转向速度转弯时，惯性力对车身的影响。在y方向附加0.4g的离心力。释放一侧车轮y方向的平动自由度，约束另一侧车轮的全部自由度。

2.2 拓扑优化计算

根据电动汽车的结构布置特点，扣除乘员舱、行李舱、动力总成、轮胎包络和风窗玻璃等所占据的部分，确定剩余部分为优化设计空间如图2所示。在Hypermesh软件中采用六面体单元划分网格，定义材料属性，确定载荷和边界条件，建立拓扑优化有限元模型。

多目标拓扑优化的函数公式在OptiStruct软件中不能直接调用，因此借助于软件中的用户自定义方程功能来实现。先定义静态折衷规划公式和动态平均频率公式，然后把定义好的函数设为响应，最后把该响应作为目标函数进行拓扑优化。

在进行单目标拓扑优化时发现，以刚度作为目标函数进行优化时，平均柔度达到最优，但平均特征值却很小;而以频率作为目标函数进行优化时，平均特征值达到最优，但平均柔度却很大。这表明静态刚度和动态频率是两个相互矛盾的目标函数，权重分配相差过大时难以使刚度和频率目标函数同时达到最优，而车身结构作为各个部件的承载基体，首先应保证其刚度要求，出于这样的考虑，取柔度目标函数的权值为0.6，频率目标函数的权值为0.4。

以优化设计空间内每个单元的相对密度为设计变量，以体积分数为约束，以自定义的静动态联合总函数公式为目标函数，在OptiStruct软件中建立拓扑优化计算模型。由于约束条件对最终的拓扑优化结果影响较大，因此先分别选取体积分数α为0.2和0.4的约束条件进行拓扑优化试计算，假定单元相对密度在0.15以下的区域为无材料分布，优化结果如图3所示。

从试算结果可以看出，约束为α=0.2时，删除材料单元过多，约束为α=0.4时，保留材料单元过多，均不是最佳的材料布局方式。选取约束为α=0.3进行拓扑优化计算，求解拉格朗日乘子，采用优化准则算法计算迭代因子，更新设计变量。经过30步迭代计算，没有发生振荡现象，目标函数趋于收敛，其收敛曲线如图4所示，拓扑优化结果如图5所示。通过对优化结果观察可以发现清晰的载荷路径，图6为截取前舱部分的载荷路径。

拓扑优化计算结果对车身结构的载荷传递路径和材料布局方式具有指导意义，但与工程实际仍有较大的距离，根据实际情况和经验资料进行适当的修正后初步确定电动汽车车身结构如图7所示。

3 拓扑优化结果分析

由于所研究对象为微型电动汽车，根据厂家的设计用途，该电动汽车主要作为城市代步工具使用，最高行驶速度的设计要低于传统燃油汽车，使用环境和极限工况也优于传统燃油汽车，因而其车身的设计要求也相应地低于同类型的传统燃油汽车。依据拓扑优化分析结果，建立相应的有限元模型，对其静动态结构特性进行分析，验证优化设计方案的可行性。有限元静态分析结果如表1所示。从表1中可以发现，各载荷工况的应力最大值均在材料应力的许可值范围内，其中最大应力为141.1MPa，最大变形为7.6mm，出现在扭转工况的后悬支撑与车架连接区域;其余各工况下最大应力均小于100MPa，最大变形为2～3mm，车身结构基本满足静态刚度设计要求。在下一步的详细设计中，扭转工况下的车身结构刚度可以做进一步的优化改进。

表1 有限元静态分析结果

由于低频振动比高频振动危险，前几阶振动对结构的动态性能影响较大，故模态分析中只选取前5阶的模态振型进行分析，结果如表2所示。由于电动汽车的驱动装置采用平衡性更好的电机代替传统的发动机，有效减少了整车的振动激励;而路面激励随道路条件决定，高速公路和城市较好路面的激励多在3Hz以下，因而只须重点校验车身结构的低阶频率是否高于非簧载结构的固有频率(一般为6～15Hz)。由表中数据可以看出，前3阶的振动频率为24.4～54.5Hz，有效地避开了路面对汽车的激励频率范围，且高于非簧载质量的固有频率，避免了共振的产生。从频率分布上看，1阶扭转振型频率为24.4Hz，1阶弯曲振型频率为36.2Hz，车身整体弯曲刚度大于扭转刚度，两种固有频率明显错开，主要的弯扭模态没有耦合。

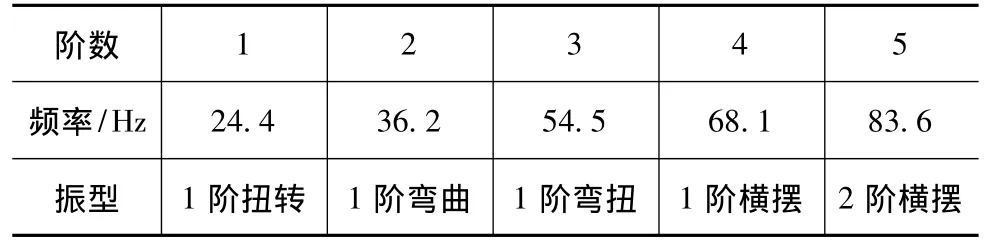
表2 有限元动态分析结果

4 结论

对电动汽车车身结构静动态多目标拓扑优化方法进行探讨。基于SIMP材料插值理论，在对目标函数进行归一化以消除数量级差异后，以平均柔度最小和平均频率最大为总目标，利用优化准则法建立设计变量的迭代方程，同时考虑约束条件对优化结果的影响，选取不同的体积分数对电动汽车车身结构进行拓扑优化，得到车体结构清晰、载荷路径明显的优化结果。有限元分析结果表明，采用此方法设计的车身结构具有较好的静动态特性，满足设计要求。该方法为电动汽车车身各部件的下一步详细设计和其它车型的车身开发提供思路和参考依据。

［1］Bendsoe M P，Sigmund O.Topology Optimization:Theory，Methods and Applications［M］.Berlin:Springer，2003.

［2］谢庆喜，张维刚，钟志华.电动汽车电池架的耐撞性仿真设计与优化［J］.汽车科技，2005，5(3):25-28.

［3］高云凯，姜欣，张荣荣.电动改装轿车车身结构优化设计分析［J］.汽车工程，2005，27(1):115-117.

［4］丁利.结构拓扑优化分析在电动小车车身的轻量化的应用［J］.中国制造业信息化，2009，38(11):58-60.

［5］徐晓瑜，郭永进.电动低速汽车车身结构刚度约束拓扑优化设计［J］.机械设计与研究，2010，26(2):110-113.

［6］Chen T Y，Wu S C.Multi-objective Optimal Topology Design of Structures［J］.Computational Mechanics，1999，17(4):269-278.

［7］范文杰，范子杰，桂良进，等.多工况下客车车架结构多刚度拓扑优化设计研究［J］.汽车工程，2008，30(6):531-533.

［8］Bendsoe M P，Sigmund O.Material Interpolation Schemes in Topology Optimization［J］.Arch Appl Mech，1999，69:635-654.

［9］左孔天，陈立平，钟糗芳，等.基于人工材料密度的新型拓扑优化理论和算法研究［J］.机械工程学报，2004，40(12):31-37.

［10］Min S，Nishiwaki S，Kikuchi N.Unified Topology Design of Static and Vibrating Structures Using Multi-objective Optimization［J］.Computers and Structures，2000，75:93-116.

［11］Marler R T，Arora J S.Survey of Multi-objective Optimization Methods for Engineering［J］.Struct Multidisc Optim，2004，26:369-395.

［12］Ma Z D，Kikuchi N.Topological Design for Vibrating Structures［J］.Comput.Methods Appl.Mech.Engrg，1995，121:259-280.

［13］孙靖民.机械优化设计［M］.北京:机械工业出版社，2005:167-172.