矩孔夫琅禾费衍射图样的仿真研究

谭 毅

(陕西理工学院物理与电信工程学院，陕西汉中723003)

0 引言

光的衍射是指光波在其传播路径上如果遇到障碍物，它能绕过障碍物的边缘偏离直线传播而进入几何阴影区，并在屏幕上出现光强不均匀分布的现象，反映了光的波动特性，而夫琅禾费衍射既能反映出衍射的一些基本特征，又具有特殊的简单性。

通常在夫琅禾费衍射中改变孔的形状［1-13］，衍射光斑形状会发生明显的变化。本文根据惠更斯-菲涅尔原理，应用Matlab软件编程，模拟了矩孔夫琅禾费衍射的图样分布，通过改变方孔的尺寸、矩孔的边长以及棱形小孔的形状等参数，观察到矩孔衍射图样的相应变化。通过对光的衍射现象的研究，可以深入、具体地了解光的波动性，有助于学生更加深刻地理解矩孔夫琅禾费衍射的特征和规律，提高教学质量。

1 夫琅禾费矩孔衍射的光强分布

假设矩形孔沿x、y方向的边长分别为m、n，衍射光波的方向用二维衍射角α、β表示，在近轴条件下，即 sin α≈tanα =x/f，sinβ≈tan β=y/f，则衍射光波在透镜焦平面上点Q(x，y)的相对强度为［14］

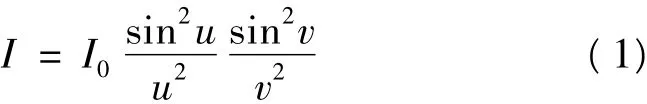
式中:I0为屏幕中央点的光强，即为最大光强;

f为透镜的焦距。由式(1)可以看出，矩形孔衍射的相对强度是2个单缝衍射因子的乘积，若mn，矩形孔就变成了平行于x轴的狭缝，夫琅禾费衍射图样将集中在y轴上，衍射光仅沿垂直于狭缝方向扩展，此时变成单缝夫琅禾费衍射，只需进行一维计算，则此时Q点强度分布为(在傍轴近似条件下)

若将方孔转过45°，则变成棱形，调节棱形两条对角线的长度，则可以得到不同的衍射图样，衍射屏上任意点Q的强度分布为(在傍轴近似条件下)［15］

2 仿真研究

设入射波长λ=632.8 nm，焦距f=50 mm，孔的边长为 m=0.01 mm，n=0.01 mm，逐一改变上述参数可以得到矩孔衍射图样的变化情况。

2.1 方孔大小变化对衍射图样的影响

改变方孔的边长可以得到不同衍射图样，如图1所示，图右侧的曲线是分别从图中取x=0的衍射光强分布，并进行归一化。从图中可以看出，随着方孔边长的增加，条纹变窄、变密。其原因由式(1)可知，由于方孔边长的增加，相同各级次的衍射角变小，能观察到的衍射级次增加;从衍射强度曲线也可以看出，随着方孔边长的增加，其中央明纹的宽度在减小，衍射效果也逐渐的不明显。

图1 方孔大小变化对衍射条纹分布的影响

2.2 矩孔宽度变化对衍射图样的影响

取矩孔的长度m=0.01 mm，改变矩孔的宽度n，可以得到不同衍射图样，如图2所示，图右侧的曲线是分别从图中取x=0 mm的衍射光强分布，并进行归一化。从图中可以看出，随着矩孔宽度的减小，x轴方向能显示的条纹级数和位置虽然没有变化，但逐渐被拉长了，y轴方向能显示的条纹级数在减少，即衍射效果逐渐明显，最后变成了单缝衍射图样，如图2(c)所示。其原因由式(2)可知，由于mn;从衍射强度曲线也可以看出，随着矩孔宽度的减少，其中央明纹的宽度在增加，衍射效果也逐渐的明显。

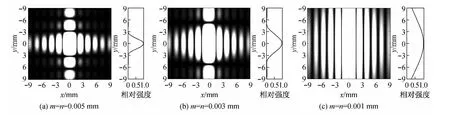
图2 矩孔宽度n变化对衍射图样的影响

2.3 棱形小孔的形状变化对衍射图样的影响

改变棱形小孔对角线的长度比，可以得到不同衍射图样，如图3所示，其对角线的长度比分别为4∶4、4∶3和4∶2，图右侧的曲线是分别从图中取x=0 mm的衍射光强分布，并进行归一化。从图中可以看出，随着棱形小孔高度对角线的长度减小，条纹变宽、变疏，其原因由式(1)可知，由于棱形小孔变小的增加，相同各级次的衍射角变大，能观察到的衍射级次减少;从衍射强度曲线也可以看出，随着棱形小孔高度对角线的长度减小，其中央明纹的宽度在增加，衍射效果也逐渐的明显。

图3 棱形小孔的形状变化对衍射图样的影响

3 结语

本文根据惠更斯-菲涅尔原理，应用Matlab软件编程，模拟了矩孔夫琅禾费衍射的图样分布，通过改变方孔的尺寸、矩孔的边长以及棱形小孔的形状等参数，观察到矩孔衍射图样的相应变化。这种计算机仿真方法扩展了矩孔衍射问题的研究途径与方法，具有一定的应用价值，尤其对于教学具有直观作用。

［1］ 成泰民，曹连刚.不同三角形孔的Fraunhofer衍射图样模拟［J］.广西物理，2011，31(1):33-36.

［2］ 王丽芝，成泰民，葛崇员，等.不同四边形孔的Fraunhofer衍射图样模拟［J］.沈阳理工大学学报，2010，29(6):88-91.

［3］ 葛崇员，成泰民，孙树生.不同矩形孔的Fraunhofer衍射图样模拟［J］.沈阳师范大学学报，2010，28(3):371-373.

［4］ 陆朝华，蓝海江.日光夫琅禾费双矩孔衍射的计算机仿真［J］.安徽农业科学，2012，40(5):2966-2967.

［5］ 杨 坤，成泰民，葛崇员.矩形孔和圆孔构成的双孔Fraunhofer衍射图样模拟［J］.沈阳师范大学学报，2012，30(1):36-39.

［6］ 刘东州，侯志青，刘立芳.方孔夫琅禾费衍射的数值模拟［J］.大学物理，2011，30(4):38-42.

［7］ 章志敏，戴建明，夏明荣，等.微波矩孔衍射仿真与实验［J］.大学物理实验，2010，23(1):43-45.

［8］ 常 山，桑志文，高志强.单色点源矩孔衍射的模拟与分析［J］.光学仪器，2009，31(2):68-71.

［9］ 王永祥.矩孔菲涅耳衍射的光强分布［J］.量子电子学报，2010，27(3):264-269.

［10］ 王丽芝，成泰民，祁 烁.对称六边形孔的Fraunhofer衍射图样模拟［J］.佳木斯大学学报，2011，29(1):135-138.

［11］ 李 多，景红梅，平 澄，等.六角孔的夫琅禾费衍射场的实验演示［J］.物理实验，2010，30(6):5-7.

［12］ 周 峰，徐代升.任一衍射屏的构建及其夫琅禾费衍射仿真［J］.江西科学，2011，29(5):555-559.

［13］ 汪 峰，傅洪波，赵箭光.任意形状孔夫琅禾费衍射的计算机模拟［J］.软件导报，2010，9(12):190-191.

［14］ 张志峰，苏玉玲，蒋逢春，等.基于MATLAB的夫琅和费衍射实验的计算机仿真［J］.电脑与电信，2011(6):26-27.

［15］ 戴又善.二维小孔的对称变换与夫琅禾费衍射光强分布［J］.大学物理，2011，30(11):22-27.