一种基于Delaunay剖分三角形内插值的摄像机标定方法
徐 侃,李文龙,尹周平
(华中科技大学 数字制造装备与技术国家重点实验室,湖北 武汉 430074)
视觉定位因其具有非接触、高精度、高速度等特点,在RFID标签封装机、装片机、划片机、引线键合机电子封装设备上得到广泛应用[1~2]。摄像机标定是视觉定位的重要环节之一,用于校正图像采集、传输及处理过程中引入的变形,并建立由图像坐标到世界坐标的转换关系[3]。目前摄像机标定方法大多基于三维测量原理,从不同位置拍摄的多幅标定图像计算摄像机内、外参数[4~5]。电子封装设备标定对象为平面距离和角度,要求尽可能减少人工干预,提升在线运行效率。因此,开发操作方便、计算复杂度小且精度满足电子封装设备运行需要的标定算法,具有重要的理论意义和实用价值。
针对在线摄像机标定中减少人工干预的需求,国内外研究者提出一种基于多项式拟合的摄像机标定方法[6~7]。该方法基于小孔成像模型,将常见图像变形(平移、旋转、非线性畸变)的数学模型,以一个二元五次多项式表示。通过带入变形前后特征点的像素坐标拟合计算得到上述多项式的系数,从而完成标定计算。该方法只用一幅图像即可完成电子封装设备所需的标定计算且精度满足要求,因此,得到了普遍应用。但该方法的计算过程涉及到了高阶(21阶)矩阵的求逆运算,计算复杂度较高且易出现奇异情况(矩阵的逆不存在)。
本文提出一种基于Delaunay剖分三角形内插值的摄像机标定方法,简称CIDT(Calibration based on the Interpolation ofDelaunay Triangles)方法。该方法利用了特征点网格Delaunay剖分三角形的性质以及有效剖分三角形区域的内插值线性关系不变性,使用计算复杂度更低的三角形内插值算法取代原有的多项式拟合算法。在不降低标定精度的前提下,简化了标定计算,降低了标定算法实现的难度。
1 标定特征点信息提取
1.1 特征点图像坐标的提取
目前,常用的标定板靶标有棋盘格型与圆点阵列型。棋盘格型靶标采用棋盘格四周的角点作为特征点,这类靶标制作简单、适用性广泛。对于这类靶标特征点的提取,可以采用基于灰度值相关的Harris角点检测算法,通过求取特定区域的梯度相对于相邻区域的梯度均值的变化规律以及相邻区域之间梯度分布的相关性来求取CIM (Cornersof Image Marking)[8],最后根据CIM中大于指定阈值的局部极大值来确定角点[9]。
圆点阵列型靶标采用圆形区域中心作为特征点,具有更高的标定精度,在IC封装设备上被广泛应用。对于这类靶标特征点的提取,可以采用区域轮廓椭圆拟合算法,通过提取特征点区域的轮廓点以椭圆方程作为目标式进行最小二乘拟合得到其对应的椭圆方程,方程对应的椭圆中心即为该特征点区域对应的中心坐标[10]。
1.2 特征点网格坐标的计算
CIDT方法对标定靶标的成像有如下三个要求:第一,特征点尽可能地充满整个图像且特征点网格中每一行的点个数相等;第二,特征点网格中每一行特征点的图像行坐标范围与其它行没有交集;第三,用户应输入特征点网格的行数R 以及列数C。
在满足上述要求的前提下,假设特征点集P 中每个特征点Pi(i 为特征点坐标提取时的顺序序号)的像素坐标为(xi,yi),按照如下步骤完成P 中每个特征点像素坐标与记录了其在特征点网格上所处位置的网格坐标之间的对应:
步骤1:根据像素坐标(x,y)中的行坐标y 对P 中的所有特征点按照从小到大的顺序排序,得到的排序后特征点集记作P'。
步骤2:将P'中的特征点分为R个小组,每个小组C个点。在每个小组内根据像素坐标(x,y)中的列坐标x 对组内的特征点按照从小到大的顺序排序,得到的再次排序后特征点集记作P"。
步骤3:对特征点集P"中的每个特征点Pj(j 为经过两次排序后的特征点顺序序号),按照式(1)计算得到其网格坐标(rj,cj)。其中,符号int表示向下取整运算,符号%表示取余运算。
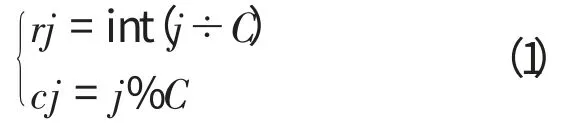
2 标定计算
2.1 有效剖分三角形区域的内插值线性关系不变性
图像采集系统的光学畸变会给标定图像带来非线性变形,其中,摄像机镜头的一阶径向畸变对图像中的非线性变形起到了主要作用,可以近似地认为图像非线性变形全部来自于摄像机镜头的一阶径向畸变[12~14],其数学模型,如式(2)所示。
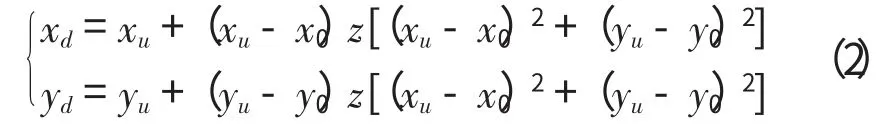
式中,(xu,yu)、(xd,yd)分别对应畸变前、后的像素坐标,(x0,y0)是畸变主点的像素坐标,z 为图像采集系统的一阶径向畸变系数。在完成像素坐标的提取后,按照图像坐标对特征点集P 进行Delaunay三角剖分,可以得到剖分三角形集合τ。由于图像非线性畸变的影响,τ 可能会包含对于本文所述标定计算起到干扰作用奇异剖分三角形,剔除这些三角形后得到的剩余有效剖分三角形集合存在一些有用性质。
2.1.1 有效剖分三角形的定义
对于有特征点集合按照图像坐标进行Delaunay三角剖分得到的剖分三角形集合τ,定义其中“顶点由一个特征点及其在特征点网格上的两个四邻域点组成的三角形”为有效剖分三角形。例如,图1(a)显示了一个3×3网格点集的Delaunay剖分三角形集合,图1(b)显示了其中的有效剖分三角形集合。
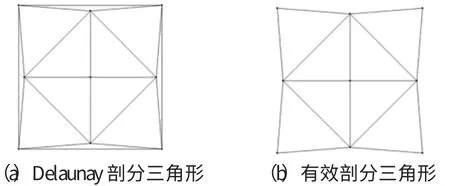
图1 有效剖分三角形定义示例
2.1.2 有效剖分三角形的建立
按照式(3)定义一个剖分三角形的形状偏差角η,其中,ω1、ω2、ω3分别为该三角形三个内角。
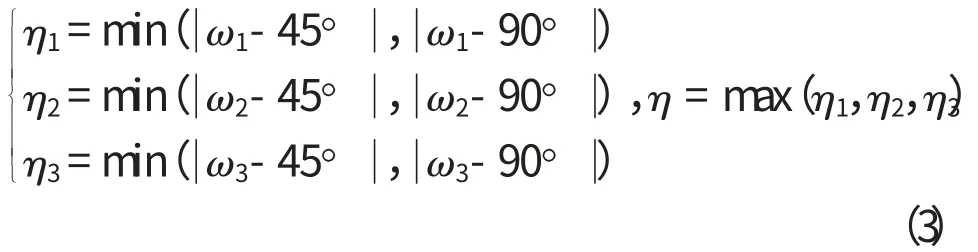
根据实际图像非线性变形程度设定合适的形状偏差角阈值η0(非线性变形越大,该阈值取得越高,取值范围一般在5°~25°),从三角形集合τ 中剔除其中η>η0的三角形可以得到有效剖分三角形集合τe。
2.1.3 有效剖分三角形的内插值精度分析
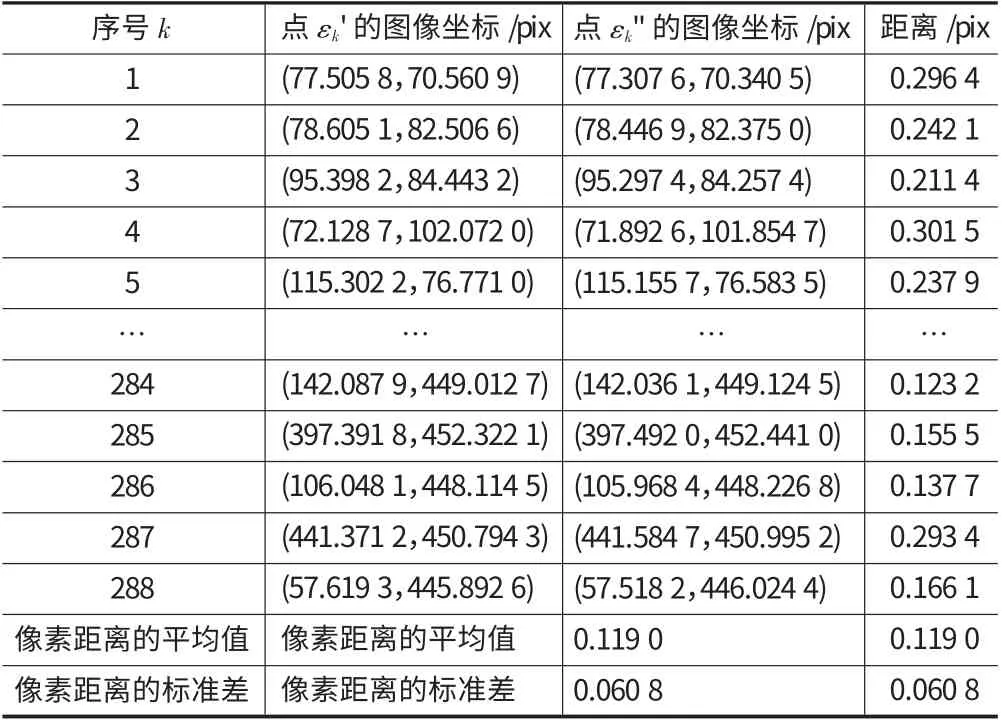
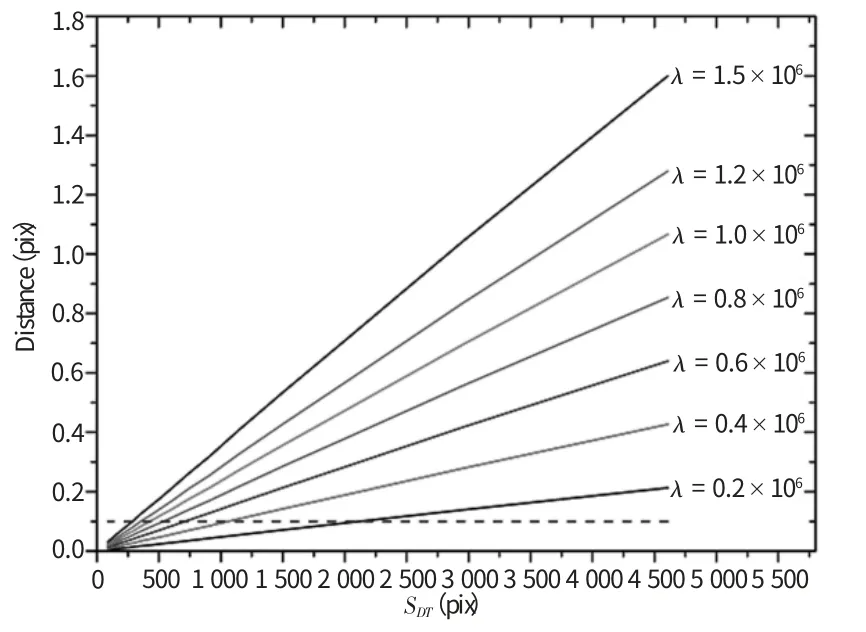
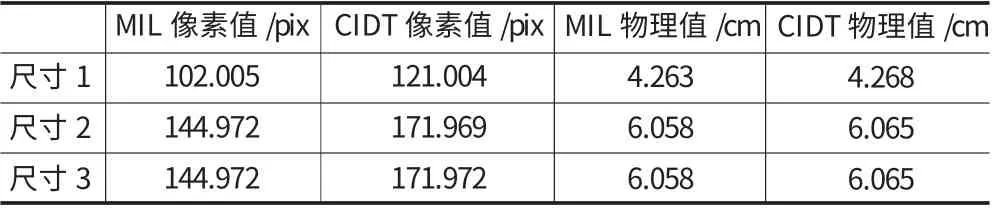
在大小为512×512的图像上,以像素点(64,64)为起点,以32为像素间距,均匀阵列分布着的13×13标准阵列点集合,记作ξ。对其进行Delaunay三角剖分并按照上述方法建立有效剖分三角形集合τ,如图2(a)所示。对τ 中的每个三角形τk(k 表示有效剖分三角形的序号)随机生成一组三角形内插值系数mk、nk(mk、nk应满足条件:0 图2 CDIT方法精度分析实验用仿真点集 按照式(2)对点集合ξ 和点集合ε 加入一阶径向畸变系数z=1×10-6的非线性畸变,得到变形后的点集合ξ'和ε',由ξ'亦可得到变形后的有效剖分三角形集合τ',结果如图2(c)所示。利用三角形集合τ'中的每个三角形τk'的顶点图像坐标按照与之前相同的插值系数mk、nk带入式(4)计算可以得到点集合ε",结果如图2(d)所示。对点集合ε'和点集合ε"中每对位于同一有效剖分三角形内的点εk'与εk",计算它们在图像上的像素距离,结果如表1所示(点个数太多,本文仅显示其中的一部分)。 表1 点集合ε'和ε"中对应点的像素距离 从表1可以发现,在畸变条件下,利用变形前像素点与其所在的有效剖分三角形顶点的内插值关系,由有效剖分三角形顶点插值估算得到的像素点位置与实际的像素点位置相差不大。对在大小为512×512的图像上以像素点(64,64)为起点的不同规格的标准阵列网格点集,分别加入不同程度的一阶径向畸变并按照上述方法计算实际像素点位置与内插值估算位置的像素距离,结果如图3所示。 图3 不同情况下实际位置与内插值估算位置的像素距离 可以看出,畸变程度越小,有效剖分三角形的面积越小(网格越密集),利用内插值估算出的像素点位置越精确。对于一副512×512图像而言,当阵列网格点的密度达到使得有效剖分三角形面积不大于250个像素时,即便畸变系数已经高达1.5×106(远远超过测量用图像采集系统最大畸变不超过1%的要求),这种估算的误差已经只有不到0.1个像素。 在实际应用过程中,只要阵列网格点足够密集,就可以认为由变形后的有效剖分三角形顶点按照变形前像素点与其所在的有效剖分三角形顶点的内插值关系估算得到的变形后像素点位置就是该像素点变形后实际的位置。这种在一定条件下,变形前后图像素点与其所在的有效剖分三角形顶点之间的内插值关系保持不变的性质,称作有效剖分三角形区域的内插值线性关系不变性。 根据2.1节中讨论的有效剖分三角形区域的内插值线性关系不变性,可以利用变形前每个像素点与其所在有效剖分三角形顶点的内插值关系,计算变形前每个图像像素点对应在变形后图像上的位置。将该对应关系以及变形前特征点的像素间距与特征点的物理间距存储起来,完成标定文件的制作。 2.2.1 变形前图像上特征点位置的估算 d=max((H+2)/(R-1),(W+2)/(C-1))(5) 设标定图像的高、宽分别为H、W,按照式(5)估算变形前特征点之间的像素间距d。并根据由用户输入的标定特征点物理间距D,计算得到坐标单位转换系数T=D/d。根据像素间距d,按照式(6)估算特征点网格最左上角点Plu在变形前对应点(记作Qlu)的图像坐标(XXlu,YYlu)。 根据点Qlu的图像坐标(XXlu,YYlu)与每个特征点Pi的网格坐标(ri,ci),按照式(7)计算变形前每个特征点Qi(此处i 的含义与1.2节提到的一致)的图像坐标(xxi,yyi)。按照这种方法估算得到的变形前特征点集,可以保证变形前图像每个像素点都被一个有效剖分三角形所包含。 2.2.2 内插值系数的计算 将有效剖分三角形集合τe中每个三角形△k(此处k 的含义2.1.3节一致)的顶点Pk1、Pk2、Pk3根据其对应的特征点序号i 按照式(1)计算其网格坐标,带入式(7)计算得到其对应的变形前点Qk1、Qk2、Qk3的图像坐标。从而得到△k对应的变形前三角形△k'。由△k'组成的三角形集合称为变形前的有效剖分三角形集合,记作τe'。 设变形前的标定图像为I',遍历I'的每一个像素点Bl(l 为图像像素点的顺序序号),在τe'中找到并记录包含Bl的三角形△k'(τe'中有且仅有一个三角形包含Bl)。设△k'顶点Qk1、Qk2、Qk3的图像坐标分别为(xxk1,yyk1)、(xxk2,yyk2)、(xxk3,yyk3),解 式(8)所 示 的二元一次方程组,得到三角形内插值系数ml、nl并分别存入WH×1矩阵M、N 的第l行中,其中(xxl,yyl)为像素点Bl的像素坐标。 2.2.3 变形前后像素点对应关系计算 遍历I'的每一个像素点Bl,根据Bl所在的三角形△k'的序号k 在三角形集合τe中找到三角形△k,设其顶点Pk1、Pk2、Pk3的图像坐标分别为(xk1,yk1)、(xk2,yk2)、(xk3,xk3);根据像素点序号l在矩阵M、N 中三角形内插值系数ml、nl。按照式(9)计算Bl在变形后图像I 中对应位置的图像坐标(xl,yl)。从而构建I'中每个像素点Bl对应在I 中对应位置的图像坐标映射关系“(xxl,yyl)→(xl,yl)”。 最后,将上述坐标映射关系与坐标单位转换系数T 一起存储到硬盘上,便完成了标定文件,便完成了标定文件的制作。综上所述标定文件的制作方法可以用如图4所示流程图来表示。 图4 标定文件的制作方法流程图 载入待处理图像II(II 与标定图像I 由相同的摄像机在相同条件下拍摄得到,其高度、宽度也分别为H、W)以及标定文件,创建一副高度H、宽度W 的空图像II',用于存放校正后的图像。遍历II'中每个像素点Fl',按照标定文件中存储的对应关系找到II'中每个像素点Ql'(xl',yl')变形后对应于图像II 的位置图像坐标(xl,yl)。用(xl,yl)的临近像素点Qllu(int(xl,),int(yl))、Qlld(int(xl,)+1,int(yl))、Qlru(int(xl,),int(yl)+1)、Qlrd(int(xl,)+1,int(yl)+1)的像素值pix(Qllu)、pix(Qlld)、pix(Qlru)、pix(Qlrd)(函数int()表示向下取整操作),双线性插值法得到像素点Ql'的像素值pix(Ql')。遍历结束后,II'中储存的就是图像II 通过校正后的理想图像。 读取标定文件中储存的坐标单位转换系数T,对于在II'计算得到的特征尺寸像素值,都可以通过乘以该系数的方式转换为世界坐标值。 图5(a)显示了一副存在较大非线性畸变的标定板图像,图5(b)显示了一副与图5(a)在相同条件(相同的摄像机、镜头、焦距、物距等)下拍摄得到的电路板图像。 图5 实验测试图像 已知上述标定图像中特征点间距的世界坐标值D=1mm,提取其中的特征点像素坐标并对特征点集合进行Delaunay三角剖分,以形状偏差角阈值η0=15°筛选有效剖分三角形,结果如图6所示。 图6 特征点集的有效剖分三角形集合 按照CIDT方法完成标定文件的制作并载入该标定文件对图5(a)、图5(b)所示的图像进行去畸变校正,结果分别如图7(a)、图7(b)所示。另外,利用图5(a)所示的标定图像采用成熟商用软件包MIL制作标定文件对图5(a)、图5(b)所示的图像进行去畸变校正,结果分别如图7(c)、图7(d)所示。可以看出,CIDT方法能够对存在较大程度畸变的图像达到良好的去畸变校正效果。由于在估计变形前的特征点分布时需要保证所有像素点都至少在一个有效剖分三角形内部,故CIDT方法校正图像会带来部分图像边缘区域信息损失的问题。一般而言,需要测量、定位的特征常位于图像中心,上述图像边缘区域信息损失可以忽略不计。 图7 MIL与CIDT方法分别得到的去畸变校正图像 采用CIDT方法与MIL软件包校正所得到的图7(b)与图7(d)中选择的3个特征尺寸,分别如图8(a)、8(b)所示。 图8 测试用特征尺寸 对这些特征尺寸都采用MIL软件包求取像素距离,并分别经过CIDT方法与MIL制作的标定文件转换为物理尺寸,结果见表2。可以发现,使用CIDT方法转换得到的特征尺寸物理值与通过MIL软件包转换得到结果差距可以保持在0.2%内。 表2 特征尺寸测试结果 (1)本文通过分析特征点集Delaunay剖分三角形的性质,定义了有效剖分三角形并提出了其筛选方法。同时,分析了有效剖分三角形区域的内插值线性关系不变性,利用这一性质提出一种新的平面标定方法,该方法采用分块线性插值代替了传统方法需要采用二元高次多项式拟合才能完成的变形前像素点与其在变形后图像上对应位置的映射运算,从而简化标定计算。 (2)测试结果表明,本文所述方法在应用于图像去畸变校正时,对于超出一般测量要求的非线性图像畸变仍然能有效去除。同时,该方法在校正图像的过程中也带来图像边缘信息损失的问题,当需要测量、定位的特征位于图像中心区域时,这一问题带来的影响不大。 (3)测试结果表明,本文所述方法在应用于图像坐标向世界坐标的转换时,精度与成熟商用软件包MIL相当,满足电子封装设备的精度要求。 [1]Li Junlan,Zhang Dawei,Zhao Xingyu,etal.Micro-vision positioning systems for IC packaging[J].Optics and Precision Engineering,2010,18(4):995-972. [2]Zhang Kai,Wang Yuhui,Yin Zhoupin.A fast vision alignment in high performance chipmounter[J].Optical Technique,2005,31(4):604-607. [3]Qiu Maolin,Ma Desong,Li Yi.Overview of Camera calibration forcomputervision[J].Acta Automatica Sinica,2000,26(1):43-55. [4]Zhang Guangjun.Machine vision[M].Beijing:Science Press,2005. [5]Zhao Xiaosong,Zhang Hongwei,Zhang Guoxiong,et al.Study on camera calibration technology[J].Chinese Journal of MechanicalEngineering,2002,38(3):149-151. [6]Liao Shizhong,Gao Peihuan,Su Yi,etal.A geometric rectificationmethod for lens camera[J].Journal of Image and Graphics,2000,5(7):593-596. [7]He Xiaolan,Jiang Guoquan,Du Shangfeng.Camera calibration arithmetic based on integration ofmultinomial[J].J.Cent.South Univ.(Science and Technology),2007,38(1):1117-1122. [8]LOWE D G.Distinctive image features from scale-invariant key-points[J].Pattern Recognition and Artificial Intelligence,2009,22(4):503-513. [9]Liu Ning,Lu Shengrong,Xia Ruixue,et al.Sub-pixel Harris corner detection algorithm based on Gaussian surfacemodel[J].Electronic MeasurementTechnology,2011,34(12):49-53. [10]Xia Ruixue,Lu Shengrong,Liu Ning.A Method of Automatic Extracting Feature Point Coordinates Based on Circle Array Target[J].China Mechanical Engineering,2010,21(16):1906-1910.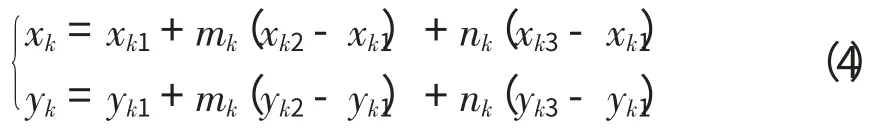

2.2 标定文件的制作

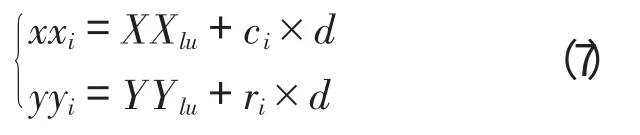
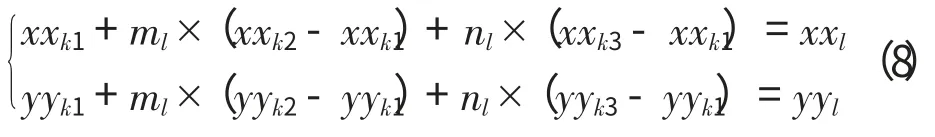
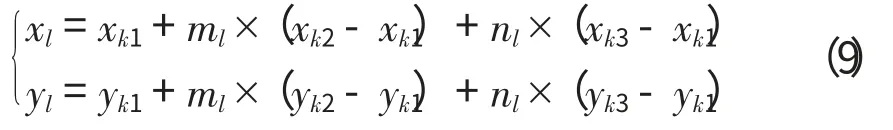
2.3 图像校正与坐标转换的实现
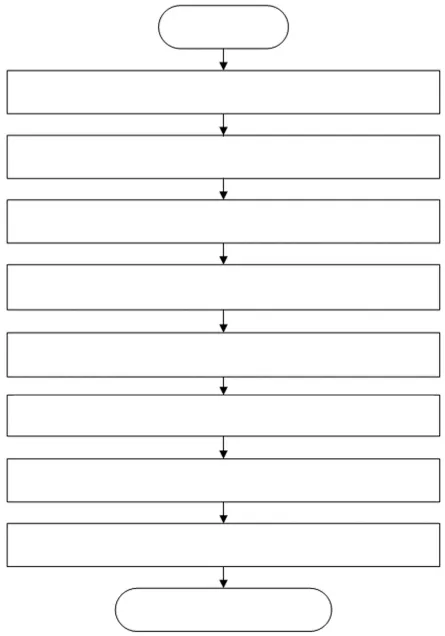
3 实验测试

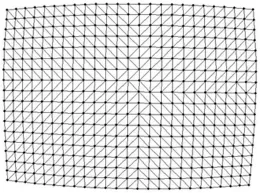


4 结束语

