制导炸弹串式联动增程弹翼运动特性①
王 焘,种艳艳,徐 超,袁隽琳
(1.西北工业大学 航天学院,西安 710072;2.武警工程大学,西安 710038)
0 引言
制导炸弹是在通用航空炸弹基础上加装制导装置和气动力控制面而制成的一类精确对地攻击武器。与普通航弹相比,它具有精度高、射程远和效费比高等突出优势,在近期几次局部战争中得到了广泛应用。采用滑翔弹翼是制导弹药增程、实现防区外远程精确打击、提高载机安全性的有效措施。串式联动折叠弹翼[1]最早是由欧洲武器制造公司MBDA依据连接翼的概念提出的一种新型滑翔增程折叠弹翼组件。它由靠近翼梢部铰接连接的前后翼条、可弹出弹翼的机械机构及飞行控制单元组成。发射前,前后翼条呈收拢折叠状态;发射后,前后翼条联动展开形成平面形状为菱形的桁架式连接翼构型。与单片滑翔弹翼相比,串式联动弹翼具有升阻比大、结构重量轻、承载特性好等突出优点,是目前美国联合攻击弹药(JDAM)和小弹径炸弹(SDB)增程的主要解决方案之一,也是未来极具潜力的制导航弹低成本化、模块化通用增程组件[2]。
在串式联动弹翼展开过程中,前后翼条协调联合动作。展开过程中的运动学参数是弹翼设计的重要技术指标。一些文献研究了串式联接弹翼的气动性能[3-4]、结构强度[5]、气动弹性[6]等问题,对运动特性方面的研究尚不多。本文针对串式联动弹翼的结构特点,研究其展开过程中重要运动参数的变化规律,深入掌握这类新型滑翔增程弹翼机构的运动特点,为进行串式联接弹翼的结构和机构设计及优化提供依据。
1 联动弹翼展开运动数学模型
某串式联动折叠弹翼由2个前翼条和2个后翼条构成。前翼条在翼根部与弹身铰接固定;后翼条根部铰接在弹出机构的运动滑块上,翼梢铰接固定在前翼条端部附近。展开时,作动机构驱动滑块沿导轨直线运动,依次带动后翼条、前翼条联动展开,直至到位锁定[7]。
1.1 联动机构的运动模型
根据串式联动折叠弹翼的工作原理,建立如图1所示的平面运动模型。坐标系原点位于后翼条驱动点初始位置,沿运动方向为x正向。图1中,虚线所示为弹翼折叠收拢状态位置,实线为展开过程中t时刻的位置;C为后翼条与滑块的铰接驱动点,A为前翼条与弹身的固定铰接点,B为前后翼梢的铰接点;δ为前翼条铰接点A与驱动轴之间的距离;d为前翼条铰接点与驱动点初始位置间的轴向距离;θ1、θ2分别为前后翼条的展开角,图示方向为正;x为t时刻驱动点的行程。
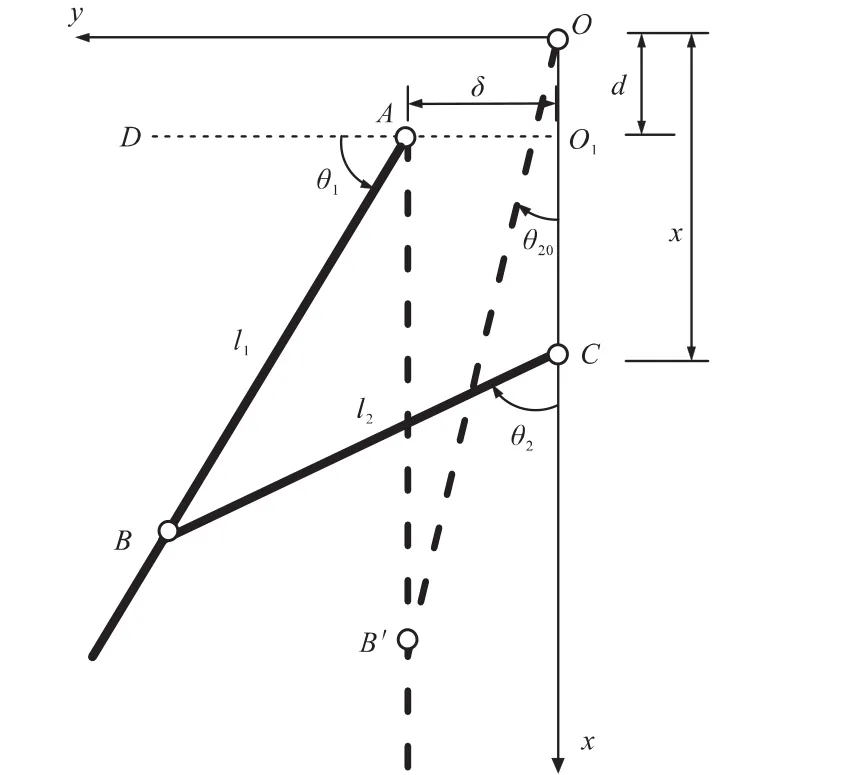
图1 串式联动弹翼运动模型Fig.1 Motion model of diamondback wing
1.2 折叠弹翼展开角与驱动速度的关系
对图1所示平面机构应用复矢量环路方程,可得
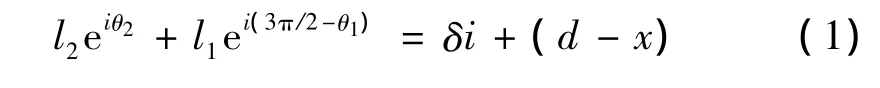

式(2)给出了前后翼条转角与滑块行程的关系。由式(3)求出Kθ和Kx,进一步可得折叠弹翼后翼条与滑块驱动点速度间的关系式为
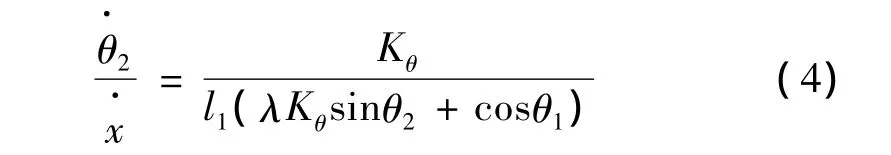
1.3 折叠弹翼展开角速度与驱动力的关系
取θ2为广义坐标,根据拉格朗日方程建立串式联动折叠弹翼的动力学微分方程。以图1所示机构为例,设m1、m2、m3依次为前翼条、后翼条和滑块的质量,Jb为后翼条对其质心的转动惯量;Jf为前翼条对A点的转动惯量;l21、l22分别为后翼条质心到B点、C点的距离。
1.3.1 系统的动能
系统的总动能为
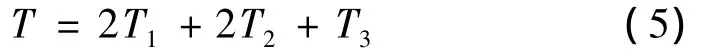
其中,前翼条的动能为

后翼条的动能为
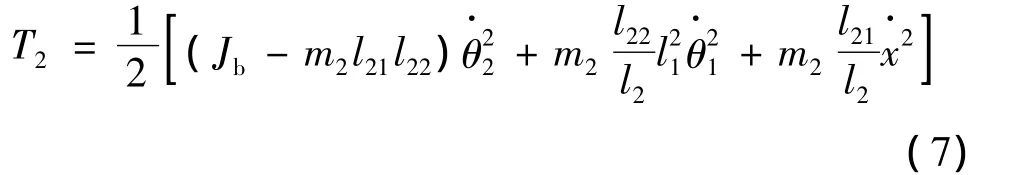
滑块的动能为

将代入式(5),则系统动能为

其中,系统广义惯量为
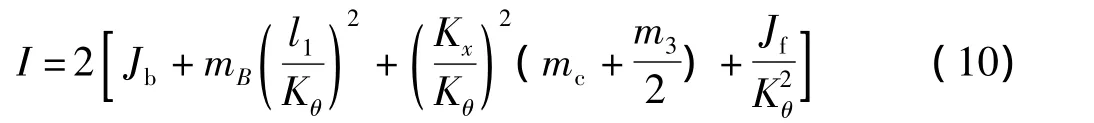
1.3.2 系统的广义惯性力
考虑作用在系统上的气动阻力和主动力,则作用在滑块上的推力功率为

气动阻尼矩M为

式中 Y为作用在翼面上的气动阻尼;xc为阻尼作用点到转轴的距离。
系统的广义惯性力为
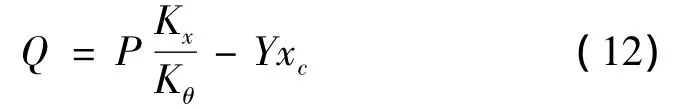
1.3.3 系统运动微分方程
根据理想约束系统的拉格朗日方程
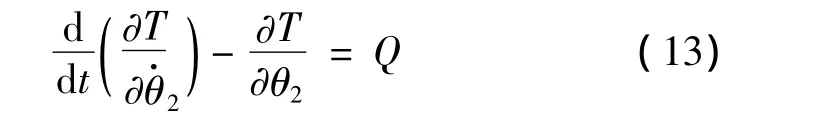
由式(10)知,广义惯量I是广义坐标θ2的函数,故
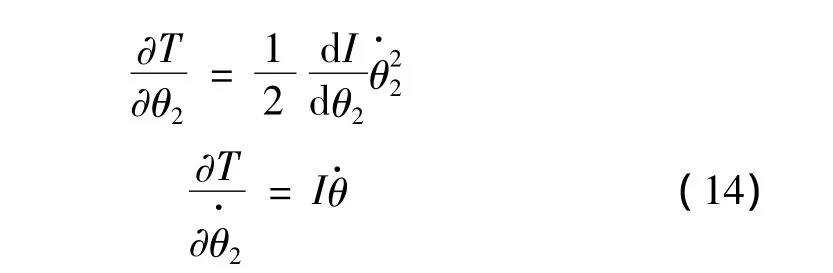

式(15)为非线性二阶常微分方程,给定初始条件后,可利用龙格-库塔法求得数值解,从而得到折叠弹翼展开角速度与驱动力的关系。
2 串式联动弹翼运动特性分析
设某串式联动弹翼前后翼条质量分布均匀。图1中,d=0.1 m,l1=1 m,δ=0.15 m。质量 m1、m2、m3分别为 6、6.6、0.33 kg。滑块上的额定推力为1 kN,后翼面运动转动至100°时,展开到位并被锁定。利用上文推导的运动数学模型进行求解,分析串式联动弹翼展开过程的运动特点。
2.1 前、后翼条转动角度及角速度运动规律
分别研究以下3种情况下的前、后翼条转角和角速度随时间变化的规律:
(1)滑块作速度为1 m/s的匀速运动;
(2)滑块作初速为零的匀加速运动,加速度取值保证展开时间与(1)相同;
(3)滑块受到额定推力驱动时。
分析结果如图2所示。由图2可知,不同的驱动运动模式下,前后翼条的转角和角速度运动规律也不同。匀速驱动下,后翼条转动角速度从较大初值快速减小,之后变化趋缓,转角快速到达展开角附近后,角度增大也变缓;对应前翼条的转角和角速度也先快速变化后逐渐趋缓。
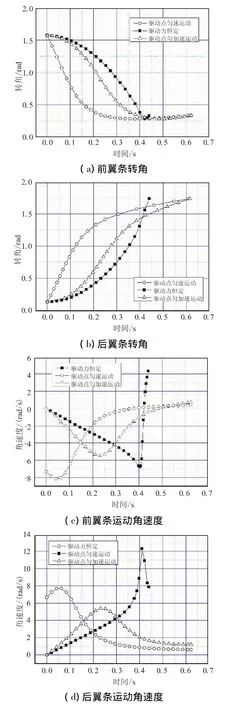
图2 前、后翼条转角及角速度运动规律Fig.2 Angle and angle velocity of wings variation vs time
以恒定推力作用于滑块时,前后翼条转动角速度均先以近似线性规律变化,表明此时角速度基本不变,但至后翼条展开角度为90°附近时,角速度变化非常剧烈。这是由于连接翼的构造特点,后翼条转动至90°位置时,前翼条转角达到极值,继续运动需要角加速度立即转向,因此角速度变化呈现冲击特征。过90°位置后,前后翼条角速度仍近似线性变化。滑块做匀加速度运动时,前后翼条的运动规律与恒定推力驱动情况下基本相同,但转动角速度和转角的运动变化规律则更为平缓,角速度变化没有明显的冲击现象,对结构造成的动过载明显减小。
综上可知,联动弹翼展开过程中,前后翼条的运动特性相仿;若控制滑块做初速度为零的匀加速运动,则可能得到运动特性较好的翼条运动规律。
2.2 不同翼条运动模式下滑块速度变化规律
考虑2.1节中的反问题,研究后翼条角速度变化规律已知情况下要求的驱动速度变化规律。研究以下3种情况:
(1)后翼条做角速度恒定运动;
(2)后翼条做初速为零的恒角加速度运动;
(3)后翼条角速度先匀速增大、后匀速减小时。
取值时,按照所有情况的展开时间都要求为0.44 s。图3给出了对应3种情况的驱动滑块运动速度变化规律。

图3 滑块驱动运动速度变化规律Fig.3 Driving motion velocity variation vs time
由图3可知,从展开到0.3 s附近,3种情况下滑块运动规律接近,驱动速度近似线性缓慢增加;但当后翼条运动至垂直于驱动轴时刻附近时,要求驱动速度快速变化,特别是(2)、(3)情况下,要求滑块速度急剧变化。因此,从作用实现和翼条展开运动控制的角度看,展开时间相同时,应尽量控制后翼条角速度做稳态缓变运动,此时要求的作动力较易实现。
3 联动弹翼结构设计参数影响分析
如图1所示,前翼条尺寸确定的前提下,结构设计参数δ、d不仅影响后翼条的尺寸,其对串式联动弹翼的展开运动特性也有重要影响。本文除对上述设计参数进行影响分析外,同时研究了不同驱动力下的机构运动特性。
3.1 δ、d的参数影响结果
研究额定推力P作用下,δ、d参数不同取值对机构展开时间、后翼条展开角速度的影响。图4给出了当 d=0.1 m,δ分别取 0.11、0.15、0.19 m 时,后翼条运动角速度的变化规律。图5给出了当δ=0.15 m,d分别取0.1、0、-0.1 m(负号表示图1 中 O1位于 x轴负轴上)时,后翼条运动角速度的变化规律。
各种情况下的展开时间列于表1。
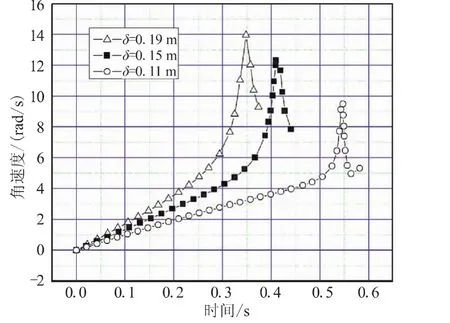
图4 δ参数变化对后翼条展开角速度的影响Fig.4 Expanding angle velocity of aft wing with different δ
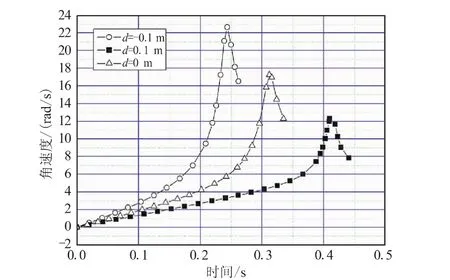
图5 d参数变化对后翼条展开角速度的影响Fig.5 Expanding angle velocity of aft wing with different d
3.2 不同驱动力的影响结果
图6给出了当恒定驱动力P分别取0.5、1、1.5 kN的情况下,后翼条展开角速度和系统动能的变化曲线。3种情况下的展开时间列于表1。
3.3 参数的综合影响分析
增大前翼条与弹身的固定铰接点与驱动轴之间的距离,联动弹翼展开时间缩短,后翼条角速度峰值和终值均增大。这是因为增大δ,实际上是后翼条长度增大,初始转角增大,因而展开所需时间缩短。改变前翼条与弹身的固定铰接点相对于滑块运动原点之间的轴向位置,O1位置越靠x负向,联动弹翼展开所需时间越短,后翼条的峰值和终值也越大。这是因为越靠负向,实际上是减小了后翼条长度,增大了后翼条初始转角。δ、d的参数影响分析表明,前翼条与弹身的固定铰接点与驱动轴和运动原点的相对位置对串式联动折叠弹翼的运动特性有重要影响,增大前翼条与弹身的固定铰接点与驱动轴的距离,或者使得该点位于运动原点之后,均能缩短展开时间,但运动过程中最大角速度以及到位时的冲击能量也增大。
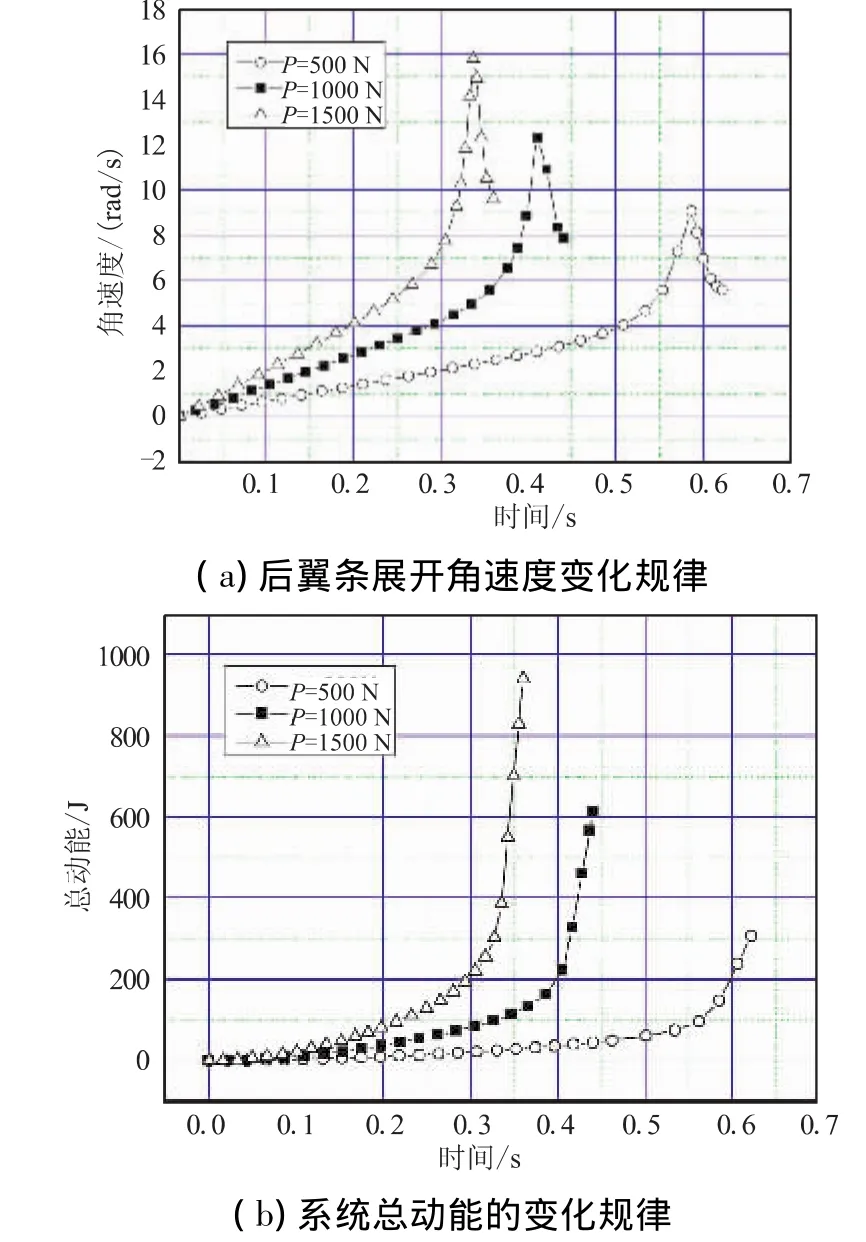
图6 驱动推力不同取值对系统性能的影响Fig.6 Expanding angle velocity of aft wing and total kinetic with different driving forces
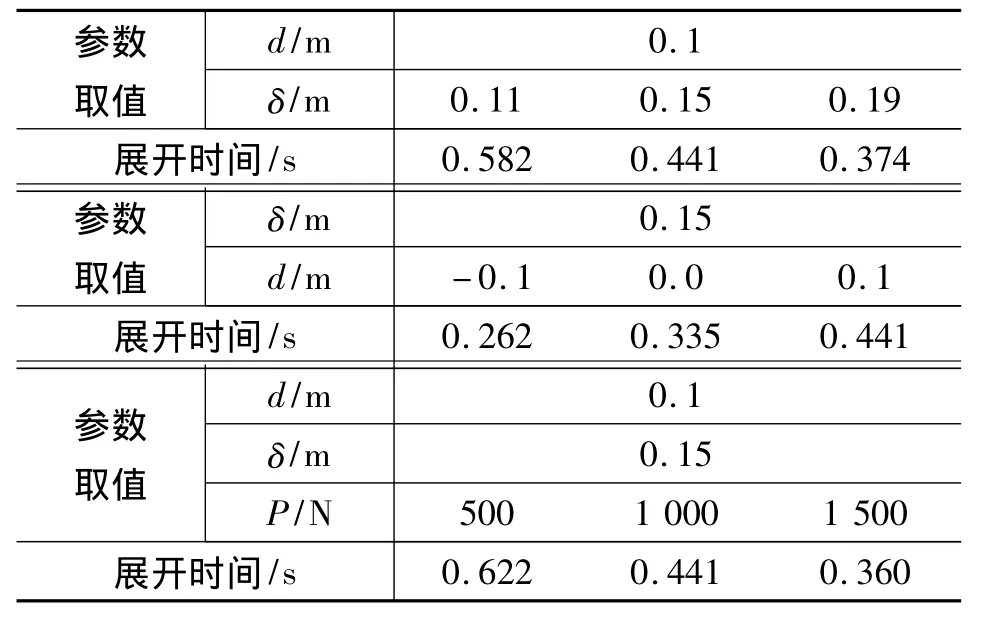
表1 不同参数取值下折叠翼展开时间比较Table 1 Results of time used to expand with different design parameters
单独增加驱动推力的大小,能够缩短展开时间。系统总动能的变化表明,后翼条运动至展开角90°附近时,系统动能快速增加,且驱动力越大,展开到位时刻,系统的总能量也越大。
4 动力学仿真
在对整个模型进行运动学分析后,很有必要进行动力学仿真,以研究系统在工作过程中各个部件的受力情况,以及系统在工作过程中不同部件之间是否存在干涉情况。
4.1 仿真模型
首先,在Solidworks建立系统的三维实体模型,如图7所示。

图7 三维实体模型Fig.7 3D model
根据确定的基本尺寸(d=0.1 m,δ=0.15 m)和推动模式(滑块匀速驱动),在MSC.ADAMS中建立动力学仿真模型进行仿真。所建立的模型如图8所示。
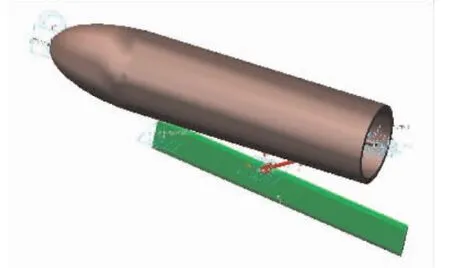
图8 动力学仿真模型Fig.8 Dynamics simulation model
模型中有弹身、弹翼、推力杆和推力滑块4个部件。其中,弹身和弹翼之间、推力杆和弹翼之间、推力滑块和推力杆之间都是通过旋转副连接;推力滑块和弹身之间通过水平滑移副连接。为了保证仿真结果的准确性,在这些运动副上都加入了摩擦。
4.2 仿真结果
模型仿真结果如图9所示。
从仿真结果和数值求解结果对比可知,所推导的理论计算方法正确,对于实际的制导炸弹串式联动弹翼设计具有非常重要的指导意义。
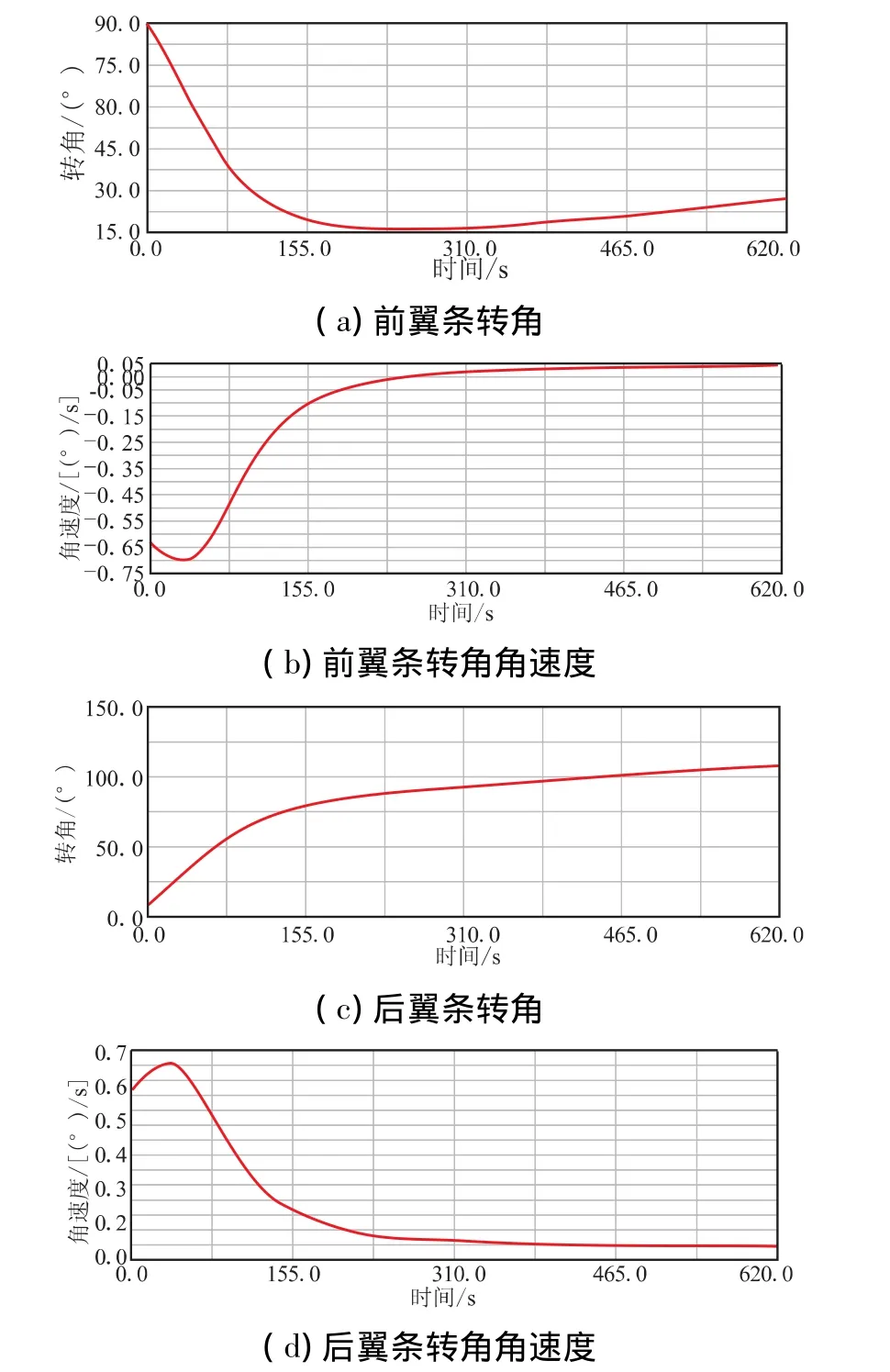
图9 模型仿真结果Fig.9 Simulation model results
5 结论
(1)基于运动学几何分析和拉格朗日动力学方程建模方法建立的运动数学模型,能描述串式联动折叠弹翼的运动规律。
(2)串式联动弹翼前后翼条在展开过程中运动规律接近,控制驱动点的运动速度规律是影响展开时间和冲击能量的主要因素。
(3)前翼条与弹身的固定铰接点与驱动轴和运动原点的相对位置,对串式联动折叠弹翼的运动特性有重要影响;基于动力学分析的设计结构参数优化,对提高机构性能有重要作用。
[1]Wolkovitch Julian.The joined wing:an overview[J].Journal of Aircraft,1986,23(3):161-178.
[2]吴甲生,雷娟棉.制导兵器气动布局发展趋势及有关气动力技术[J].北京理工大学学报,2003,23(6):665-670.
[3]雷娟棉,吴甲生.钻石背弹翼气动特性风洞实验研究[J].兵工学报,2007,28(7):893-897.
[4]Laurent Vieira D M.Aerodynamics of joined wing configurations[D].MSc thesis of Cranfield University,2006.
[5]Mary Fairchild Samuels.Structural weight comparison of a joined wing and a conventional wing[J].AIAA Journal,1982,19(6):485-491.
[6]Corneille J,Franke M E.Wind tunnel test of a joined-wing missile model[C]//In:38th Aerospace Sciences and Meeting & Exhibit,Reno,NV,2000.
[7]John D Shmoldas,et al.Extendable wing for guided missiles and munitions[P].US Patent,5615846,1997-4-1.

