基于EMD-Wavelet模型的实时交通流噪声数据清洗方法
赵海龙 张 干 吕安涛 姚 宁
(1.山东理工大学交通与车辆工程学院 淄博 255091;2.山东省枣庄市交通运输局 枣庄 277800;3.山东省交通科学研究所 济南 250031)
实现实时动态的智能运输系统是提高交通运输能力、改善交通运输环境和减少交通事故的关键,而准确稳定的交通流实时数据又是实现智能运输系统的基础,其中被污染的噪声数据严重影响了智能运输系统中交通状态辨识和交通事件检测质量[1-2]。传统的傅里叶变换在单分辨率上存在缺陷,小波变换法(wavelet)克服了这样的问题,但是面对非线性非平稳的交通流量数据,小波分析又显得力不从心[3],而在生物医学心电信号处理上兴起的经验模式分解法(EMD)可以很好地解决此问题[4]。本文汲取经验模式分解和小波变换各自的优点,构建了适用于实时交通流噪声数据清洗的 EMD-Wavelet组合模型[5-7]。
1 EMD-Wavelet去噪模型
1.1 去噪原理
1.1.1 EMD分解
经验模态分解(EMD)是对一个信号进行平稳化处理,将信号中不同尺度的波动或趋势逐级分解,产生一系列具有不同特征尺度的数据序列,每一个数据序列就是一个本征模态函数(IMF),使Hilbert变换得到的瞬时频率能够反映信号所蕴含的物理机理。
若给定信号x(t),则其EMD分解可写作以下形式

式中:cn(t)为经过第n次分解得到的IMF分量分解;rn(t)为分解后得到的残差。EMD分解过程不仅消除了模态波形的叠加,而且使波形的轮廓更加对称,其主要分解步骤如下:
(1)搜索信号中所有的局部极大值和极小值点,用三次样条曲线连接所有的局部极大值点形成上包络线,连接所有的极小值点形成下包线,并且确保信号x(t)上的所有数据点都在上下包络线之间。
(2)将上下包络线的均值记为m1,定义h1=x(t)-m1(1),若h1满足本征模态函数(IMF)的2个条件,则认为h1是分解得到的第一个IMF。
(3)若h1不满足本征模态函数(IMF)的条件,则将h1作为原始数据,重复步骤(1)和(2),直到得到满足条件的IMF,记第一个IMF分量为c1,则残量r1(t)=x(t)-c1(t)。
(4)再将rn作为原始数据重复以上过程,得到信号x(t)的n个满足IMF条件的分量。当rn成为常量或单调函数不能再从中提取满足IMF条件的分量时,循环结束。rn称为残余函数,代表信号的平均趋势。
1.1.2 小波去噪
一个含噪声的一维信号可表示为
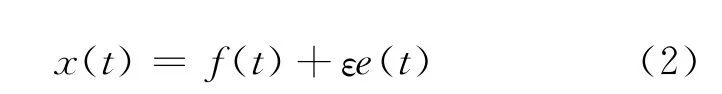
式中:f(t)为真实信号;e(t)为噪声信号;x(t)为含噪信号,ε为噪声水平。在实际工程中,有用信号f(t)通常表现为低频信号或较平稳的信号,而噪声信号通常表现为高频或非平稳的信号。小波去噪过程分为3个环节,具体步骤如下。
(1)小波分解。将信号f(t)变换到小波域,即小波变换。根据小波变换,分别计算不同尺度因子a和平移因子b组合时所对应的小波系数Wf(a,b)。
(2)阈值处理。在小波域进行滤波等信号处理,得到处理后的小波系数W′f(a,b)。这通常是小波分析的核心,大部分信号处理的过程都是在这一阶段完成的。
(3)小波重构。根据处理后的小波系数W′f(a,b)和小波逆变换公式(4),重构出原始信号f′(t),即小波反变换,达到消除噪声的目的。
1.2 EMD-Wavelet去噪步骤
(1)对原始交通量数据序列x(t)进行经验模式分解(EMD),得到n个IMF分量和一个残量R。
(2)根据累积均值指标辨别高频IMF分量和低频IMF分量,并选择合适的小波函数、分解层数和阈值对高频IMF分量逐一进行小波软阈值去噪。
(3)将去噪处理过的高频分量、未去噪处理的低频分量和残量进行EMD重构,得到干净稳定的交通量数据。
1.3 2个阈值的确定
EMD-Wavelet去噪模型实现的核心问题是2个阈值的确定:一个是EMD分解后高低频IMF分量的辨识阈值;另一个是小波变换时的阈值选择,这2个阈值选择准确与否,直接关系着噪声消除的效果,对数据清洗起着决定性的作用。
EMD分解后,为辨识高低频IMF分量,定义判别指标累计均值:
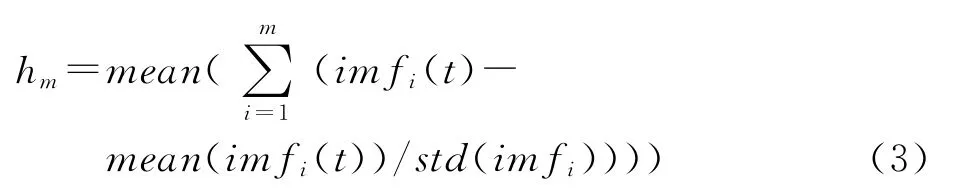
式中:imfi(i=1,2,…n)为原始信号x(t)的n个本征模态分量,且m≤n,若hm明显偏离零值,则认为从imfm开始是系统的趋势变化所致,所以可以判断:前m-1个IMF分量为高频分量,剩余的为低频分量。此时,只对高频IMF分量进行小波去噪即可。
小波消噪的阈值选择关系着噪声消除的质量,是小波变换的关键步骤。小波变换的阈值处理分为硬阈值和软阈值2种。
(1)硬阈值。它是把信号的绝对值与指定的阈值进行比较,小于阈值的点变为0,大于或等于阈值的点保持不变。在硬阈值处理过程中,得到的小波系数值连续性差,即ωλ在λ处是不连续的,重构得到的信号可能会产生一些震荡。
(2)软阈值。它是把信号的绝对值与指定的阈值进行比较,小于阈值的点变为0,大于或等于阈值的点变为该点值与阈值的差。软阈值方法中估计小波系数虽然整体连续性好,但是当小波系数较大时,ωλ和ω之间总存在恒定的偏差,造成了一定的高频信息损失,这将影响重构信号与真实信号的逼近程度,造成不可避免的误差。
硬阈值处理

软阈值处理
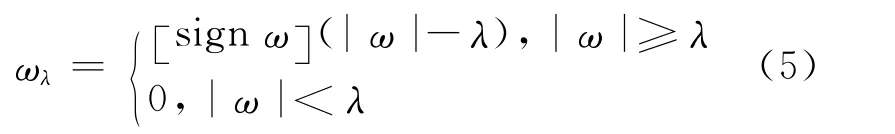
式中:ω为原始信号;λ为指定的阈值。一般情况,硬阈值比软阈值处理后的信号更粗糙些,并且硬阈值会有信号失真现象,所以一般选取软阈值处理。
2 实例分析
数据来源于2011年4月20日(星期三)淄博市金晶大道与联通路交叉口南进口左转车道的车流量,检测时间为07:00~19:00的连续12h,每5min检测1次,共检测到交通量样本数据144个,原始交通量数据见图1。从图1中可以看出,数据序列中有2个很明显的峰值和1个不太明显的峰值,反映出了一个正常工作日的交通量变化特点:在早上和晚上,由于上下班时间集中,车辆在短时间内迅速增加,所以分别出现了早高峰和晚高峰,且晚上回家时间较早上上班时间更宽裕,故晚高峰交通量变化幅度小且峰值时间长;而中午部分人选择回家,部分人不回家,所以稍微缓解了交通的压力,相对于早晚高峰交通量变化幅度小一些。

图1 原始交通量数据
借助于Matlab软件,首先对交通量样本数据序列进行EMD分解,得到4个IMF分量和1个残量,计算4个IMF分量的累计均值分别为h1=-0.111 7,h2=-0.229 3,h3=-0.326 7,h4=-0.122 4,根据累计均值和试算结果分析可知只有IMF1为高频分量,其余为低频分量;然后选择db1小波函数,对高频IMF1分量进行3层小波软阈值去噪处理;最后将去噪后的高频分量、低频分量和残量进行EMD重构,得到EMD-Wavelet去噪后的数据序列,并与单独使用EMD法和小波变换法去噪后的数据进行比较,见图2。

图2 EMD法、Wavelet法和EMDWavelet法去噪效果对比图
为了对比EMD去噪、小波去噪和EMDWavelet去噪的去噪效果,分别计算3种方法去噪的信噪比(SNR)和均方根差(RMSE)。信噪比反映信号噪声水平,SNR值越大,说明去噪效果越好。均方根差反映去噪后信号对原始信号的平均偏离程度,RMSE值越小,说明去噪后的信号与原始信号的相似度越高。3种方法的信噪比和均方根差见表1。
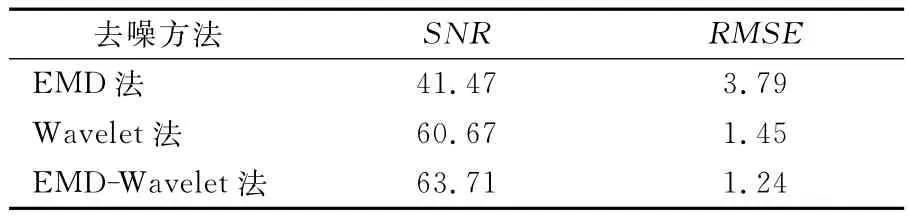
表1 EMD法、Wavelet法和EMDWavelet法去噪效果对比
实验结果表明:EMD-Wavelet法的去噪效果明显优于单独使用Wavelet法和EMD法,且Wavelet法的去噪效果明显优于EMD法。
分别对用以上3种方法去噪后的交通量序列及原始交通量序列建立灰色预测模型,由预测结果及相对误差可知,若对原始交通量序列去噪后再建立预测模型,则将获得更好的预测结果,且用EMD-Wavelet法去噪的交通量序列建立的预测模型其预测结果最好,预测效果明显优于单独使用Wavelet法和EMD法去噪后的交通量序列。实时交通量噪声数据的清洗提高了交通量预测的精度,也提升了智能运输系统中交通状态辨识和交通事件检测质量,同时为实现实时动态的智能运输系统提供了有力的基础保障。
3 结语
通过对经验模式分解理论和小波分析理论的阐述,并结合实例分析发现,EMD-Wavelet适合于分析非平稳非线性的数据序列,并且其去噪效果明显优于单独使用小波变换法和EMD法的去噪效果,为实时交通量的准确预测提供了技术支持。综上所述,EMD-Wavelet去噪方法是一种优越的方法,能够很好地应用于实时交通流噪声数据的清洗中去。
[1]陈淑燕,王 炜,李文勇.实时交通数据的噪声识别和消除方法[J].东南大学学报:自然科学版,2006,36(2):322-325.
[2]裴玉龙,马 骥.实时交通数据的筛选与恢复研究[J].土木工程学报,2003,36(7):78-83.
[3]王国华,窦慧丽,郭 敏.基于小波分析的交通数据自适应消噪算法研究[J].计算机应用与软件,2011,28(10):4-6.
[4]张泾周,寿国法,戴冠中.基于小波变换的心电信号噪声处理[J].西北工业大学学报,2005,23(1):11-14.
[5]赵玉玲,张兆江,姚习康,等.EMD-Wavelet降噪模型在动态变形数据处理中的应用[J].大地测量与地球动力学,2010,30(5):77-80.
[6]张道明,郝继飞,谭 国.基于经验模式分解的R波识别及噪声消除[J].计算机工程与设计,2007,28(1):217-223.
[7]赵志宏,杨绍普,申用军.一种改进的EMD降噪方法[J].振动与冲击,2009,28(12):35-38.

